基于Hilbert-Huang变换与理想带通滤波器的系统识别*

王其昂， 吴子燕， 刘 露

(西北工业大学力学与土木建筑学院 西安，710129)



基于Hilbert-Huang变换与理想带通滤波器的系统识别*

王其昂， 吴子燕， 刘 露

(西北工业大学力学与土木建筑学院 西安，710129)

针对经验模态分解存在模态混叠现象，提出基于Hilbert-Huang变换与理想带通滤波器的系统识别方法。该方法利用傅里叶变换得到结构加速度响应频响函数，粗略估计固有频率范围，通过半功率带宽法设计理想带通滤波器，定量化确定通带带宽，使信号在经过滤波器后频域内零相移，同时不改变其幅值谱。结构响应通过指定频带的理想带通滤波器产生若干窄带信号，利用经验模态分解获取结构模态响应，经Hilbert变换构造模态响应解析信号，并通过线性最小二乘拟合提取结构模态参数与物理参数。结果表明：半功率带宽法可实现带通滤波器频带的定量化设计,理想带通滤波器的零相移特点较好契合Hilbert-Huang变换用于系统识别的要求，两者结合可有效地解决模态混叠现象，减少虚假模态，大大提高结构系统识别精度。

系统识别; Hilbert-Huang变换; 理想带通滤波器; 经验模态分解; 半功率带宽法; 模态响应

引 言

工程结构系统识别与损伤诊断是结构健康检测的核心技术，处于该学科研究前沿。其首要任务是从测得数据中确定结构模态参数，从整体上描述系统动力特性，进一步辨识结构物理参数，为故障诊断、可靠性评估提供理论依据。

系统识别和损伤检测Benchmark模型在哥伦比亚大学UBC实验室建立[1]，并发展了卡尔曼滤波、小波变换、子空间识别等一系列方法[2-4]。小波变换[5-6]具有良好的时频分辨能力，避免傅里叶变换的Gibbs效应，利用时域脉冲响应提取结构模态参数，但其本质上为线性变换，不能有效处理非线性问题。基于经验模态分解(empirical mode decomposition, 简称EMD)的希尔伯特黄变换(Hilbert-Huang transform, 简称HHT)[7-8]，具有完全自适应性，不受Heisenberg测不准原理制约等优点，能处理非线性、非平稳信号。当结构两阶固有频率相似，基于Hilbert-Huang变换的模态参数识别较小波变换更为准确。但EMD方法存在模态混叠，限制了它在实际中的应用，其他学者提出改进的Hilbert-Huang方法[9-10]，利用傅里叶变换，估计固有频率范围，然后让信号通过指定频带的带通滤波器，改善模态混叠，但未涉及滤波器带宽定量化设计。 Yang等[11]利用Hilbert-Huang变换识别多自由度体系模态参数，并指出该方法用于系统识别中，带通滤波器相移应尽可能小。

由此，笔者提出基于Hilbert-Huang变换与理想带通滤波器的系统识别方法，利用傅里叶变换得到结构加速度频响函数，估计固有频率范围。为避免模态混叠，减少虚假模态响应，在使用EMD方法进行模态分解前，使信号通过指定频带的理想带通滤波器，将宽频信号分解为若干窄带信号。设计理想带通滤波器，使结构响应经滤波器后频域内零相移，同时不改变其幅值谱，并使用半功率带宽法定量化设计频带范围，减少模态混叠，提高结构系统识别精度。

1 脉冲激励下模态响应

多自由度系统外力作用下的动力学方程为

(1)

其中：X(t)=[x1,x2, …,xn]T为系统位移向量；M，C，K分别为质量、阻尼和刚度矩阵；p(t)为外部激励。

通过模态变换，位移、加速度响应分解为n阶实模态，考虑模态正交性可得

(2)

其中：ψj为第j阶模态向量；qj(t)为模态坐标；ωj，ζj和mj分别为第j阶模态频率、模态阻尼和模态质量。

若有以一激励作用在第r个自由度上，即当j=r时，pr(t)=p0δ(t)；当j≠r时，pj(t)=0。pj(t)为激励向量第j个元素。由此可知，第j个模态坐标下加速度响应为

(3)

因此，结构在第s(s= 1, 2, …,n)自由度上加速度脉冲响应可以表示为

(4)

(5)

(6)

其中：φsj,r为第j阶模态向量第s，r个元素相位差。

(7)

2 结构响应Hilbert-Huang变换

Hilbert-Huang变换[7]由EMD方法和Hilbert变换组成，其核心思想是将时间序列通过EMD分解成数个本征模函数(intrinsic mode function, 简称IMF)，之后利用Hilbert变换构造解析信号，计算得到信号瞬时频率和振幅。

2.1 EMD概述

EMD将一个复杂的信号分解为若干个IMF之和，每一个IMF均具有相同极值点与过零点数目，相邻零点之间仅一个极值点，且上下包络线关于时间轴对称。对于给定的信号x(t)(如加速度响应)，EMD基本步骤[7]如下：a.确定信号所有局部极值点;b.用三次样条曲线构造信号上(极大值点)、下(极小值点)包络线，分别为u(t)和l(t)；c.计算上下包络线的平均值，记为m1(t)，求出x(t)-m1(t)=h1(t)，若h1(t)满足IMF特性，即为第1个IMF分量;d. 若h1(t)不满足IMF的条件，则将其视为原始数据,重复步骤a～c，得到上下包络线平均值m11(t)，判断h11(t)=h1(t)-m11(t)是否满足IMF的条件，如不满足，则循环k次，得到h1k(t)=h1(k-1)(t)-m1k(t)，使得h1k(t)满足IMF的条件,记c1(t)=h1k(t)，为信号x(t)的第1个IMF分量;e.将c1(t)从x(t)中分离，得到r1(t)=x(t)-c1(t)，将r1(t)作为原始数据重复以上过程，直至分离出全部IMF，将x(t)分解为n个IMF与残余分量之和

(8)

2.2 半功率带宽法设计理想带通滤波器

为减少虚假模态，在使用EMD方法进行模态分解前，首先使信号通过不同频段的带通滤波器，将宽频信号分解为若干窄带信号。笔者设计了理想带通滤波器，使结构响应经滤波器后频域内零相移，同时不改变其幅值谱，提高模态参数识别精度。

理想带通滤波器具有完全平坦的通带，通带内没有放大或衰减，通带外频率被完全衰减，且通带外的转换在极小频率范围完成。具体设计思路如下：将加速度响应通过傅里叶变换得频响函数，通带范围内频响函数数据不变，通带外变为零，再通过逆傅里叶变换转化为时域数据，获得窄带加速度响应。根据半功率带宽法，保留信号峰值处多数能量，理想带通滤波器上、下限截止频率设计为幅值谱半功率点处，其带宽的功率谱密度比峰值低3 dB。

2.3 模态响应Hilbert变换及其解析信号

(9)

对于cj(t)的解析信号zj(t)为

(10)

其中：Aj(t)和θj(t)分别为IMF的瞬时振幅和瞬时相位。

(11)

(12)

由瞬时相位计算信号瞬时频率

(13)

信号瞬时振幅和瞬时相位均为时间函数。测量数据x(t)首先应用EMD分解成单一频率或窄带信号IMF，经Hilbert变换可得到有意义的结果，在任意时刻t仅有单一频率，使得瞬时频率具有实际物理意义。对于常规信号，瞬时频率随时间改变而非单一频率。

加速度模态响应由式(5)获得，其Hilbert变换可由Bedrosian定理计算

(14)

其中

(15)

(16)

由式(10)得模态响应解析信号为

(17)

若阻尼较小、固有频率较大，模态响应Hilbert变换式(14)简化为

(18)

瞬时幅值、瞬时相位公式简化为

(19)

(20)

3 系统识别

3.1 固有频率与阻尼比的识别

3.2 模态振型及物理参数识别

理论上固有频率、阻尼比的识别，仅需获取某一自由度上加速度响应,但对于模态振型、质量、刚度和阻尼矩阵的识别则需测得所有自由度上的响应。由式(6)可得到模态元素绝对值之比

(21)

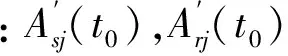
两模态元素相位差通过式(22)可得到

(22)

从式(21)和式(22)可以看出，将t0作为所取时间段的中间某点，得到θsj和θrj在t0处的拟合值，进而可以确定ψsj相对于ψrj的相位。根据式(7)，确定ψsj相对于ψrj符号(正或负)。由此，在j阶模态向量中的所有元素相对于某一特定元素的绝对值及符号都可确定。

得到模态参数后，结构质量、刚度和阻尼矩阵便可得到。将式(19)、式(20)带入式(6)中，第j阶模态质量为

(23)

其中:p0为可测冲击力荷载。

模态刚度ki、阻尼ci为

(24)

根据模态正交性得结构质量、刚度及阻尼阵为

(25)

其中:Φ为模态向量矩阵。

4 算例分析

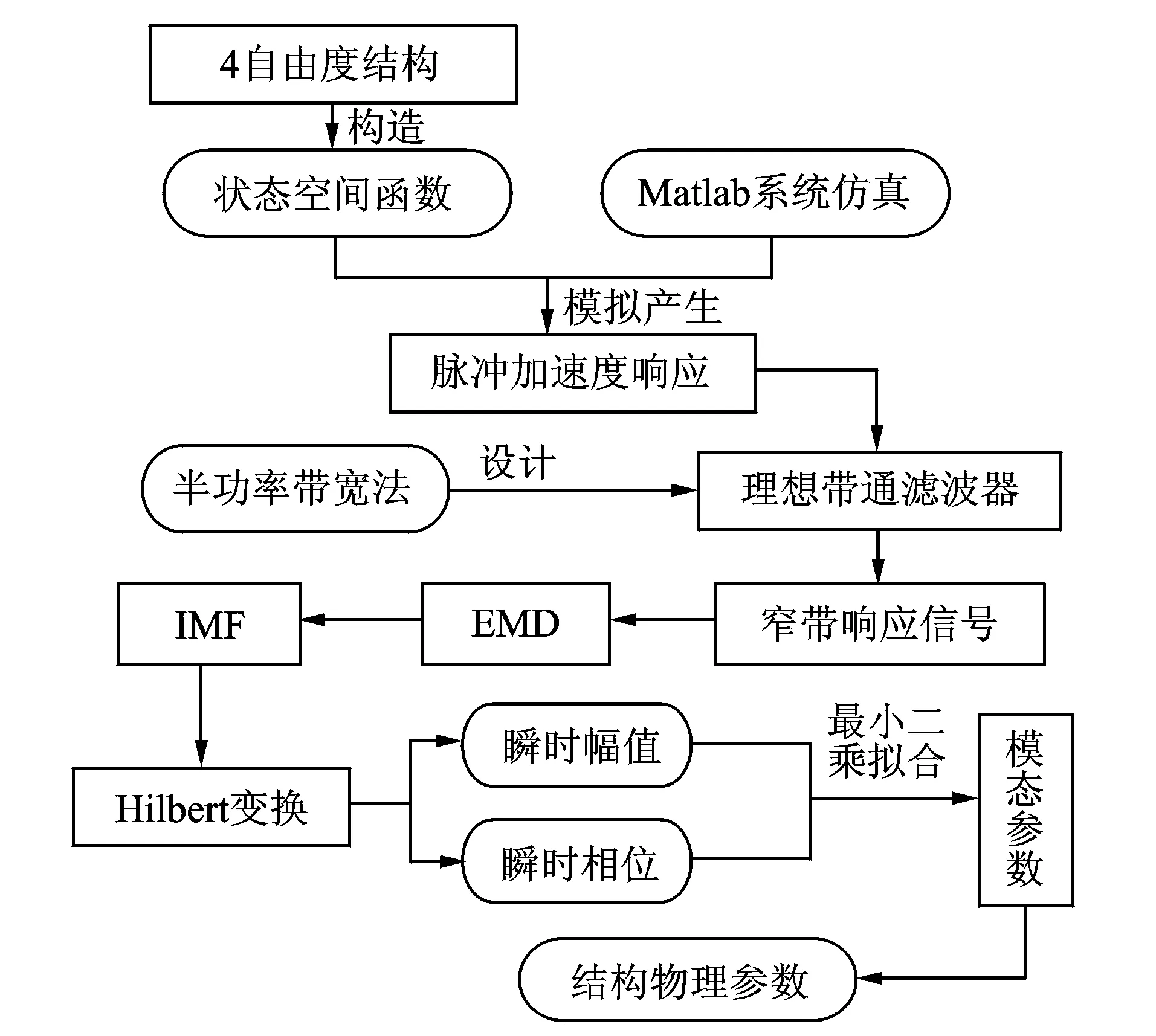
图1 结构系统识别流程图Fig.1 Flow chart for the structural system identification

图2 4自由度剪切梁模型Fig.2 Four degrees of freedom shear-beam structure

笔者以某4层剪切梁模型为算例，进行实验模态分析，并与理论分析结果作对比，以验证上述系统识别方法的有效性及准确性。具体流程见图 1。4层剪切梁模型见图 2，楼层质量均为4.989 5 kg，楼层刚度k1，k2，k3与k4分别为1 401，1 576，1 226与1 051 N/m，阻尼类型为瑞利阻尼。由质量矩阵和刚度矩阵按比例组合构造而成，质量比例系数Alpha为-0.001 6，刚度比例系数Beta为3.918 8×10-4。在第4楼层施加单位脉冲激励，构造系统状态空间函数公式。利用Matlab系统仿真获取各楼层加速度，而实际上任何实测数据都不可避免受到噪声信号的影响,因此本研究在响应信号中添加相同长度的高斯白噪声，信噪比为26.02 dB。

该系统4阶自振频率及对应阻尼比均可由任一楼层加速度脉冲响应获取。图 3为频域内加速度脉冲响应幅值谱，响应中主要包含4阶模态的振动成分，固有频率大致在0.925,2.475,3.85和4.95 Hz左右。

图3 脉冲响应频域幅值谱Fig.3 Frequency spectra of impulse responses

图4 带通滤波器相移图Fig.4 Phase shift of different band-pass filters

图5 4阶模态响应Fig.5 Four modal responses

图6 解析信号相位图Fig.6 Phase plot of the analytical signal

图7 解析信号幅值图Fig.7 Amplitude plot of the analytical signal

由固有频率和阻尼比识别步骤3得第1阶模态频率、阻尼。同时，对于其余3层响应可得第1阶模态响应，通过Hilbert-Huang变换理论计算可得第1阶模态参数，取均值得第1阶固有频率、阻尼比。重复同样步骤得其余3阶模态频率、阻尼比，并与Butterworth滤波器识别结果相比较，结果如表 1所示，由式(7)、式(21)确定模态向量。

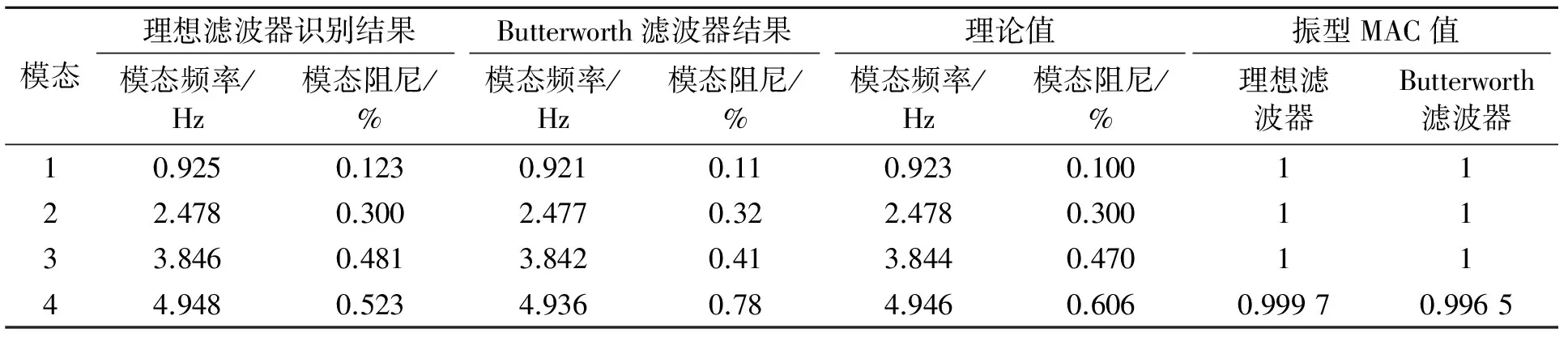
表1 结构模态参数识别结果

模态频率识别，两种滤波器估算结果一致，最大误差均小于0.2%。模态阻尼识别对数值误差较敏感，尚缺乏较为理想的识别方法，理想带通滤波器(最大误差23%)略优于Butterworth滤波器(最大误差28%)。模态向量识别结果与理论值相比得模态置信度(modal assurance criterion，简称MAC)值(见表 1)。4阶MAC值均大于0.99(实践中，两模态向量MAC值大于0.9时为强相关)，基于理想带通滤波器的识别结果与理论振型基本重合，模态向量识别精度高。

与常规Butterworth带通滤波器相比，理想带通滤波略提高模态参数识别精度。由于误差累积效应，这一提高对于结构物理参数的识别至关重要。1～4楼层质量识别结果分别为4.941，5.047，4.892和4.999kg，最大误差为1.95%，而Butterworth滤波器最大误差为11.83%。1～4楼层刚度识别结果分别为1 323.1，1 654.0，1 166.4和1 037.1，最大误差为5.56%，Butterworth滤波器最大误差为19.31%。阻尼矩阵主对角元素识别结果分别为Cd(1,1)=1.08，Cd(2,2)=0.98，Cd(3,3)=0.84，Cd(4,4)=0.41，最大误差为10%，常规滤波器识别结果误差为43.1%。为验证该方法识别灵敏度，在原有算例基础上分别修改质量、刚度矩阵。楼层质量修改为5.2 kg，以刚度识别结果为例，理想带通滤波器最大误差为3.7%，而Butterworth滤波器识别结果最大误差为11.4%。修改1～4楼层刚度，理想带通滤波器识别结果同样优于常规滤波器。由此，对于结构物理参数识别，理想带通滤波器处理后有明显优势，大大提高了识别精度。

5 结 论

1) 笔者提出基于改进的Hilbert-Huang变换的系统识别方法，利用傅里叶变换得到结构加速度频响函数，粗略估计固有频率范围。为减少虚假模态，使用EMD模态分解前，使信号通过指定频带的理想带通滤波器，将宽频信号分解为若干窄带信号，构造模态响应解析信号，提取模态参数与物理参数。

2) 理想带通滤波器的零相移特点较好契合Hilbert-Huang变换用于系统识别的要求，两者结合有效地解决了EMD中模态混叠问题。

3) 获取加速度响应幅值谱，由半功率带宽法，确定理想带通滤波器上、下限截止频率为幅值谱半功率点处，实现频带定量化设计。

4) 与常规Butterworth带通滤波器相比，理想带通滤波略微提高模态参数识别精度。但由于误差累积效应，这一提高对于结构物理参数的识别至关重要，大大提高了结构质量、刚度及阻尼矩阵的识别精度。

[1] Black C J, Ventura C E. Blind test on damage detection of a steel frame structure[C]∥Proceedings of SPIE. Santa Barbara CA: Society for Experimental Mechanics, 1998: 623-629.

[2] 任宜春，易伟建. 结构物理参数识别的多尺度参数卡尔曼滤波方法[J]. 工程力学，2008，25(5)：1-5.

Ren Yichun, Yi Weijian. Identification of physical parameters by multi-scale parameter Kalman filter[J]. Engineering Mechanics, 2008, 25(5): 1-5. (in Chinese)

[3] 史治宇，沈林. 基于小波方法的时变动力系统参数识别[J]. 振动、测试与诊断，2008，28(2): 108-112.

Shi Zhiyu, Shen Lin. Parameter identification of linear time-varying dynamical system based on wavelet method[J]. Journal of Vibration, Measurement & Diagnosis, 2008, 28(2): 108-112. (in Chinese)

[4] 徐良，江见鲸，过静珺. 随机子空间识别在悬索桥实验模态分析中的应用[J]. 工程力学，2002，19(4): 46-49.

Xu Liang, Jiang Jianjing, Guo Jingjun. Application of stochastic subspace method to experimental modal analysis of suspension bridges[J]. Engineering Mechanics, 2002, 19(4): 46-49. (in Chinese)

[5] Vafaei M, Alih S C, Abd Rahman A B, et al. A wavelet-based technique for damage quantification via mode shape decomposition[J]. Structure and Infrastructure Engineering, 2015, 11(7): 869-883.

[6] Dziedziech K, Staszewski W J, Uhl T. Wavelet-based modal analysis for time-variant systems[J]. Mechanical Systems and Signal Processing, 2015, 50-51: 323-337.

[7] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Oyal Society of London Proceedings, 1998, 454(1971): 903-995.

[8] Lee J, Hussain S H, Wang S, et al. Enhanced method to reconstruct mode shapes of continuous scanning measurements using the Hilbert Huang transform and the modal analysis method[J]. Review of Scientific Instruments, 2014, 85(9): 1-11.

[9] 付春，姜绍飞. 基于改进EMD-ICA的结构模态参数识别研究[J]. 工程力学，2013，30(10)：199-204.

Fu Chun, Jiang Shaofei. Study on the modal parameter identification based on improved EMD and independent component analysis[J]. Engineering Mechanics, 2013, 30(10): 199-204. (in Chinese)

[10]秦毅，秦树人，毛永芳. 改进的Hilbert-Huang变换在信号瞬态特征提取中的应用[J]. 振动与冲击， 2008，27(11)：129-133.

Qin Yi, Qin Shuren, Mao Yongfang. Application of improved Hilbert-Huang transform in transient feature extraction[J]. Journal of Vibration and Shock, 2008, 27(11): 129-133. (in Chinese)

[11]Yang J N, Lei Ying, Pan Shuwen, et al. System identification of linear structures based on Hilbert-Huang spectral analysis. part 1: normal modes[J]. Earthquake Engineering and Structural Dynamics, 2003, 32(9): 1443-1467.

[12]Shi Z Y, Law S S, Xua X. Identification of linear time-varying mdof dynamic systems from forced excitation using Hilbert transform and EMD method[J]. Journal of Sound and Vibration, 2009, 321(3-5): 572-589.

10.16450/j.cnki.issn.1004-6801.2016.06.005

*国家自然科学基金资助项目(51278420)；博士创新基金资助项目(CX201408)

2015-06-08；

2015-07-13

TB122; TB123

王其昂,男，1986年8月生，博士生。主要研究方向为结构健康检测、系统识别及可靠性评估。曾发表《Seismic fragility analysis of highway bridges considering multi-dimensional performance limit state》(《Earthquake Engineering and Engineering Vibration》2012,Vol.11,No.2)等论文。E-mail:qawang@mail.nwpu.edu.cn