阵列雷达波束内双目标的极大似然角度估计方法*

吴佳妮，陈永光，徐振海，熊子源，王雪松

(1. 国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073；2. 北京跟踪与通信技术研究所， 北京 100094)

阵列雷达波束内双目标的极大似然角度估计方法*

吴佳妮1，陈永光2，徐振海1，熊子源1，王雪松1

(1. 国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073；2. 北京跟踪与通信技术研究所， 北京 100094)

单波束内目标往往相距较近，采用传统角度分辨技术难以将其分辨，从而给目标跟踪和识别带来较大困难。于是提出基于LM算法的极大似然角度估计方法，实现波束内双目标的分辨。该方法在阵列雷达的基础上建立双目标回波模型，推导极大似然角度估计算法。考虑到求解算法直接影响极大似然角度估计的收敛速度和估计精度，利用LM算法实现了极大似然估计的求解，从而得到目标角度的精确估计。该方法避免了多次脉冲相干积累，具有计算量小的特点。仿真结果验证了方法的有效性。

单波束内双目标；极大似然估计；LM算法

传统的角度测量方法(如单脉冲法)主要针对波束内存在单个目标的情况，当两个或多个目标出现在同一波束内时，传统方法将不能对目标进行有效分辨，其角度估计结果往往与真实值差异较大。除引起角度测量误差外，不可分辨目标还会使得目标检测概率下降[1]。

为解决这一问题，有关学者在不可分辨目标的角度估计问题上展开了一系列深入的研究。Blair等[2-3]针对两个不可分辨的瑞利目标，利用单脉冲比实部和虚部的分布特性，提出了较完整的角度检测、估计的方法。Sinha等[4-5]基于单脉冲雷达，针对Swerling I与Swerling III型目标，提出了极大似然角度估计方法，该方法较文献[2]所述方法提高了估计精度，但在对似然函数解的搜索过程中，需要先验信息来排除一组错误的解。Wang等[6]在前文的基础上提出了联合信号到达角(Direction Of Arrival, DOA)估计，该方法结合了文献[2]中方法闭型解的简单形式以及文献[4]中极大似然估计方法精度较高的优点，但要求已知目标的信噪比。上述研究主要围绕改进的单脉冲技术展开，另一方面，基于阵列雷达，空间谱估计的方法对于实现目标的超分辨也具有较好的效果[7]。其中，多重信号分类(MUltiple SIgnal Classfication, MUSIC)算法与旋转不变技术信号参数估计(Estimation of Signal Parameters by Rotational Invariance Techniques, ESPRIT)算法是DOA估计中最常用的方法，围绕这两种方法，国内外学者提出了许多改进方法，如root-MUSIC，TLS-ESPRIT等[8]。

上述方法适用于以多次回波脉冲实现DOA估计，一些方法的估计性能与脉冲积累数密切相关[2-8]。为了提高角度估计性能，本文针对单波束内双目标问题，在阵列雷达的基础上，研究利用单次快拍信息实现目标角度估计的方法，以期在避免利用多次回波脉冲的同时，减少计算量。

1 双目标阵列雷达回波模型

考虑阵元数为N的均匀线阵，接收目标单次(快拍)回波的信号模型为：

x=A1s(u1)+A2s(u2)+n

(1)

其中：

2 极大似然角度估计算法

根据噪声的分布特性，接收信号的高斯密度函数为A1,A2,u1,u2的函数，其表达式为：

p(x;u,a)=

(2)

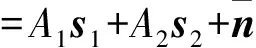
(3)

(4)

(5)

(6)

这些方程满足极大似然估计，由式(3)、式(4)可得：

(7)

(8)

3 Levenberg-Marquardt极大似然角度估计方法

LM算法是一种在非线性最小二乘问题中利用梯度求最小值的算法，它具有梯度法和牛顿迭代法的优点，同时克服了牛顿迭代法在应用中的一些限制[10-11]。牛顿迭代法具有局部二阶收敛性，收敛速度快。而LM算法仅利用一阶信息，获得近似牛顿迭代法的收敛速度，因而具有较优的收敛性能[12]。

g(ω)=Q(ω)=J(ω)TF(ω)

(9)

其中：J(ω)=F′(ω)=[F1(ω),…,FN(ω)]T，为F(ω)的Jacobi矩阵。

定义第k次迭代的搜索方向dk为：

(10)

其中：Jk=J(ωk),Fk=F(ωk),μk>0。

按照ωk+1=ωk+αkdk的迭代规则，产生迭代序列{ωk}，其中αk为步长因子。迭代序列的最后一个值即为最优化问题的解。

利用LM-ML角度估计算法估计角度的具体步骤如下所示。

步骤1：选取初始化的ω0值，即u10,u20，设定容许误差0≤ε≤1，最大迭代次数K，取μ0>0，设置k=0；

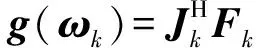
步骤3：求解dk，得到

步骤4：由Armijo搜索法确定步长因子αk；

步骤5：令ωk+1=ωk+αkdk，k=k+1，按式(11)更新μk的值，且将ωk+1代入式(7)、式(8)，更新A1,A2，转步骤2。

经多次迭代，最终输出满足条件的ωk(ωk=(u1k,u2k))，该值为LM-ML测角方法估计得到的两目标方位角的正弦值。注意到dk的取值是与μk相关的，实际上，在迭代过程中如何调整参数μk是LM方法的关键，其取值直接影响搜索方向角度，从而影响算法的收敛速度。依据参考文献[12]，设：

(11)

为说明LM-ML算法得到的估计值即为双目标角度的极大似然估计值，下面证明算法的收敛性。LM算法的收敛性定理[12]为：设{ωk}是LM算法产生的无穷迭代序列，若{ωk,μk}的某一聚点(ω*,μ*)满足J(ω*)TJ(ω*)+μ*I正定，则Q(ω*)=J(ω*)TF(ω*)=0，即ω*为极小值点。

(12)

J(ω)为N×2的矩阵。

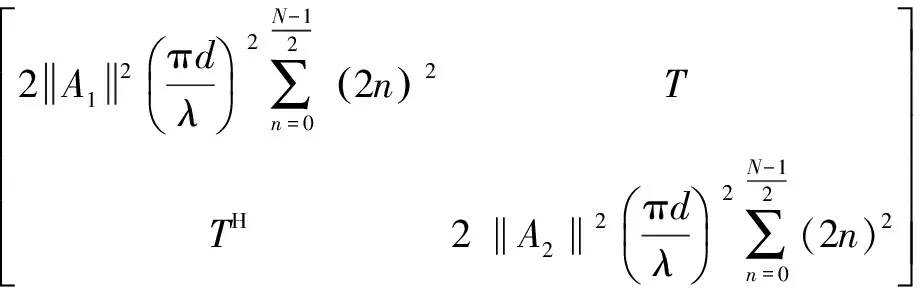
(13)

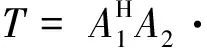
以上证明了LM-ML算法的全局收敛性。LM-ML算法引入最优化LM方法，可通过简单的计算得到双目标角度的极大似然估计。而极大似然估计为渐进无偏估计，可渐进达到克拉美-罗下限(Cramer-Rao Lower Bound, CRLB)[13]，因此通过分析CRLB，研究LM-ML算法的测角性能。

4 测角性能分析

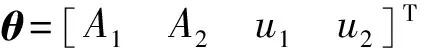
(14)

其中，γ(θ)=Sa，C(θ)=σ2I，

由CRLB(u)=[M-1(θ)]ii,i=3,4[14]得到：

{Re[(c⊙s)Hs]}2-{Im[(c⊙s)Hs]}2

(15)

值得注意的是，A1,A2为未知确定量，由文献[15]可知，此时的极大似然角度估计为角度的有效估计，其均方误差(Mean Square Error, MSE)由CRLB给出。

5 仿真实验

下面分情况讨论所提方法的收敛性能、角估计精度以及角分辨能力。分析收敛性能时将LM-ML算法与基于梯度下降法的ML(Gradient Descent based ML)算法[17]进行比较，而分析角度估计精度时与G-ML算法以及单次快拍MUSIC(Single snapshot MUSIC, S-MUSIC)算法[18]进行比较，以说明LM-ML方法具有收敛速度快，测角性能好的优点。在研究某一因素对测角性能影响时，固定其他参数为典型值。为分析统计性能，进行Monte Carlo仿真，各实验的仿真次数均为1000。

5.1 收敛性能仿真分析

5.1.1 收敛性与信噪比的关系

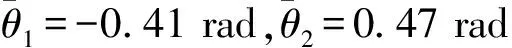
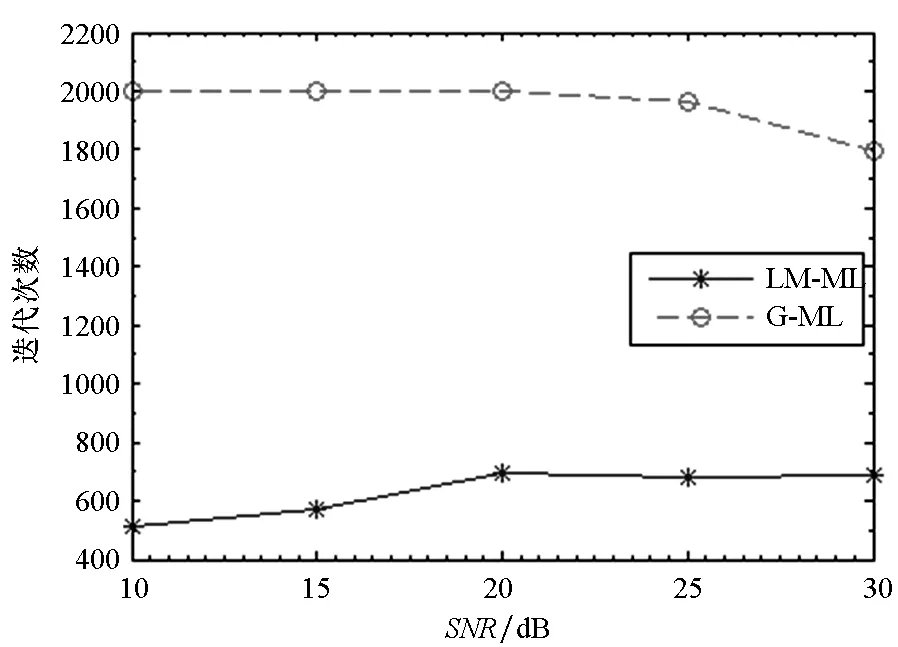
图1 两种方法的迭代次数与SNR的关系曲线Fig.1 Iteration numbers of G-ML and LM-ML for different SNR

由图1可见，LM-ML角估计方法的迭代次数远小于G-ML角估计方法，说明LM-ML能较快收敛。而G-ML角估计方法在SNR<25 dB时，迭代次数为最大迭代次数，即在容许误差ε=10-8，最大迭代次数K=2000的条件下，该方法不能收敛。

5.1.2 收敛性与两目标夹角的关系

本实验中，设定SNR1=SNR2=30 dB，图2给出了两种方法的迭代次数随目标夹角的变化关系。

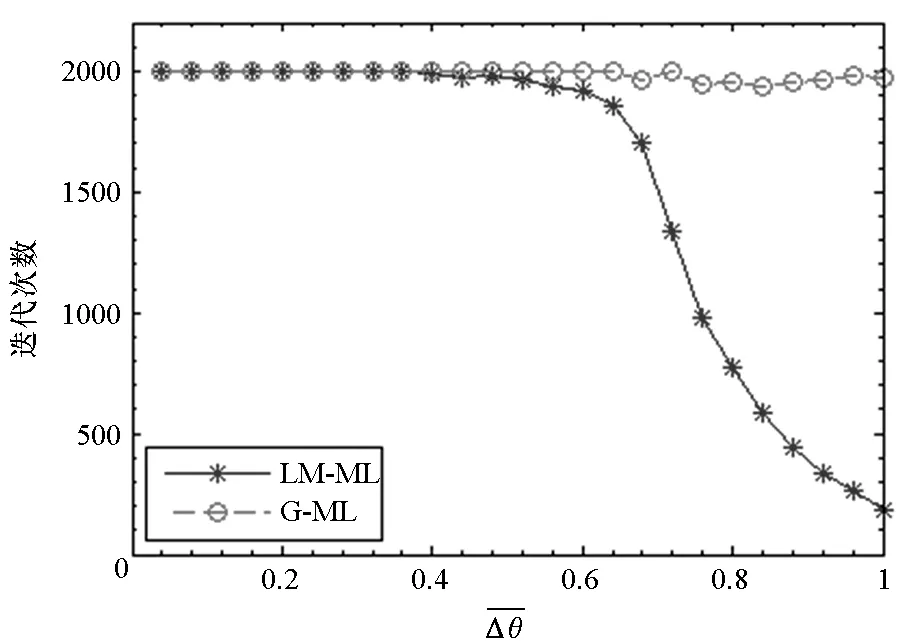
图2 G-ML和LM-ML方法的迭代次数与的关系曲线Fig.2 Iteration numbers of G-ML and LM-ML for different inter-target angle

由图2可见，当目标间隔小于0.4倍波束宽度时，两方法在迭代2000次时均未达到收敛条件，而间隔大于0.4倍波束宽度后，LM-ML方法的迭代次数随着两目标夹角的增大显著下降。可见，LM-ML方法具有更好的收敛性能。

5.2 角度估计精度仿真分析

5.2.1 测角精度与信噪比的关系

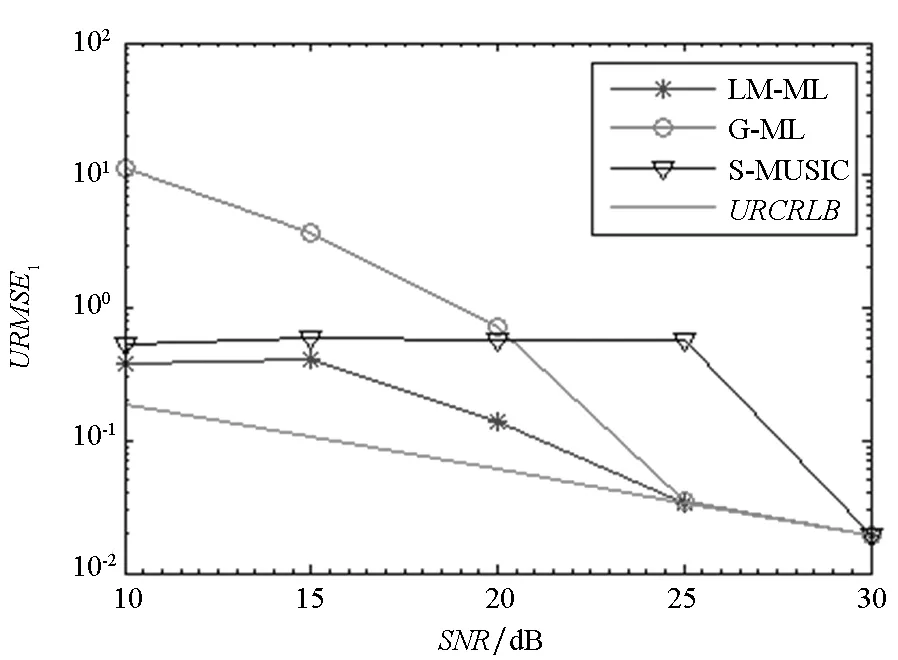
图3 三种方法的URMSE1与SNR的关系曲线Fig.3 URMSE derived from three methods for different SNR

从图3看出，随着信噪比的提高，URCRLB降低，LM-ML方法在SNR>25 dB时，达到URCRLB。S-MUSIC算法均方根误差相对较大，而G-ML方法在SNR<25 dB时，角度估计误差较大，测角精度较低。可见这两种方法的抗噪性能较差。

5.2.2 测角精度与两目标夹角的关系

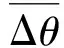
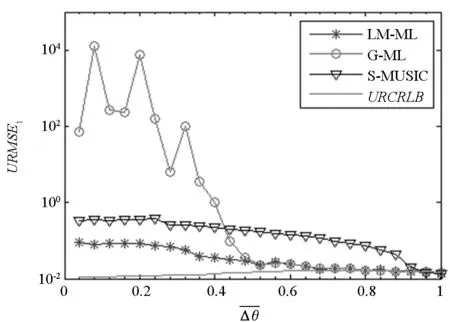
图4 三种方法的URMSE1与的关系曲线Fig.4 URMSE1 derived from three methods for different

由图4可见，URCRLB对目标的夹角敏感，而随着目标夹角的增加，三种方法的测角的均方根误差先后达到URCRLB。G-ML估计方法在目标间隔小于0.5倍波束宽度时，测角误差急剧增大，且小于0.4倍波束宽度时，URMSE1>1，此时该方法不可用。而S-MUSIC算法在小于0.9倍波束宽度时，测角误差显著增大。相较而言，LM-ML角估计方法随夹角的变化起伏较小，具有较高的测角精度。

通过以上实验对LM-ML方法与G-ML方法的对比可知，不同数值求解方法不仅直接决定角度估计算法收敛速度，同时还影响角度的测量精度。

5.2.3 幅相误差对测角精度的影响

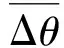
图5 幅相误差对URMSE1的影响Fig.5 Relationship between amplitude and phase errors and URMSE1

图5中，幅相误差为-40 dB时，目标1的角度估计精度与无幅相误差时相近；幅相误差为-30 dB时，均方根误差小幅增加。由此可见，LM-ML算法具有较好的稳健性。

5.3 角度分辨力仿真分析

本实验分析了LM-ML算法的角度分辨能力，设定目标估计的均方根误差小于0.2倍目标角度间隔时，目标为有效分辨。图6给出了不同幅相误差条件下，算法可分辨两目标的角度间隔的相对波束宽度随信噪比变化的曲线。

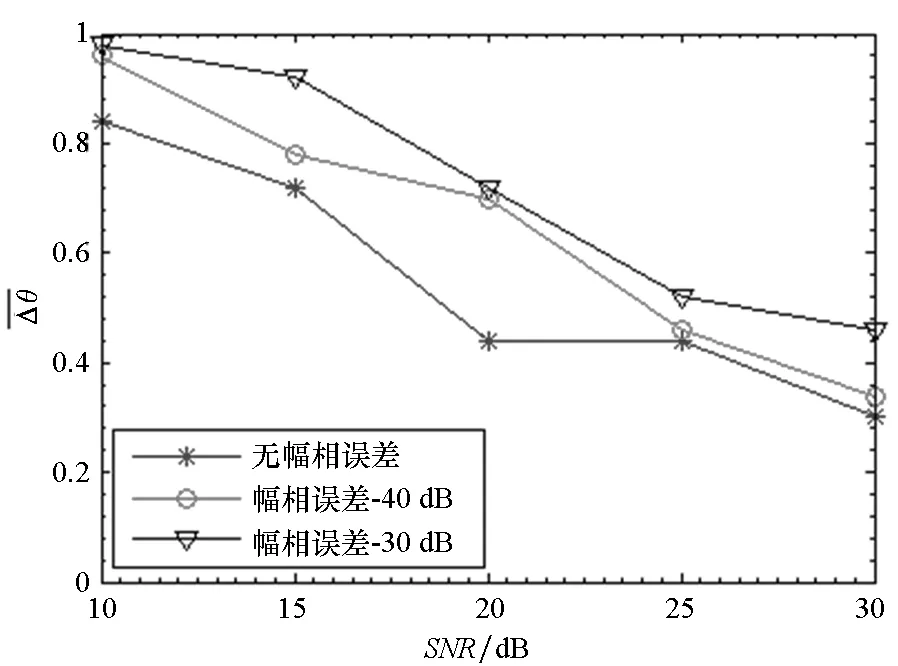
图6 角度分辨力与SNR的关系曲线Fig.6 Resolution of LM-ML for different SNR

由图6可见，随信噪比的增加，算法的角度分辨能力增强。而加入幅相误差，算法分辨力有所下降，且在信噪比较低时，幅相误差对分辨力的影响更为显著。

6 结论

本文在阵列雷达基础上，针对单波束内存在双目标的情况展开研究。根据阵列雷达回波特点，建立了双目标回波模型，得到了基于极大似然原理的角度估计方法。随后研究了极大似然估计的数值求解方法，提出了一种基于LM算法的角度求解方法。仿真实验表明，LM-ML算法具有收敛速度快，测角性能好的优点，能够对单波束内的双目标角度进行精确估计，从而实现不可分辨目标的角度分辨。

References)

[1] Sherman S M. Monopulse principles and techniques[M]. USA: Artech House, 1984.

[2] Blair W D, Brandt-Pearce M. Monopulse DOA estimation of two unresolved rayleigh targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 2(37): 452-469.

[3] Blair W D, Brandt-Pearce M. Statistical description of monopulse parameters for tracking Rayleigh targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 2(34): 597-611.

[4] Sinha A, Kirubarajan T, Bar-Shalom Y. Maximum likelihood angle extractor for two closely spaced targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 1(38): 183-203.

[5] Sinha A, Kirubarajan T, Bar-Shalom Y. Tracker and signal processing for the benchmark problem with unresolved targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 1(42): 279-300.

[6] Wang Z, Sinha A, Willett P, et al. Angle estimation for two unresolved targets with monopulse radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 3(40): 998-1019.

[7] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004. WANG Yongliang, CHEN Hui, PENG Yingning, et al. Space spectral estimation theory and algorithms[M]. Beijing:Tsinghua University Press, 2004.(in Chinese)

[8] 张小飞, 汪飞, 徐大专. 阵列信号处理的理论和应用[M].北京: 国防工业出版社, 2010. ZHANG Xiaofei, WANG Fei, XU Dazhuan. Theory and algorithms of array signal processing[M]. Beijing: National Defense Industry Press, 2010.(in Chinese)

[9] White W D. Low-angle radar tracking in the presence of multipath[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 835-852.

[10] Ranganathan A. The Levenberg-Marquardt algorithm[J]. Tutorial on LM Algorithm， 2004, 11(1): 101-110.

[11] Wilamowski B M, Yu H. Improved computation for Levenberg-Marquardt training[J]. IEEE Transactions on Neural Networks, 2010, 21(6): 930-937.

[12] 马昌凤. 最优化方法及其MATLAB程序设计[M]. 北京: 科学出版社, 2010. MA Changfeng. Optimization method and the MATLAB programming[M]. Beijing: Science Press, 2010.(in Chinese)

[13] Kay S M. Fundamentals of statistical signal processing, estimation theory[M].USA: Prentice-Hall, 1993.

[14] Stoica P, Larsson E G, Gershman A B. The stochastic CRB for array processing a textbook derivation[J]. IEEE Signal Processing Letters, 2001, 8(5): 148-151.

[15] Farina A, Gini F, Greco M. DOA estimation by exploiting the amplitude modulation induced by antenna scanning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 4(38): 1268-1276.

[16] 苏卫民, 顾红, 倪晋麟, 等. 通道幅相误差条件下MUSIC空域谱的统计性能[J]. 电子学报, 2000, 28(5): 105-107． SU Weimin, GU Hong, NI Jinlin, et al. A statistical performance analysis of the MUSIC algorithm in the presence of amplitude and phase perturbation[J]. ACTA Electronica Sinica, 2000, 28(5): 105-107.(in Chinese)

[17] Bianchi N C, Krogh A, Warmuth M K. Bounds on approximate steepest descent for likelihood maximization in exponential families[J]. IEEE Transaction on Information Theory， 1994， 40(4): 1215-1218.

[18] Ren Q S, Willis A J. Extending MUSIC to single snapshot and on line direction finding applications[C]// Proceedings of IEE Radar 97, 1997: 783-787.

Maximum likelihood angle estimation of two targets with array radar

WU Jiani1, CHEN Yongguang2, XU Zhenhai1, XIONG Ziyuan1, WANG Xuesong1

(1. State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System,National University of Defense Technology, Changsha 410073, China;2. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China)

As the targets in the same beam are close to each other, it is difficult to resolve them via traditional techniques. Furthermore， it also brings difficulty in detecting and tracking. The problem of resoling two targets in the same beam was studied with array radar. An echo model of two unresolved targets with array radar was established. An improved angle estimation method was proposed based on the maximum likelihood estimation principle. In consideration of the convergence speed and estimation accuracy, the Levenberg-Marquardt method was applied to obtain the maximum likelihood estimation of target direction. The simulation results prove that the method performs well in several aspects, including smaller estimation error and computational cost.

two targets in the same beam; maximum likelihood estimation; Levenberg-Marquardt method

10.11887/j.cn.201606021

2015-05-17

国家自然科学基金资助项目(61401488，61490694)；国家863计划资助项目(2013AA122202)

吴佳妮(1988—)，女，湖南醴陵人，博士研究生，E-mail：tuotuonini@163.com； 徐振海(通信作者)，男，研究员，博士，硕士生导师，E-mail：drxzh930@sina.com

TN95

A

1001-2486(2016)06-130-06

http://journal.nudt.edu.cn