衰落信道下基于正交频率码分复用的精确时间测量*

高 凯，朱 江，邹建彬，张 炜，周资伟

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

衰落信道下基于正交频率码分复用的精确时间测量*

高 凯，朱 江，邹建彬，张 炜，周资伟

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

针对衰落信道下的精确时间测量，给出基于正交频率码分复用技术的高精度时间测量算法。在不降低最大不模糊时间的前提下，通过时间延时、信道衰落、相位噪声参数的联合迭代估计，有效克服了频率选择性信道的衰落与相位噪声对时间测量的影响。仿真结果表明：联合迭代算法提高了时间测量的归一化均方根误差性能。

正交频率码分复用；分集；扩频；时间测量

正交频率码分复用(Orthogonal Frequency and Code Division Multiplexing，OFCDM)系统利用时、频域的二维扩频能够显著提升系统的性能，其在抗干扰通信与隐蔽通信等领域具有很强的优势[1-5]。无线电波传播时延的精确测量通常可基于载波相位的测量实现，雷达领域的多频测距(测相)技术与OFCDM技术相结合可在不降低最大不模糊时间的条件下，有效地提高测量性能。

针对分布式相参干扰节点之间高精度同步，文献[6]提出了一种基于OFCDM的高精度时间测量方法，利用时频域的二维扩频，实现信号的二维分集合并，显著提高了系统的时间测量精度。但是该文仅针对加性高斯白噪声(Additive White Gaussian Noise，AWGN)信道，未考虑衰落信道以及信道的相位噪声对测量精度的影响。在衰落信道下以及考虑相位噪声的条件下该算法的性能会显著下降。

文献[7-9]主要考虑了正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统的相位噪声，分析了相位噪声对系统性能的影响，给出了考虑相位噪声条件下OFDM系统的迭代同步算法，但是未涉及精确时间测量。本文提出一种新的联合迭代精确时间测量算法，综合考虑信道的衰落与相位噪声对性能的影响，实现了相位噪声、信道衰落、时间同步误差的联合估计，该算法有效提高了时间的测量精度。

1 系统模型

无线衰落信道中的考虑相位噪声的OFCDM系统模型如图1所示。系统假设具有1个导频码信道，K-1个数据码信道，导频码信道主要用于精确时间的测量，数据码信道用于信息比特的传输，分别采用不同二维扩频码进行扩频，K个信道采用码分多址复用后，再采用常规的OFDM调制与解调结构。假设二维扩频码时域扩频因子为NT，频域扩频因子为NF。

发射端，经二维扩频以及复用后的数据，先经过M点的快速傅里叶逆变换(Inverse Fast Fourier Transform，IFFT)模块，再插入循环前缀后得到一个OFCDM符号的采样数据，最后再变频到载频fc发射。假设每一帧发送NT个OFCDM符号，则其等效的复基带信号可表示为：

(1)

其中，Sm,i(t)与Sp,m,i(t)分别是通信与导频信号在第i个OFCDM符号的第m个子载波上的等效基带信号。

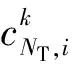
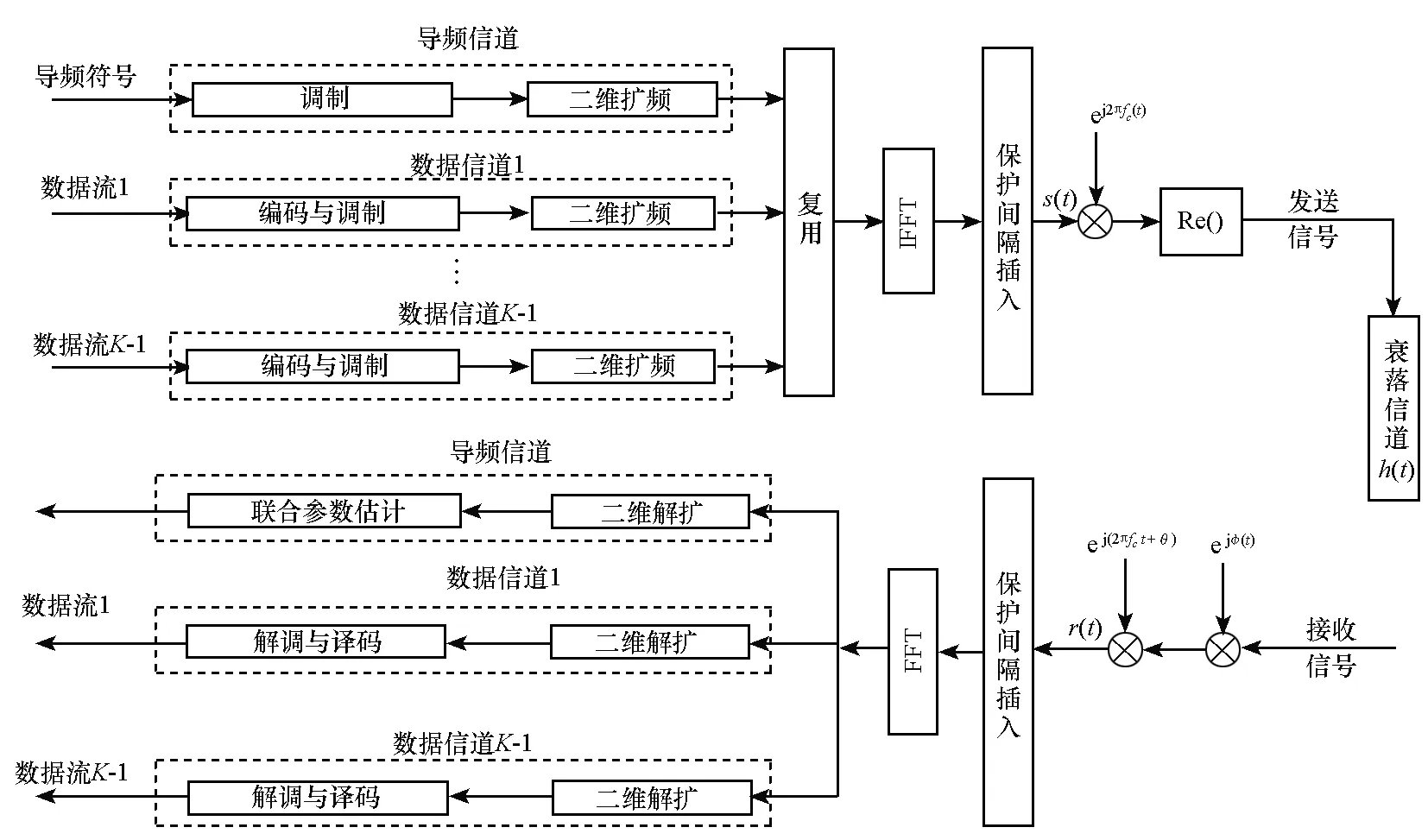
图1 OFCDM系统模型Fig.1 System model of OFCDM

发射后的信号经过衰落信道的传输后，在接收端进行下变频，可得到相应的基带信号。

r(t)=ejφ(t)[S(t)*h(t)]+v(t)

(2)

其中，φ(t)为相位噪声，h(t)为衰落信道的等效脉冲响应，v(t)为AWGN，*代表卷积。

经过采样、去除循环前缀以及快速傅里叶变换(Fast Fourier Transform，FFT)后，可获得第i个OFCDM符号第m个子载波上对应的等效基带信号为：

(3)

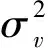
(4)

考虑到扩频码中导频码信道的扩频码与其他数据信道的扩频码之间良好的正交特性，导频码信道与数据信道的数据可被有效地分离出来。为分析方便，下文只考虑yi(m)中与导频码信道相关的部分。

OFCDM系统可采用时域与频域的二维扩频提高时间测量的准确性。经过时域解扩之后，第m个子载波上的等效基带信号可表示为：

(5)

用矩阵可表示为：

(6)

其中，

H=diag[H0,H1,…,HM-1]

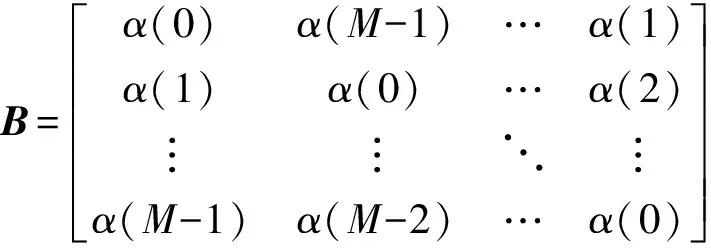
(7)

(8)

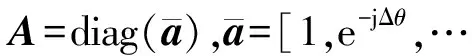
AWGN信道中，信道传输矩阵H退化为单位矩阵；不考虑相位噪声时相位噪声矩阵B也退化为单位矩阵。

2 同步算法

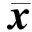
H，B分别具有M个未知参数，则共有2M+1个未知参数需要联合估计。从式(6)中只能获得M个样值，显然根据信号估计理论，无法直接估计出2M+1个未知参数。采用适当的建模方法，降低传输矩阵H与相位噪声矩阵B的维数，以解决上述问题。

2.1 估计参数降维

假设衰落信道的时域脉冲响应hn的长度为L，则其频域响应可表示为：

显然，信道传输矩阵可通过估计hn获得，信道的未知参数由M个降为L个。Hm与hn之间的关系如式(9)所示。

(9)

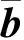
(10)

则，根据式(4)、式(10)可得:

(11)

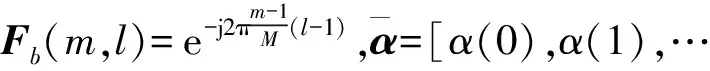
2.2 迭代估计算法

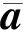
步骤4：根据估计出的Δθ与式(8)，计算矩阵A的估计值。

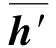
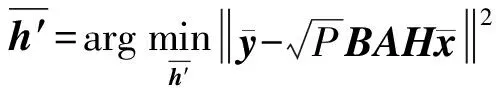
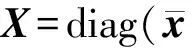
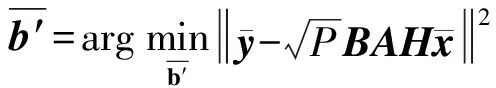
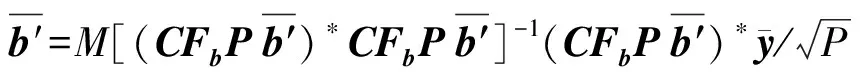
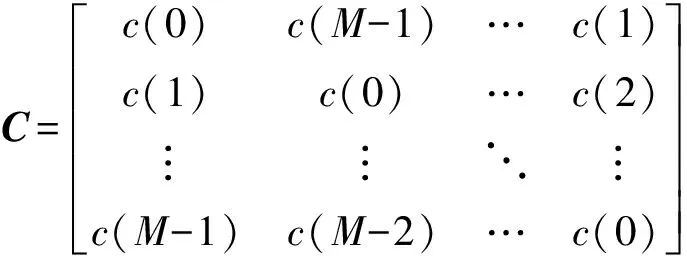
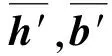
3 性能分析与数值仿真

3.1 性能分析

时域解扩后，式(5)可重新写为：

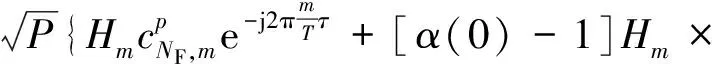
(12)

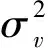
不采取信道衰落与相位噪声的补偿，则式(12)中第一项是期望信号，其余项为噪声，接收信号的信噪比为：

(13)

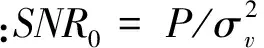
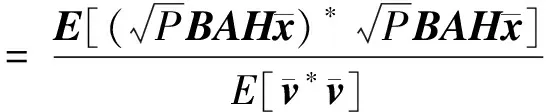
(14)

文献[11-12]给出了加性高斯白噪声信道下，时间测量的最大不模糊值τunamb=1/Δf，Δf=fm1-fm0为求相位差时所使用的载波的频率间隔。使用相邻载波求相位差，故最大不模糊时间为T，1/T=fm+1-fm。文献[6]给出了加性高斯白噪声信道下，时间测量的归一化均方根误差(Root Mean Square Error，RMSE)为：

(15)

将式(13)、式(14)中的结果代入式(15)，可求出不补偿以及理想补偿条件的时间测量精度。从表达式可知，不补偿时具有很大的测量损失。提出的算法，可提高时间测量的精度。迭代算法的信噪比推导非常复杂，3.2节将通过仿真来验证算法的性能。

3.2 数值仿真

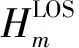
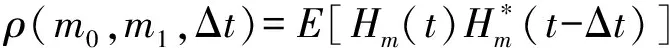
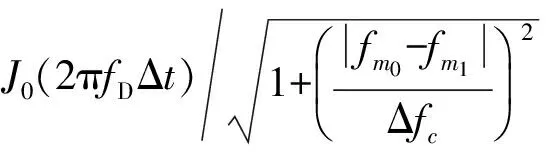
其中，fD是信道的最大多普勒扩展；Δfc是信道相关带宽；fm0-fm1第m0与第m1子载波的频率间隔；J0(·)是零阶的第一类贝塞尔函数;Δt是时间间隔。

基于维纳模型对相位噪声进行仿真，相位噪声ejφ(t)的自相关函数以及单边带相位噪声功率谱密度[14]分别为：

其中，v为频综的等效滤波器带宽。

仿真时，基于文献[15]中的方法对Rician衰落信道进行仿真。仿真中循环前缀的长度为64；衰落信道脉冲响应的长度L为32；相位噪声估计时取N为64；频域扩频因子NF与OFCDM子载波数M相同。

接下来分别仿真了不同相位噪声的参数、不同Ricain因子K、不同的信道多普勒扩展以及不同的频率选择性信道相关带宽Δfc情况下，采用联合补偿(Joint Compensation, JC)算法进行时间参数估计的性能，并与没有采用补偿(No Compensation, NC)、理想补偿(Ideal Compensation, IC)的性能进行了对比。

图2 不同v值条件下时间参数估计的RMSEFig.2 RMSE of time delay with the different v

图2仿真了不同相位噪声参数下，联合迭代测量算法在不同的信噪比条件下的性能。仿真中Ricain因子K为0 dB、信道相关带宽Δfc为1 MHz、多普勒扩展参数fDT为0.1、时域扩频因子NT为8、频域扩频因子NF为256。图3仿真了算法在不同的Rician因子与信噪比条件下的性能。仿真中相位噪声参数为200 Hz，其他参数同上文。图4仿真了不同的信道多普勒扩展条件下算法的性能。仿真中相位噪声参数v为200 Hz、K为0 dB、信道相关带宽Δfc为1 MHz，其他参数同上文。图5仿真了不同相关带宽Δfc对迭代算法性能的影响。仿真中fDT为0.1，v为200 Hz，K为0 dB，NT为8、NF为256。

显然，由图2～5可知：①不采用信道衰落与相噪补偿时，时间测量的精度在大于一定的信噪比后有显著的恶化，无法随着信噪比的提高而加大；②采用迭代算法后，在一定的信噪比范围内，相对不补偿的方法，性能可提高一个数量级。

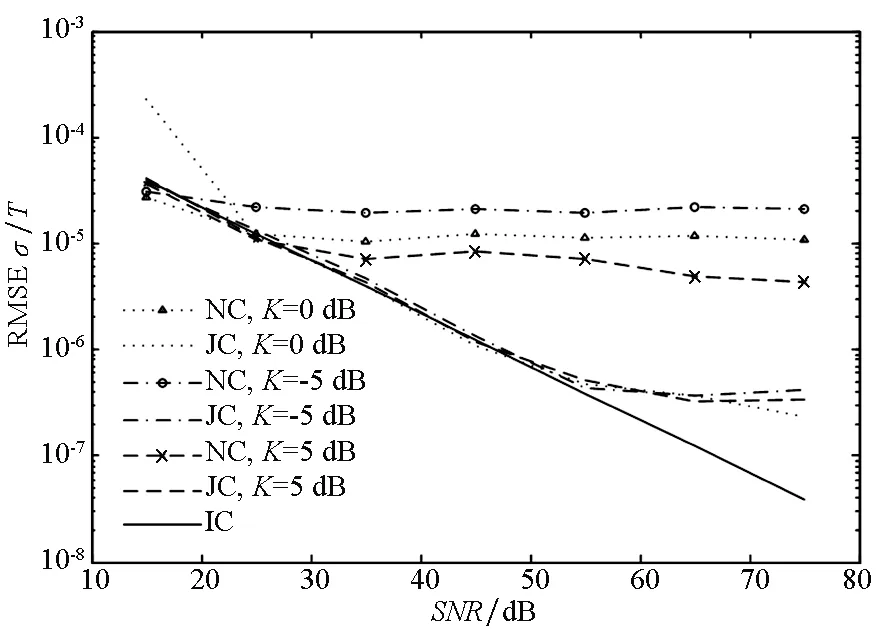
图3 不同K值条件下时间参数估计的RMSEFig.3 RMSE of time delay with the different K

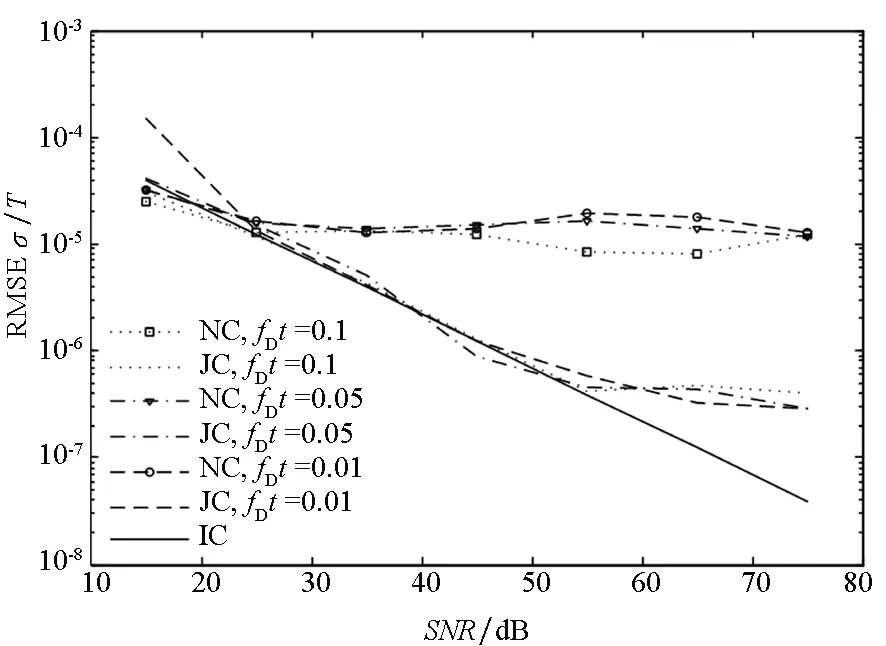
图4 不同fDT条件下时间参数估计的RMSEFig.4 RMSE of time delay with the different fDT

图5 不同相关带宽条件下时间参数估计的RMSEFig.5 RMSE of time delay with the different channel coherence bandwidth

此外，由图2可知,相位噪声参数v越小，相位噪声的影响越小，此时算法的时间测量精度越高。由图3可知,不采用补偿算法时，K值的越小，时间测量的精度越低，因为K值越小信道中非视距分量的功率越大，信道的衰落越严重。由图3、图4可知，在不同的Rician因子、不同的多普勒扩展的情况下，迭代算法皆可正常工作，显著提高系统的性能，且不同参数条件下算法的性能相似。由图5可知，信道的相关带宽越大，时间测量精度越高，因为相关带宽越大，信道的频率选择性越弱，信道特性越好。

4 结论

本文提出了一种衰落信道下时间延时参数、信道衰落参数、相位噪声参数联合估计的迭代算法。该算法不影响基于OFCDM的精确时间同步测量系统的最大不模糊时间，提高了系统在衰落信道以及大相噪条件下的测量精度。仿真结果表明，该算法可实现衰落参数与相噪参数的估计，实现精确时间测量时对信道衰落与相位噪声的补偿，提高了时间测量的RMSE性能。

References)

[1] Zhou Y Q, Wang J Z, Sawahashi M. Downlink transmission of broadband OFCDM systems—part I: hybrid detection[J]. IEEE Transaction on Communication, 2005, 53(4): 718-729.

[2] Miridakis N I, Vergados D D, Papadakis E. A receiver-centric OFCDM approach with subcarrier grouping[J].IEEE Communications Letters, 2012, 16(6): 761-764.

[3] Maeda N, Atarashi H, Sawahashi M. Performance comparison of channel interleaving methods in frequency domain for VSF-OFCDM broadband wireless access in forward link[J]. IEICE Transactions on Communications, 2003, 86(1): 300-313.

[4] Zhou Y Q, Wang J, Sawahashi M. OFCDM: a promising broadband wireless access technique[J]. IEEE Communications Magazine, 2008, 46(3): 38-49.

[5] Hussain F, Anpalagan A, Kong H Y. Performance analysis of two dimensional spreading for OFCDM femtocell users overlaid with OFDM macrocell[J]. Wireless Personal Communications, 2013, 72(1): 137-158.

[6] Gao K, Zhou Z W, Zou J B, et al. OFCDM-based precise time measurement and its performance under Gaussian channel[C]//Proceedings of International Conference on signal Processing and Communication Systems, 2013.

[7] Zou Q Y, Tarighat A, Sayed A H. Compensation of phase noise in OFDM wireless systems[J]. IEEE Transaction on Signal Processing, 2007, 55(11): 5407-5424.

[8] Zhang S, Zhang X L. A novel scheme of joint channel and phase noise compensation for Chinese DTMB system[J]. IEEE Transaction on Broadcasting, 2011, 57(1): 129-134.[9] Lin D D, Pacheco R A, Lim T J, et al. Joint estimation of channel response, frequency offset, and phase noise in OFDM[J]. IEEE Transaction on Signal Processing, 2006, 54(9): 3542-3554.

[10] 沈永欢. 实用数学手册[M]. 北京: 科学出版社, 1992. SHEN Yonghuan. Practical mathematics handbook[M]. Beijing: Science press, 1992. (in Chinese)

[11] Zhang G， Zhu Z D， Lu B. Algorithm for ambiguity resolution in range and velocity[J]. Transactions of Nanjing University of Aeronautics & Astronautics， 2001, 18(2): 219-223.

[12] Mccormick W S, Miller D E, Tsui J B Y.Resolution of a ambiguity problem in multiple frequency spectral estimation[J]. IEEE Transactions on Aerospace and Electronic Systems， 1995, 31(1): 2-8.

[13] Lee W C Y. Mobile communications engineering: theory and applications[M]. 2nd ed. USA: McGraw-Hill, 1997.

[14] Piazzo L, Mandarini P. Analysis of phase noise effects in OFDM modems[J]. IEEE Transaction on Communication, 2002, 50(10): 1696-1705.

[15] 高凯. MIMO信道的建模与仿真以及无线衰落信道的Markov模型研究[D]. 长沙： 国防科学技术大学， 2006. GAO Kai. Studies on modeling and simulation of MIMO channel and Markov model of wireless fading channel[D]. Changsha: National University of Defense Technology, 2006.(in Chinese)

Precise time measurement based on orthogonal frequency and code division multiplexing in fading channel

GAO Kai, ZHU Jiang, ZOU Jianbin, ZHANG Wei, ZHOU Ziwei

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

A novel communication system based on orthogonal frequency and code division multiplexing was proposed for precise time measurement in the fading channel, and a novel iterative algorithm was proposed to improve the performance caused by the fading channel and phase noise without reducing the maximum unambiguous time. In the scheme, the coefficients of fading channel and the phase noise were jointly estimated with the time delay. It is shown both by theory and computer simulations that the proposed scheme can effectively mitigate the time estimation error caused by fading channel and phase noise.

orthogonal frequency and code division multiplexing; diversity; spread spectrum; time measurement

10.11887/j.cn.201606024

2015-05-06

国家自然科学基金资助项目(61201166)

高凯(1978—)，男，江苏连云港人，副教授，博士，E-mail：gaokai000@nudt.edu.cn

TN953

A

1001-2486(2016)06-148-06

http://journal.nudt.edu.cn