含空位缺陷单壁碳纳米管断裂行为的有限元模拟

张 续， 齐乐华， 舒 扬， 付前刚， 李贺军

(1.西北工业大学 机电学院,陕西 西安710072；2.西北工业大学 材料学院,陕西 西安710072)

含空位缺陷单壁碳纳米管断裂行为的有限元模拟

张 续1， 齐乐华1， 舒 扬1， 付前刚2， 李贺军2

(1.西北工业大学 机电学院,陕西 西安710072；2.西北工业大学 材料学院,陕西 西安710072)

提出了碳碳键的断裂准则，建立了含空位缺陷碳纳米管的有限元模型，基于此断裂准则采用有限元方法对单壁碳纳米管的断裂行为进行了模拟研究，计算得到了碳纳米管的抗拉强度和极限应变，并研究了单原子空位缺陷对碳纳米管抗拉强度和极限应变的影响。结果表明理想单壁碳纳米管的抗拉强度约为100 GPa，极限应变约为20%。单原子空位缺陷显著降低了碳纳米管的抗拉强度和极限应变，使抗拉强度降低了20%～30%，极限应变降低了12%～18%，这也正是碳纳米管极限强度的实验结果远低于理论预测结果的原因。

单壁碳纳米管； 空位缺陷； 有限元法； 抗拉强度； 极限应变

1 前言

碳纳米管作为备受研究人员关注的纳米材料，具有优异的力学性能，在诸多领域应用潜力巨大。基于密度泛函理论(DFT)[1-3]、分子动力学方法(MD)[2, 4]以及分子力学方法(MM)[5,6]理论计算表明，碳纳米管的抗拉强度为85～220 GPa，显著高于Yu等[7]的实验结果(11～63 GPa)，这可能是由于实际制备的碳纳米管中存在的缺陷所造成的[5]。

目前，实验手段尚不能观测到碳纳米管的断裂过程，因此采用数值模的方法对碳纳米管断裂行为进行研究是一种有效的手段[8]。采用量子力学方法[3]、分子动力学方法[4]以及分子力学方法[5]对含缺陷碳纳米管研究表明：空位缺陷使得碳纳米管的抗拉强度下降20%～40%，极限应变下降10%～50%。然而上述方法都未对碳碳键的断裂进行定量描述。本文采用Morse势函数描述碳碳键的拉伸作用，通过分析其力-位移曲线的特性，提出了描述碳碳键断裂的数学公式，建立了含空位缺陷单壁碳纳米管的有限元模型，采用有限元方法对碳纳米管的断裂行为进行了模拟研究，为深入研究碳纳米管的断裂性质奠定了基础。

2 建模方法及分析

2.1 碳纳米管数学模型

碳纳米管分子结构的基本构成单元为碳原子形成的六边形网格结构(图1)。

图 1 碳纳米管结构的有限元模型Fig. 1 FEM model of a SWCNT.

将碳碳键看做是承载梁单元，碳原子看做是梁单元的节点，由此可以采用梁单元建立整个碳纳米管结构。其中梁单元的长度等于碳碳键长度ac-c(ac-c=0.142 nm[8])，梁单元的直径d等于碳碳键直径d0。以下是梁单元各项材料参数的确定。

由分子力学方法的原理知，化学键伸缩能Ur、化学键弯曲能Uθ、围绕单键的扭转能Uτ可以采用简单的谐和势函数表示[9]：

(1)

(2)

(3)

式中,kr、kθ和kτ分别表示化学键拉伸常数、化学键弯曲常数和化学键扭转常数[9]，Δr、Δθ和Δφ分别表示化学键拉伸增量、键角转动增量和键扭转增量。

由经典结构力学理论，长度为L的均匀梁在纯轴向拉力N、纯弯矩M、纯扭矩T作用下的应变能分别表示为：

(4)

(5)

(6)

式中,E、G分别为梁单元弹性模量和剪切模量；I、J分别为截面惯性矩和截面极惯性矩；ΔL、Δα、Δβ分别表示梁轴向拉伸变形量、梁端点的转角、梁端点的扭转角；A为横截面积。

由式(1)～式(6)可以得到如下的表达式：

(7)

由式(7)可以得到以下关系式：

(8)

将kr、kθ和kτ的值[8]带入式(8)便可以得到梁单元的各项参数：d=0.1466 nm，E=5.12 TPa，G=0.87 TPa。

2.2 碳碳键断裂准则

碳纳米管的断裂本质上是碳碳键的断裂[5]，因此研究碳纳米管的断裂行为，关键在于描述碳碳键的断裂机制。由Morse势函数[10]表达的化学键拉伸作用如下：

(9)

式中De、β为碳碳键的常数[11]，De=6.030 1510-19N·m，β=2.6251010m-1，r0=0.142 nm为变形前碳碳键键长，r为变形后碳碳键键长。将式(9)中碳碳键位移(r-r0)记作Δr，等式两边同时对Δr微分得碳碳键力-位移关系表达式：

(10)

由式(10)得到的碳碳键拉伸作用下力-位移曲线如图2所示。可以发现碳碳键的拉伸曲线表现出脆性材料的特性，即只有弹性阶段和断裂阶段：在力F达到最大值A点之前，力与位移成正比例关系，对应弹性阶段；在A点之后，力随位移增大迅速减小，而后逐渐消失，对应断裂阶段。对比脆性材料的特性，文中假设碳碳键在A点发生断裂失效，并将模拟加载过程中对梁单元的断裂准则定义为：一旦梁单元内某一点处的最大伸长线应变ε1达到简单拉伸时的破坏伸长应变εu时，梁单元便发生断裂失效，用公式表示为：

ε1=εu

(11)

图2中A点对应碳碳键应变为18.3%，故式中梁单元的破坏伸长应变εu=18.3%。

图 2 碳碳键拉伸作用下力-位移曲线Fig. 2 Force-displacement curve of C—C bond under axial force.

2.3 碳纳米管有限元分析中空位缺陷的实现

原子空位缺陷是碳纳米管中最常见的一种缺陷，是由于晶格原子的缺失形成的[12]。碳纳米管在制备、纯化或其他实验过程中都可能会引入空位缺陷[13,14]。文中仅考虑单原子空位缺陷对碳纳米管性质的影响。空位缺陷的处理方式为：在模拟加载前，将与缺失碳原子相连的三个碳碳键的刚度矩阵乘以一个很小的因子(默认为10-6)，因而其单元载荷可视为0，从而不对整个碳纳米管结构的载荷向量生效。图3是本文建立的含单原子空位缺陷单壁碳纳米管模型。模拟时，将碳纳米管一端原子固定，另一端原子施加轴向载荷。

图 3 含单原子空位缺陷碳纳米管模型 (a) (20, 0)锯齿型单壁碳纳米管; (b) (12, 12)扶手椅型单壁碳纳米管Fig. 3 Models of SWCNTs with single atom vacancy: (a) (20, 0)Zigzag SWCNT and (b) (12, 12)Armchair SWCNT.

3 计算结果与分析

在模拟加载过程中，将碳纳米管完全断裂之时的应力和应变分别称为碳纳米管的抗拉强度(σb)和极限应变(εb)，即：

(12)

式中,F为碳纳米管轴向力，dc为碳纳米管直径，h为碳纳米管厚度(此处取0.34 nm[15])，L0为碳纳米管变形前长度，Ld为碳纳米管变形后长度。表1为本文采用有限元方法与其他方法模拟结果的对比。从表1的数据中可以看出，本文采用的有限元方法得到的数据和文献[3,6,11]中各种方法模拟得到的数据误差在0.9%～18%之间，其差异是由于不同模拟方法所采用的数学模型不同而造成的。

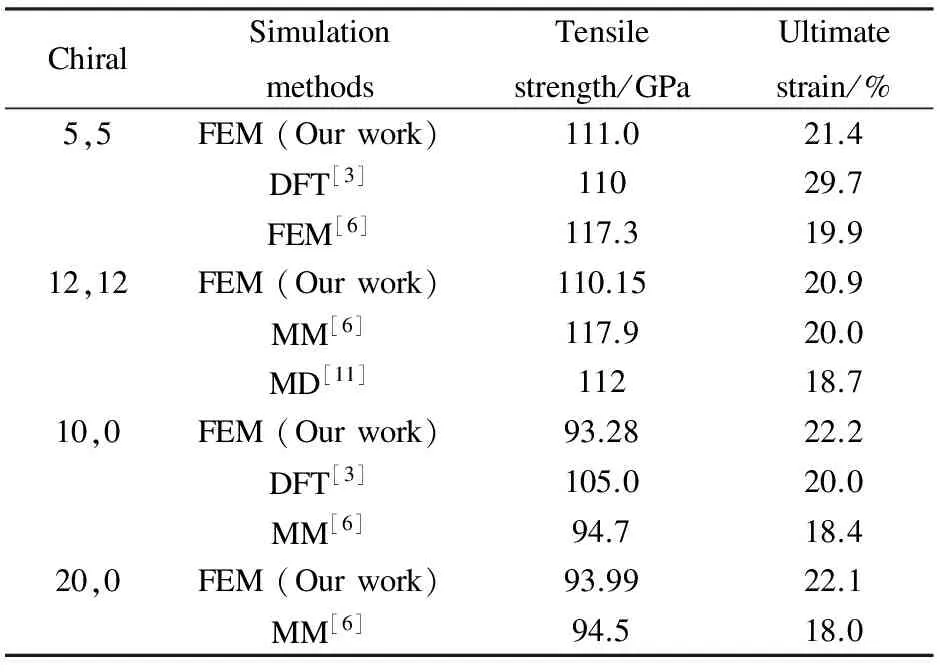
表 1 本文有限元方法与其它方法模拟结果对比Table 1 The simulation results by FEM and other simulation methods.

表2为采用本文方法计算的锯齿型和扶手椅型单壁碳纳米管的抗拉强度和极限应变。从表2可以看出：理想锯齿型碳纳米管抗拉强度在93 GPa左右、极限应变在22%左右；理想扶手椅型碳纳米管抗拉强度在110 GPa左右、极限应变在21%左右。单原子空位缺陷使锯齿型碳纳米管的抗拉强度和极限应变分别下降了30%和18%；使扶手椅型单壁碳纳米管的抗拉强度和极限应变分别下降了20%和12%。由此表明：在相同尺寸下，扶手椅型碳纳米管的抗拉强度略大于锯齿型碳纳米管的抗拉强度；单原子空位缺陷对锯齿型碳纳米管的抗拉强度和极限应影响更大。由于石墨烯在小变形下表现出各向同性性质，而在大变形下则表现出各向异性性质。单壁碳纳米管可以看做是由石墨烯卷曲而成，在大变形情况下其强度呈现各向异性性质，因此，缺陷对不同手性碳纳米管强度的影响程度有所差异[5]。

从图4可以看出：在应变大于10%以后，随着碳纳米管中应变的增大，手性对碳纳米管中应力的影响也逐渐变大。另外，对比图4中同一碳纳米管在含空位缺陷和不含缺陷时的应力-应变曲线可以看出，单原子空位缺陷极大地降低了碳纳米管的抗拉强度和极限应变，对其弹性模量影响甚小，这与文献[5]得出的结论相一致。

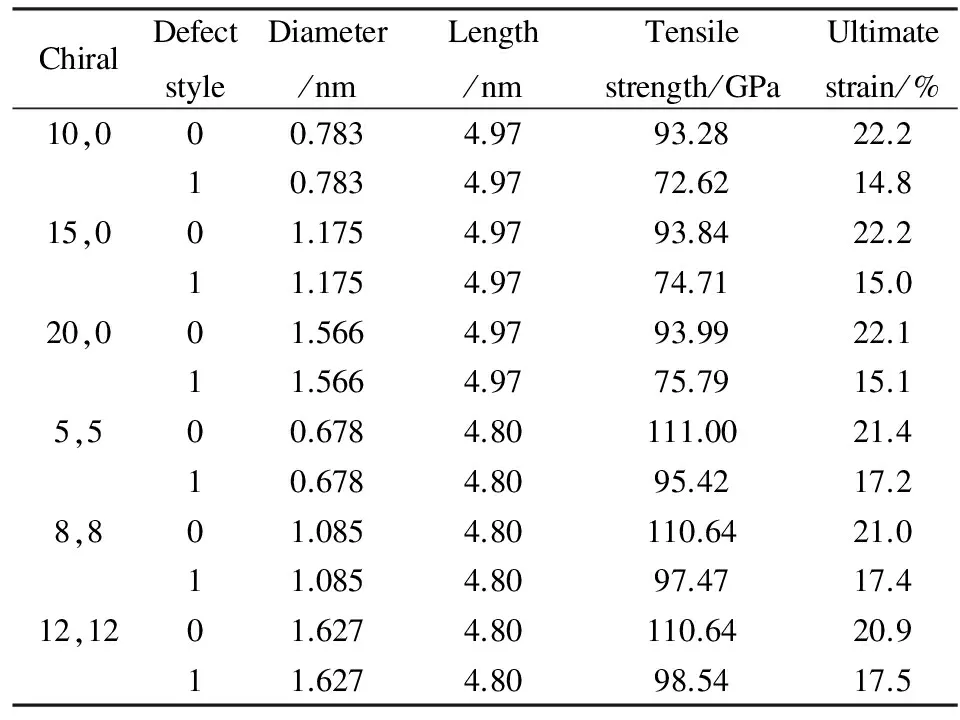
表 2 单壁碳纳米管抗拉强度和极限应变Tabel 2 Tensile strength and ultimate strain of SWCNTs.

Note： Defect style： 0: Perfect； 1: Single atomic vacancy.

图 4 单壁碳纳米管应力-应变曲线Fig. 4 Stress-strain curves of SWCNTs.

4 结论

理想单壁碳纳米管抗拉强度在100 GPa左右，极限应变在20%左右；单原子空位缺陷使单壁碳纳米管的抗拉强度下降了20%～30%、极限应变下降了12%～18%。空位缺陷对碳纳米管抗拉强度和极限应变影响较大，对弹性模量影响较小。随着碳纳米管中应变的增大，手性对碳纳米管抗拉强度和极限应变的影响变大。

[1] Ogata S, Shibutani Y. Ideal tensile strength and band gap of single-walled carbon nanotubes[J]. Phys Rev B, 2003, 68(16): 165409.

[2] Zhao Q Z, Nardelli M B, Bernholc J. Ultimate strength of carbon nanotubes: A theoretical study[J]. PHYSICAL REVIEW B, 2002, 65: 144105.

[3] Mielke S L, Troya D, Zhang S L, et al. The role of vacancy defects and holes in the fracture of carbon nanotubes[J]. Chemical Physics Letter, 2003, 382: 413-420.

[4] Talukdar K, Agrawala R, Mitra A K. Dependence of mechanical characteristics and the fracture and buckling behavior of single-walled carbon nanotubes on their geometry[J]. New Carbon Materials, 2011, 26(6): 408-416.

[5] Zu M, Li Q W, Zhu Y T, et al. The effective interfacial shear strength of carbon nanotube fibers in an epoxy matrix characterized by a microdroplet test[J]. Carbon, 2012, 50: 1271-1279.

[6] Meo M, Rossi M. A molecular-mechanics based finite element model for strength prediction of single wall carbon nanotubes[J]. Materials Science and Engineering A, 2007, 454-455: 170-177.

[7] Yu M F, Lourie O, Dyer M J, et al. Strength and breaking mechanism of multi-walled carbon nanotubes under tensile Load[J]. Science, 2000, 287: 637-640.

[8] 孙振锋, 齐乐华, 舒 扬, 等. 有限元方法的小管径单壁碳纳米管杨氏模量预测[J]. 西安交通大学学报, 2007, 41(9): 1066-1069. (SUN Zheng-feng, QI Le-hua, SHU Yang, et al. Prediction of young’s modulus of small diameter single-wall carbon nanotube with finite element method[J]. Lournal of Xi’an Jiao Tong University, 2007, 41(9): 1066-1069.)

[9] Li C Y, Chou T W. A structural mechanics approach for the analysis of carbon nanotubes[J]. International Journal of Solids and Structures, 2003, 40: 2487-2499.

[10] Girifalco L A, Weizer V G. Application of the Morse Potential Function to Cubic Metals[J]. Physical Review, 1959, 114 (3): 687-690.

[11] Belytschko T, Xiao S P, Schatz G C, et al. Atomistic simulations of nanotube fracture[J]. Physical Review B, 2002, 65: 235430.

[12] Lu A G, Pan B C. Nature of single vacancy in achiral carbon nanotubes[J]. Physical Review B Letters, 2004, 92(10): 105504.

[13] Paul S, Samdarshi S K. A green precursor for carbon nanotube synthesis[J]. New Carbon Materials, 2011, 26(2): 85-88.

[14] Dutta D, Dubey R, Yadav J, et al. Preparation of spongy microspheres consisting of functionalized multiwalled carbon nanotubes[J]. New Carbon Materials, 201126(2): 98-102.

[15] Arash B, Ansari R. Evaluation of nonlocal parameter in the vibrations of single-walled carbon nanotubes with initial strain[J]. Physica E, 2010, 42: 2058-2064.

Simulation of the fracture behavior of single-walled carbon nanotubes with a single atom vacancy by the finite element method

ZHANG Xu1, QI Le-hua1, SHU Yang1, FU Qian-gang2, LI He-jun2

(1.SchoolofMechanicalandElectricalEngineering,NorthwesternPolytechnicalUniversity,Xi’an710072,China;2.SchoolofMaterialsScienceandEngineering,NorthwesternPolytechnicalUniversity,Xi’an710072,China)

A finite element model of single-walled carbon nanotubes (SWCNTs) was established using ANSYS parametric design language, by which their fracture behavior was simulated on the platform of ANSYS using the criterion of the fracture of a carbon-carbon bond based on the Morse potential. The influence of a single atomic vacancy on the tensile strength and ultimate strain of SWCNTs was investigated. Results showed that the tensile strength and ultimate strain of perfect SWCNTs are about 120 GPa and 22%, respectively. Values for SWCNTs with the single vacancy are 20-30% and 12-18% less than those of the perfect ones. This is why the experimental tensile strengths of SWCNTs are far less than the theoretical predicted values. In addition, the tensile strengths of SWCNTs are anisotropic at large deformations, which agrees well with the simulation results obtained using molecular mechanics.

Single-walled carbon nanotubes; Finite element method; Vacancy; Tensile strength; Ultimate strain.

QI Le-hua, Ph. D, Professor. E-mail: qilehua@nwpu.edu.cn.

1007-8827(2016)06-0646-05

TB332

A

2016-07-20；

2016-12-06

国家自然科学基金(51275417,51221001).

齐乐华，博士，教授.E-mail： qilehua@nwpu.end.cn

张 续，硕士研究生.E-mail： zhangxu7513@163.com

FoundationItems: National Natural Science Foundation of China (51275417, 51221001).

Authorintroduction: ZHANG Xu, Master Student. E-mail: zhangxu7513@163.com.