不同信道环境的激光水下传输仿真

胡 鑫，张祥金

(南京理工大学 机械工程学院，南京 210094)

【光学工程与电子技术】

不同信道环境的激光水下传输仿真

胡 鑫，张祥金

(南京理工大学 机械工程学院，南京 210094)

为更深入研究水下激光在武器探测及通信中的应用与不同信道环境传输过程中的特性，验证蒙特卡洛法仿真在水下激光传输中，关于水下散射体直径、密度和距离对接收光子权重、单光子散射次数以及时间展宽的影响，将米氏散射解析模型与蒙特卡罗法仿真结合，通过改变米氏散射模型中的散射体直径、密度以及传输距离从而改变仿真过程中需设置的散射系数、消光系数、不对称因子以及光子自由运动距离，得到其仿真结果关于光子权重随散射体直径、密度以及传输距离的增大而减小的结论，分析了造成其结果的原因；研究了水下散射体直径在蒙特卡洛罗仿真中对单光子平均散射次数的影响。仿真结果表明：在米氏散射模型中单光子散射次数随着散射体直径的增大而增加，分析了散射体直径对造成时间展宽的影响。

米氏散射模型；蒙特卡洛法；散射体直径；散射体密度；传输距离

1963年S.A.Sullivan和S.Q.Duntely等人发现在海水中也存在一个类似于大气的透光窗口[1]，海水对 470～580 nm 波长的蓝绿光衰减性较小。由于激光高频率、方向性好、传送信息量大，且不受干扰，在水下通信中能有效解决通信距离、速率以及安全方面的矛盾，成为近年来水下无线通信领域关注和研究的热点之一[2]。美国、欧洲、日本等国家均投入了大量的财力和技术力量于激光通信领域[3]。目前蓝绿激光水下通信及探测主要运用于水下鱼雷信息装定以及对潜通信方面，包括下行激光，即机载或卫星携带激光雷达对潜艇的探测和上行激光的传输[4-6]。尽管水下激光通信有很好的发展前景，但同样也存在技术难点，包括海水信道的复杂性对激光传输的影响；高精度、高概率、高速的光束对准；大容量、远距离的技术要求等[7]。增大信息传递量及减小时域展宽、误码率，对信道模型的建立以及研究不同信道条件下激光的传输特性对于解决以上难点有着重要作用[8]。

目前对激光传输的模拟方法有小角度近似法、唯像方程法和蒙特卡洛法。小角度近似法是将光在水中的散射角度看作很小的前向散射角，即将散射能量集中在偏离传播方向附近很小的角度内进行计算[9]，但不能反映光子传输过程中散射的多样性以及信道的复杂性。美国的Mooradian等[10]获得了理想某时域激光脉冲在水中传输时的波形表达形式，即唯像方程，获得了不同水质以及距离下的时域波形。该方法也是在较理想的情况下得到的模拟波形方程，只能得到特定水质及有限距离下的数据参数[11]。很多文章多用蒙特卡洛法模拟仿真光子传输，但基本都是在特定的散射系数、不对称因子等参数一定的条件下进行的，本研究结合了米氏散射解析法以及蒙特卡洛法对光子的传输及信道的条件进行模拟仿真。

1 米氏散射

将水下的光学散射可大致分为分子的瑞利散射以及大分子、颗粒以及悬浮物质的米氏散射。在纯水或杂质较少的水下环境里一般只考虑瑞利散射，而在含有各种杂质以及浮游动植物的海水里，应同时考虑瑞利散射和米氏散射。就水分子等尺寸相对于入射波长较小分子而言，发生瑞利散射时，其沿散射方向的辐射强度与波长的四次方成反比并且各向同性。同时由于瑞丽散射受海水压强、温度、粒子尺寸及密度等因素影响不大，并且经美国海军航空系统司令部(NAVAIR)在2009年研究中心进行的激光通信水槽实验，证实了激光水下传输前向散射光强远大于后向散射光强，还是10倍及以上的准直光强[12]。因此将海水中的散射模型简化为米氏散射。其中散射系数ksca和消光系数kext的有效因子Ksca、Kext分别为：

(1)

(2)

an和bn为米氏散射的两个重要系数，

(3)

(4)

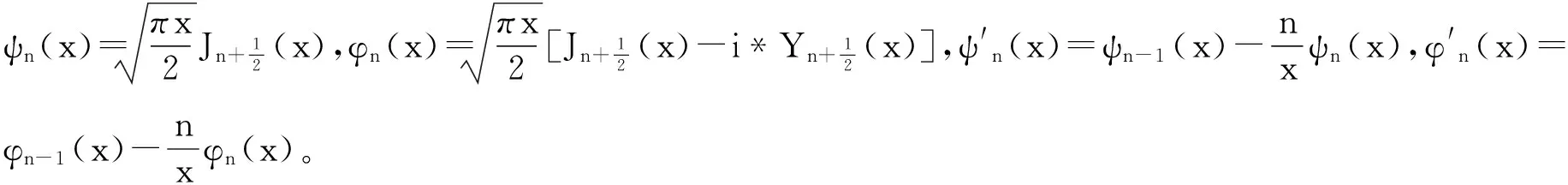
由以上的解析式利用Matlab对Ksca、Kext进行计算仿真，由米氏理论可知，当入射光波长与散射体尺寸相当时，发生米氏散射。由图1曲线可知，当粒子直径与入射光波长关系在符合米氏散射要求范围以内时，散射有效因子和消光有效因子取值均逐渐趋于稳定；当粒子直径过小时，米氏散射很少并随直径尺寸增加而增加；当粒子直径尺寸过大时，将会发生含有镜面反射、漫反射等多种散射类型并且后向散射增大。

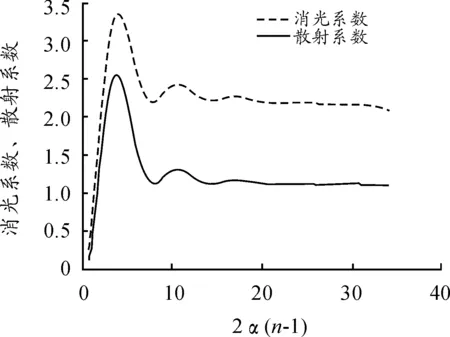
λ=450 nm, m=1.34-0.05i， a=10-6 m

散射系数和消光系数为：

ksca=KscaNπa2/4

(5)

kext=KextNπa2/4

(6)

其中N为单位体积海水中散射粒子的个数。

2 HG散射相函数

在米氏散射模型中，最常用的散射相函数是Henyey-Greenstein 散射相函数，以下简称HG相函数，其表达式为

(7)

式中：θ是散射角；g是不对称因子。

不对称因子g的表达式为

(8)

通过解析式利用Matlab对不对称因子g的值进行仿真，如图2所示，当在米氏散射范围内，不对称因子取值基本在0.9～1。并且其受相对折射率等光学常数的变化影响较小[14]，因此，粒子的直径是影响不对称因子的主要因素。由于不对称因子g的计算公式是根据米氏散射理论得到，当粒子尺寸与入射光波长关系不满足米氏散射时，不对乘系数取值变化不规则，如图2所示，曲线后半段的不对称因子变化不再满足稳定规律，因尺寸参数α=π*a/λ大于50，粒子直径远大于波长。

λ=450 nm, m=1.34-0.05i， a=10-6 m

3 蒙特卡洛法仿真

蒙特卡罗仿真方法在光子运动轨迹仿真方面运用非常广泛，它根据光子以及信道模型确定光子在传输过程中的运动轨迹，设置光子的初始位置、运动距离以及权重。初始位置为(0,0,0)，初始方向(0,0,1)，初始权重wc=1。对光子的自由运动路程l进行随机取值

(9)

即光子自由运动l后与散射体碰撞，其中β为[0,1]之间的随机数。当光子进行一次碰撞并发生散射，其权重衰减至wc=Ksca/Kext，当权重衰减至0.000 1及以下或者光子超出接收范围则将其视为消亡状态。它的运动流程如图3所示。

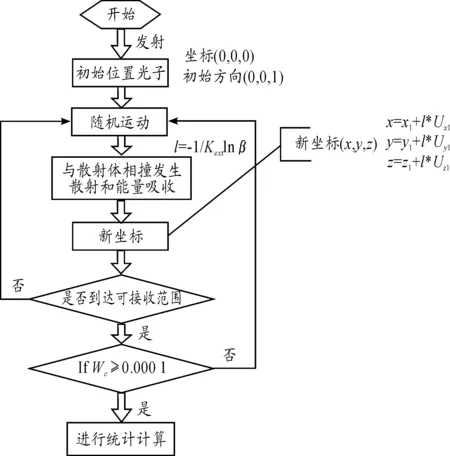
图3 蒙特卡罗法仿真流程

由图3的流程可知，当光子经过一段随机运动并发生散射时，新的坐标位置

x=x1+Ux1*l

y=y1+Uy1*l

z=z1+Uz1*l

(10)

当Uz≥0.999时

Ux1=sinθ*cosφ

Uy1=sinθsinφ

Uz1=|Uz1|/Uz1*cosθ

(11)

否则按式(12)计算

(12)

式中：(x1，y1，z1)是光子上次碰撞位置；(Ux，Uy，Uz)是光子入射方向；θ为散射角，根据HG散射相函数

(13)

式中：φ是散射俯仰角，φ=2πζ，ζ为[0,1]的随机数[15]。

将蒙特卡罗法与上述米氏散射的解析式相结合，结合上式(5)、式(6)、式(8)通过在米氏散射模型下，改变解析式中粒子直径、密度、传输距离等变量改变散射系数、消光系数、不对称因子以及光子自由运动路程，将得到的散射系数、消光系数不对称因子和光子自由运动路程等参数作为变量，利用蒙特卡洛法来对光子传输过程和结果仿真，得到不同粒子直径、密度、传输距离下光子的权重以及散射次数的关系。

在蒙特卡洛模拟中，随着传输距离、粒子密度的增加，单光子在路径上的散射次数增加，并且权重减小。而粒子直径对单光子的散射次数以及到达接收面权重的影响如图4所示。图4(a)反映了随着水中悬浮粒子直径的增加，到达接收面的权重减少。这是由于光子在水下经历多次散射，并且散射次数增加，特别是当粒子直径增大时，后向散射更见明显。粒子直径尺寸越大，经蒙特卡洛仿真后到达接收面的光子权重越少，时间展宽越小。在仿真过程中，为使结果更直观，将到达接收面权重增大6 250倍，因此实际上到达接收面的权重将会更少。而图4(b)反映了随着粒子直径的增加，单个光子在路径中的平均散射次数也逐渐增加。综合图4(a)、图4(b)，散射粒子直径增加，散射次数增加，到达接收面的权重减小，而时间展宽没有随散射次数的增加而增加是因为单光子散射次数较多使得权重衰减大、光子偏离严重，因而到达接收面的能量大大减小，测得时间展宽所需的光子能量已在传输过程中大量衰减并且偏移，因此已经不足以有足够的能量造成时间展宽。

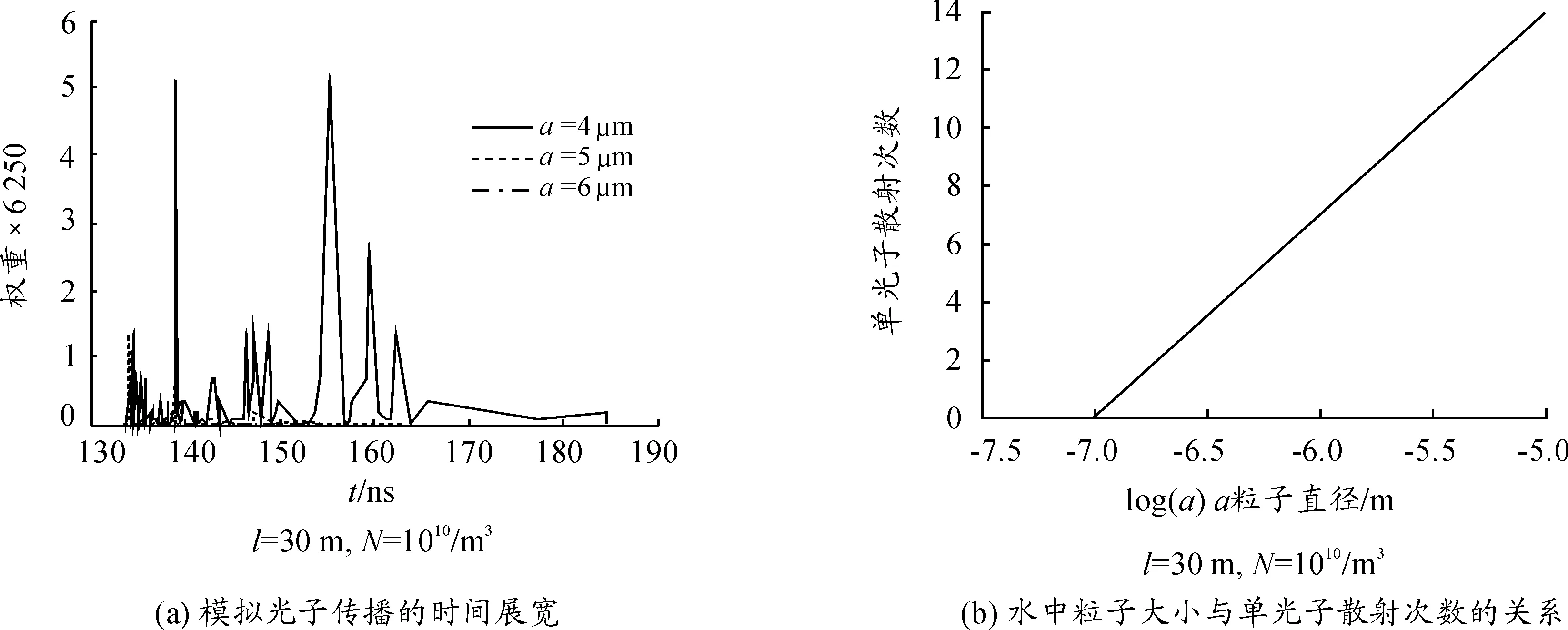
图4 粒子直径对单光子的散射次数以及到达接收面权重的影响

图5 不同水下环境中光子到达接收面权重

4 结论

本文将米氏散射模型解析与蒙塔卡罗仿真结合，根据散射体直径、散射体密度等影响因子对散射系数、消光系数，不对称因子以及光子自由运动路程等蒙特卡洛仿真中所需变量的影响，经仿真结果得到了光子到达接收面的权重随着散射体直径、散射体密度以及传输距离的增加而减少的结论，在散射体密度≥1013/m3时，接收距离≥3 m处，到达接收面的光子权重已经接近0；仿真结果同样表明，由于粒子直径增大造成单光子的更多次散射，特别是后向散射，使得接收面光子权重大大减少，同时，距离增大和散射体密度增加同样也造成了多次散射并引起的能量大量衰减以及传输位置轴向偏移严重，使得到达接收面权重骤减，并且已经不足以满足时间展宽所需光子能量。

将仿真结果与已有的ICCD(Intensified CCD)光波门宽度检测激光脉冲峰值能量的实验结果以及小角度近似法和唯像方程法仿真结果[11,16]对比表明：光在水下传输时，辐射能随着传输距离的增加而减少，并且散射次数增大也会使接收到的辐射能减少，与仿真结果符合。与衰减系数和水体浊度关系的实验[17]进行比较时发现，水中散射体密度增加导致消光系数增大，从而使接受辐射能减小，与仿真结果基本吻合；但在散射体粒径较大时(≥10 μm)，结果并不与仿真结果一致，这是因为本文设置的粒径都是在1～10 μm满足米氏散射条件，并没有对含粒径大于10 μm的散射体信道进行仿真。

本文的研究将为激光在水下通信时信道模型的建立以及对减小通讯误码率等问题的进一步研究奠定了一定的基础。

[1] DUNTLEY Q.Light in the sea[J].J Opt Soc Am B,1963,53:214-223.

[2] 邹家轩，敖发良.PPM水下激光通信同步技术的研究[J].微计算机信息，2010,26(2)：159-160.

[3] 付强，姜会林，王晓曼.空间激光通信研究现状及发展趋势[J].中国光学,2012,2(5):116-125.

[4] 李东杰，黄莎玲，彭波.水下激光成像技术研究进展及其在鱼雷引信系统的应用[J].声学技术，2014,33(4)：419-423.

[5] LIU Jintao，CHEN Weibiao.Uplink Laser Communications Between a Satellite and a Submerged Platform[J].Acta Photonica Sinica,2010,39(4):693-698.

[6] ZHOU Tianhua，CHEN Weibiao，HE Yan.Beam Spatial Distribution of Upward Laser Through Sea Air Linter-Face[J].Chinese Journal of Lasers，2010,37(8)：1978-1982.

[7] 周亚民，刘兵.激光对潜通信的发展及存在的问题[J].数字技术与应用，2014(8)：36-36.

[8] 沈娜，郭婧，张祥金.激光水下通讯误码率的影响[J].红外与激光工程，2012，41(11)：2935-2939.

[9] LINDA JEANNE MULLEN,AMARILDO J C.VIEIA PETER R.Herezfeld，Vineent Miehael Contarino.Application of RADAR Technology to Aerial LIDAR Systems for Enhancement of Shallow Underwater Target Detection[J].IEEE Transaction on Microwave Theory and Tecniques,1995,43(9):2370-2376.

[10]MOORADIAN G C，KERWERN G.Peiro Bruscaglioni.Simple Inexpensive Method of Measuring the Temparol Spreading of a Light Pulse Propagating in a Turbid Medium[J].Appl Opt.，1990,29(27)：3938-3944.

[11]章正宇，周寿桓，眭晓林.激光脉冲水中传输时域展宽特性的分析计算[J].光学学报，2003,23(7)：850-854.

[12]MULLEN L,LAUX A,COCHENOUR B.Propagation of Modulated Light in Water:Implications for Imaging and Communications Systems[J].Applied Optics,2009，48(14):2607-2612.

[13]尚廷义， 丁国超.Mie散射参量与球形粒子相对折射率规律的研究[J].牡丹江师范学院学报，2013(1)：14-16.

[14]陈明,田岩,彭复员,等.HG 散射相函数中非对称因子研究[J].中国科技大学学报，2009，37(9)：25-28.

[15]WANG Lihong,STEVEN L.JACQUES，ZHENG Liqiong.MCML—Monte Carlo Modeling of Light Transport in Multi-Layered Tissues[J].Computer Methods and Programs in Biomedicine，1995(47):131-146.

[16]李仅伟，毕卫红，任炎辉.水下激光通信中脉冲时域展宽的模拟计算方法[J].光学技术，2012，38(5)：569-572.

[17]丁琨，黄有为,金伟其.水下蓝绿激光传输的衰减系数与水体浊度关系的实验研究[J].红外技术，2013，25(8)：467-471.

(责任编辑杨继森)

Lasers’ Underwater Transmission Simulations in Various Channel Environments

HU Xin，ZHANG Xiang-jin

(School of Mechanical Engineering, Nanjing University of Science and Technology， Nanjing 210094, China)

In order to further study the underwater laser application in weapon scanning, communication and its characteristics in the various channel environments during the transmission processes, and to verify the influences of the underwater scatterers’ diameters, density and distance to received photon weight, single photon’s scattering number and time broadening with the Monte Carlo method, this thesis combined Mie scattering analytic model with Monte Carlo simulation, and it changed scattering coefficient, extinction coefficient, asymmetry factor and photon’s free play distance which should be set in the simulation process to change the Mie scattering analytic model’s scatterers’ diameters, density and transmission distance, resulting in the theory that the photon weight decreases when scatterers’ diameters, density and transmission distance increase, which is given by simulation report and the reasons of this phenomenon are also be represented with analysis; and we studied the influence of underwater scatterer’s diameter to the average scattering numbers of single photon in Monte Carlo simulation. The result shows that single photon’s scattering number will increase along with the increase of scatterers’ diameters and it also analyzes the influence of scatterer’s diameter to time broadening.

Mie scattering analytic model; Monte Carlo Method; scatterers’ diameter; scatterers’ density; transmission distance

2016-07-22；

武器装备预研基金项目(9140c300106150c30001)；中央高校基金本科研业务费专项资金资助(30915011334)

胡鑫(1991—)，女，硕士研究生，主要从事激光探测及装定研究。

张祥金,E-mail：zhangxiangjin@njust.edu.cn。

10.11809/scbgxb2016.12.032

胡鑫，张祥金.不同信道环境的激光水下传输仿真[J].兵器装备工程学报，2016(12):140-144.

format:HU Xin，ZHANG Xiang-jin.Lasers’ Underwater Transmission Simulations in Various Channel Environments[J].Journal of Ordnance Equipment Engineering,2016(12):140-144.

TJ430.6

A

2096-2304(2016)12-0140-05

修回日期：2016-08-15