预加应变对硫化橡胶损伤性能影响的试验研究
2017-01-06李晓雷李欣业桑建兵郄彦辉张铖博
李晓雷,李欣业,桑建兵,郄彦辉,张铖博
(河北工业大学 机械工程学院,天津 300130)
预加应变对硫化橡胶损伤性能影响的试验研究
李晓雷,李欣业,桑建兵,郄彦辉,张铖博
(河北工业大学 机械工程学院,天津 300130)
通过对一种硫化橡胶在单轴拉伸条件下进行的循环加载试验,得到了不同速率和不同预应变条件下材料的应力-应变关系曲线,由此分析了不同加载速率及预应变条件对硫化橡胶材料力学性能的影响.分别以应变能密度峰值、加载段所围面积和弹性模量法计算损伤参量,基于试验结果分析了硫化橡胶在不同预加应变条件下的损伤性能.研究结果表明:循环加载情况下,硫化橡胶的主应力峰值随加载速率的升高而增大,力学性能随循环次数的增加而趋于稳定;在预加应变条件下,硫化橡胶材料的损伤变化呈非线性增长,预应变量保持在0.3倍拉伸比以内能达到较好的使用效果.
硫化橡胶;大变形;损伤参量;实验分析;预应变
0 引言
橡胶材料因其具有独特的非线性力学行为,以及成本低廉、易于加工、优异的物理化学特性等一般工程材料难以比拟的优点,近年来在现代社会生活各个领域,特别是在航空航天等高科技领域的应用日益广泛,因此对橡胶材料力学特性的研究已成为重要的前沿性课题[1-3].橡胶器件在机构中是一类看似简单,其实非常复杂和重要的基础构件,对机构整体的工作性能、安全可靠性及环境保护功能都有非常重要的影响,一旦失效,往往会导致灾难性的后果.比如1986年美国挑战者号航天飞机推进器上的橡胶O型环失效导致火箭爆炸[4],1994年的“爱沙尼亚号”沉船惨案[5]和2012年韩国“罗老号”由于橡胶垫破损造成运载火箭的推迟发射,无不给社会带来重大安全和环境事故,造成重大的经济和生命损失.这些事故表明人们对橡胶材料损伤性能的研究与失效分析是亟待解决的问题.橡胶材料的材料特性和几何特性都是非线性的,其应力应变关系必须由超弹性理论[6-7]给出.而且橡胶材料的物理力学性质对外界因素的影响比较敏感,刘宇艳等[8]的研究结果表明,应力幅值和加载频率对橡胶材料性能有较大影响.上官文斌等[9-10]发现应变比对橡胶材料的损伤性能也有很大的影响.橡胶材料服役过程中长期处于低幅循环受力状态[11],使用前往往会施加或产生一定的预应变,例如轮胎、减震垫、传送带等橡胶制品.预应变会对橡胶材料的力学性能产生影响[12],进而影响实际橡胶制品的使用寿命.已有的工作研究的是橡胶材料在自然状态下的力学性能,施加预应变条件下橡胶材料力学性能的研究工作还不多,因此研究预应变对橡胶材料损伤性能的影响是十分必要的.
本文的目的是分析硫化橡胶材料在单向拉伸的循环加载条件下的大变形力学行为,讨论加载速率和预应变对橡胶材料的应力-应变关系和材料的损伤等力学性能的影响.利用Instron3365电子万能材料试验机,得到了一类硫化橡胶材料在不同加载速率和不同预应变条件下的应力-应变关系曲线,分析了硫化橡胶材料在循环加载条件下的加载速率和损伤特性.基于实验结果,利用3类损伤变量表征材料的损伤程度,并分析了预应变对材料损伤性能的影响.
1 试验
1.1 试验装置
本文循环加载试验在INSTRON 3365电子万能材料试验机上进行,最大载荷5 kN,其力值和位移精度均为0.5级,加载速率范围为0.0005~1000mm/m in.试验过程中如荷载比等于定值,试验机将自动终止试验.整个试验操作过程根据GB/T 258-2009[13]进行,外加载荷和试件变形由试验机自行测量并记录,最后通过应力-应变关系曲线表示出来.
1.2 试件
本文所制备试样的形状与尺寸满足国家标准《硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》(GB/T 258-2009)中“1型”哑铃状试样的要求,橡胶材料为通用硫化橡胶材料板,厚度为2mm,试验段长25mm,宽6mm.
1.3 测试方法
试验加载过程采用循环加载方式,加载速率和行程由位移控制,材料轴向变形选用25mm标距的大变形引伸仪记录.夹具选用适用于橡胶材料拉伸实验的自夹紧气动夹具,此夹具随着拉伸力的增大,夹具钳口对试样的夹持也越来越紧,避免了试样夹持部分的滑脱.循环加载速率和循环次数在INSTRON 3365电子万能材料试验机软件中根据要求设定.
1.4 试验结果及分析
1.4.1 不同加载速率下硫化橡胶材料的循环加载试验
橡胶材料在恒定拉伸比的往复拉伸变形过程中,从第2次循环开始的加载段曲线会远远低于首次循环的加载段曲线,当达到最大拉伸比时,卸载过程中的应力峰值也会远小于首次加载到最大主应变量时的应力值,从而会生成滞后环.其第1次循环时滞后环的面积最大,第2次循环时滞后环的面积小一些,之后依次递减,这种非线性应力软化反应即为Mullins效应.对于处于单向拉伸状态的不可压橡胶材料而言,其主应变为

其中:为试件在拉伸方向的主应变;L0和L分别为试件测量段的初始长度和最终长度.材料的主应力分别为

其中:F为所施加的载荷;A0为试件测量段的初始横截面面积.
在室温环境下分别以20mm/m in、50mm/m in、100mm/m in、200mm/m in、300mm/m in、400mm/min、500 mm/min的加载速率对橡胶材料进行单轴循环加载试验,使用1型哑铃型试件,加载最大应变为1倍拉伸比长度(即有效长度伸长25mm),预加载为0.2N,以消除试件在夹持过程中的变形.图1为不同加载速率下的应力-应变关系曲线,V为加载速率.

图1 不同速率下应力-应变关系曲线Fig.1 Stress-strain curvesatdifferentvelocities
等拉伸比条件下,不同加载速率时橡胶材料首循环主应力峰值随加载速率的变化曲线如图2所示,不同加载速率时应变能密度峰值与循环次数的关系曲线如图3所示.
从图2可见,在室温条件下,随着循环加载速率的增加,材料的首循环主应力峰值呈非线性增长,但增长趋势逐渐趋于平缓.图3表明,在拉伸比不变的情况下,当循环次数超过10次左右时,材料的应变能密度峰值将不再发生明显的变化.因此,硫化橡胶材料对加载速率和循环次数均非常敏感,其力学性能强烈地依赖于加载速率和循环次数,特别是加载速率和循环次数增长初期反应更为敏感.根据高分子材料的基本理论,由于硫化橡胶材料网状的高分子链结构的充分伸展需要时间,随加载速率的减小和循环次数的增加,硫化橡胶材料网状的高分子链结构能够得以充分的伸展,因而硫化橡胶材料的力学性能随着加载速率和循环次数的增大将趋于稳定.

图2 首循环主应力峰值与加载速率关系曲线Fig.2 Relationship between the principalstresspeaks at the first loop and loading rates
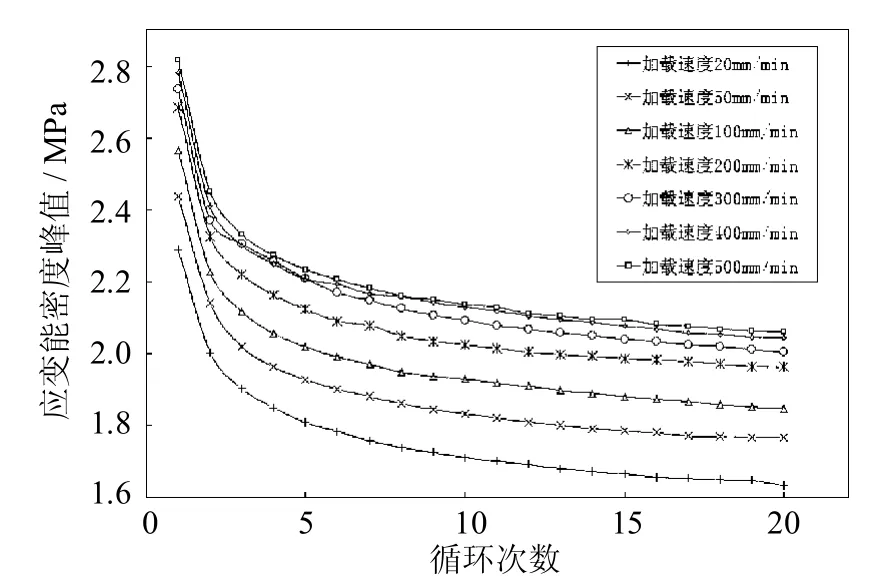
图3 应变能密度峰值与循环次数关系曲线Fig.3 Relationship between strain energy density peaksand cycle index
1.4.2 不同预应变时硫化橡胶材料的循环加载试验
将试件分别拉伸到0.1倍、0.2倍、0.3倍、0.4倍、0.5倍、0.6倍、0.7倍、0.8倍预应变.以0.1倍拉伸比为例,将引伸计标记的有效长度拉伸0.1倍拉伸比(即2.5mm),保持此状态在标准温度24℃下长时间放置使材料内部力学性能达到稳定状态,再以50 mm/m in的速率、1倍拉伸比(即25 mm)进行20次循环加载.图4为不同预应变单轴循环加载实验时的应力-应变关系曲线.
首先将不同预应变首循环的应力应变曲线进行对比,如图5所示.
图中可以看出,随着预应变量的增加,首循环最大主应力值也在增加,且在0.5倍预应变后增加幅度明显加大,第1次循环中加载与卸载过程中的应力曲线间的幅度也在不断增大,也即是应力软化现象更加明显.


图4 不同预应变时应力-应变关系曲线Fig.4 Stress-strain curvesatdifferentpre-strain deformations
2 硫化橡胶材料损伤性能研究
橡胶材料在服役过程中,受到外力作用和外界条件的影响时材料内部会产生微小的损坏,使得材料力学性能下降,这一变化过程称为损伤.不同于小变形的金属,对于橡胶这类大变形的材料,选作材料损伤参量的有应变能密度峰值、加载段所围面积和弹性模量法.下面对这些损伤参量的计算进行说明.
2.1 应变能密度峰值
应变能密度dw从能量的角度来对损伤量的变化进行表示,具体代表的是材料在变形过程中内部所产生的能量.通过下式,可以对应变能密度进行计算:


图5 不同预应变首循环曲线Fig.5 The first loopsatdifferentpre-strain
当材料仅到受单轴作用力时,在受力过程中所产生的应变能W为:

使得材料在一阶段内的能量损伤计算更为容易,马尔斯在比较应变能密度峰值与工程应变的变化规律时,利用的是加载段的实验参数作为依据,而迪森等在对橡胶材料试件进行同样分析后得出分析结果显示,采用卸载段实验参数作为依据,同样可以表示出材料在受力过程中内部能量损伤的变化规律.在实验研究中,选择变化幅度更大的加载段曲线参数进行计算.
分析以上的实验数据,图6给出了不同预应变时,在前20次循环过程中损伤量的变化规律.可以看到橡胶材料在0到0.1倍预应变之间,预应变量会对材料损伤产生较大的影响,之后0.1到0.3倍预应变间变化较为平缓,当预应变达到0.3倍预应变后损伤量会随预应变的增加产生较大变化,且当预应变量达到0.6倍预应变后,变化更为明显.综上所述,橡胶产品在实际使用过程中,当处于单向受力变化状态且需要加入预紧力的情况时,将预应变量保持在0.1到0.3倍预应变之内较为合理.

图6 应变能密度表征的损伤量与预应变关系曲线Fig.6 Relationship between damageof strain energy density and pre-strain
2.2 加载段所围面积法
材料循环加载曲线各周期变化规律会发现每下次的循环加载段曲线都会低于前1次循环加载段曲线,基于Mullins效应理论,相邻周期的加载段变化幅值可用来表示材料受力过程中的软化程度,也即是材料力学性能的变化程度.2次循环加载段曲线变化幅度(也就是两加载段曲线所围成面积)也可以用来表示损伤的变化量,同时这种损伤量计算方法包括了材料在整个受力状态下的力学性能变化规律,使其计算结果也就更为准确,进而形成利用多次循环加载段曲线所围成面积表示损伤量.有固定拉伸幅度的橡胶材料在循环载荷条件下的第1次循环中,加卸载路径主应力幅值最大.许多实验研究表明,在前两次循环期间的应力软化是最关键的,而循环过程中的加载曲线之间的面积大小也可用来表示2次循环之间损伤量的变化,或表示Mullins效应中应力软化的程度.为了使结果更加明显,这里取第10次循环曲线用来比较损伤量变化,图7所示为第1次循环与第10次循环的应力应变关系曲线.

图7 第1次和第10次循环应力应变关系曲线Fig7 Stress-strain curvesof the first loop and the tenth loop and pre-strain
设上方加载段曲线方程为

所取项数越多,结果越为准确,同时为方便计算在加载段数据点中取7点坐标(为更为准确得到拟合方程,在变化明显处选取点要密一些,如上图中的线型曲线则分别取0.1、0.2、0.3、0.4、0.6、0.9、1.1应变量值)代入,得到矩阵方程

可看作A B=C,将其代入MATLAB中进行计算,在定义A、C后利用

进行计算,得到B矩阵各数值

即方程:

拟合出上方加载段曲线拟合方程后,继续计算下方加载段曲线拟合方程,结果如下:

然后,利用下述方程计算得到所围面积

实验中2次循环间产生的损伤量可以用2次加载曲线加载段所围成的面积进行表示,图8为不同预应变时面积法计算损伤量的示意图.

图8 不同预应变的面积法计算示意图Fig.8 Sketch of enclosed areasatdifferentpre-strain
采用上面的方法,以0.1倍预应变实验参数为例进行计算,得目标方程f1x= 31.259 8 x6+112.207 7 x5160.576 6 x4+119.422 9 x350.970 4 x2+14.733 0 x 1.1225为0.1倍预应变实验首次循环加载段拟合方程,且x∈ (0.1,1.1).
得到第1次循环加载段拟合方程后,继续计算第10次循环加载段拟合方程,结果如下

计算后,得到不同预应变曲线所围面积结果如表1.

表1 不同预应变时面积法损伤量计算结果Tab.1 Enclosed areasof loading curvesatdifferentpre-strains
2.3 弹性模量法损伤量分析
弹性模量法,是以弹性模量计算出损伤参量并进行分析与比较损伤程度的计算方法,并从能量角度进行计算.材料的弹性模量可以表达材料在某一特定时刻的内部性能特性,此时利用材料在损伤过程中2时刻的弹性模量就可以对比出在这2个时刻之间材料内部的损伤量大小,其中表示损伤量变化程度的量(损伤度)可表示为

式中,E'、E分别代表的是材料受力前、后的弹性模量.根据材料弹性模量的混合法则

式中:V,Vc分别是总体积和微孔洞所占面积;Ec为微孔洞的弹性模量(=0).如定义=Vc/V,则损伤度为

式中,E'和E分别为无损伤和受损伤材料的杨氏模量.

表2 不同预应变时损伤度值表Tab.2 Damages atdifferentpre-strains
从式 (13)中可以看出,弹性模量法计算损伤量,所选取的为受力过程中2个瞬时变量,这就可以准确的计算变形过程中2个瞬时状态之间所产生的损伤量,与应变能密度峰值等损伤量相比,可计算的范围更大.
2.4 硫化橡胶材料损伤性能分析
用3种方法计算损伤量的结果如图9所示.由于多组损伤参数单位级数不同,将其进行无量纲化,得到图10.
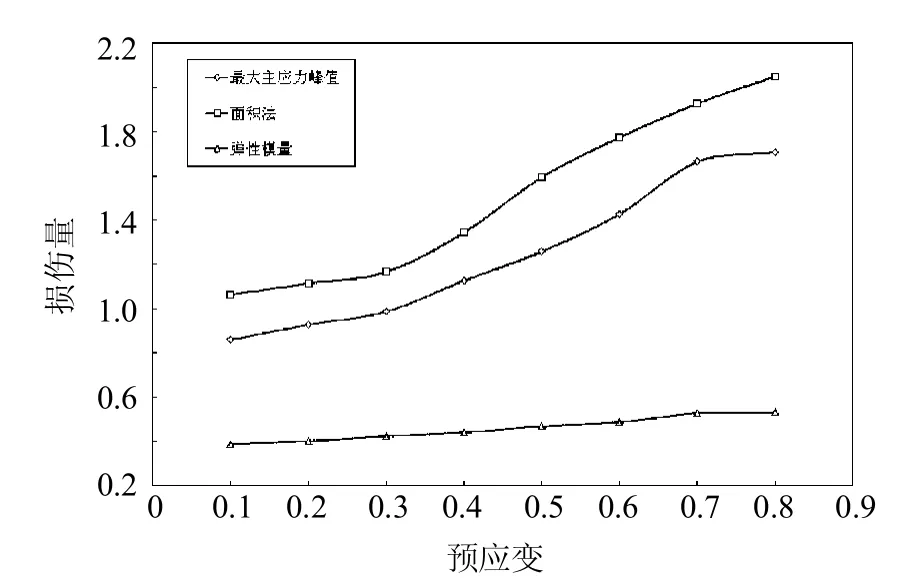
图9 损伤量与预应变关系曲线Fig.9 Curvesof damagesand pre-strains

图10 无量纲化损伤量与预应变关系曲线Fig.10 Curvesof nondimensionaldamagesand pre-strains
从图中可以明显看出3种表示法所显示的规律基本一致,都显示出损伤量随预应变的增加而不断变大;同时,3种损伤量表示的结果在0.1~0.3倍拉伸比预应变范围内,曲线的斜率较低,之后开始逐渐增大,由此可以得到结论,硫化橡胶材料在使用过程中,预应变保持在0.3倍拉伸比以内,可保证材料的损伤程度保持在相对较小的程度.
3 结论
1)在循环加载过程中,硫化橡胶材料对加载速率影响非常敏感,随着加载速率的增加,材料的主应力峰值增大.在低速范围0~100 mm/m in内较为明显,在此区间内主应力峰值随加载速率变化十分剧烈,但当加载速率大于100 mm/m in后,主应力峰值增长较为平缓.不同加载速率下的循环加载中,各循环中损伤量的变化规律基本保持一致,可以看出损伤量随循环次数的改变量受加载速率影响不大;
2)采用应变能密度峰值、面积法及弹性模量法等几种损伤量都可以对橡胶材料的力学性能和损伤量进行表征.对几种损伤参数结果进行对比,弹性模量法可以计算受力过程中任意2时刻之间所产生的损伤,而面积表示法则可以更全面的表征整个加载过程中损伤量的变化.
3)随着预应变的增加硫化橡胶材料的损伤会逐渐加大,并呈非线性变化,当预应变量保持在0.3倍拉伸比以内时,预应变对损伤量的影响不大,当预应变量大于0.3倍拉伸比后,预应变对损伤量的影响就变得十分明显.
[1]Gent A N.橡胶工业 [M].张立群,译.北京:化学工业出版社,2002.
[2]王作龄.橡胶材料科学的发展 [J].世界橡胶工业,1998,25(2):41-47.
[3]桑建兵,邢素芳,刘波,等.橡胶缓冲器及其接触分析 [J].河北工业大学学报,2006,35(1):21-24.
[4]任九生,黄兴.变温下橡胶材料力学性能的实验分析 [J].实验力学,2007,22(6):612-616.
[5]Ecevit Bilgili.Controlling the stress-strain inhomogeneities in axially sheared and radially heated hollow rubber tubes via functional grading[J].MechanicsResearch Communications,2003,30(3):257-266.
[6]黄筑平.连续介质力学基础 [M].北京:高等教育出版社,2003.
[7]Lia J,Mayaub D,LagarrigueV.A constitutivemodeldealingwith damagedue to cavity grow thand theMullinseffectin rubber-likematerialsunder triaxial loading[J].Journalof theMechanicsand Physicsof Solids,2008,56(3):953-973.
[8]刘宇艳,田振辉,万志敏,等.橡胶复合材料在循环载荷下的疲劳损伤特性 [J].橡胶工业,2003,50(12):713-716.
[9]上官文斌,王小莉,叶必军,等.应变比对填充天然橡胶疲劳特性影响的试验及其寿命预测方法研究[J].机械工程学报,2013,49(8):49-56.
[10]王小莉,上官文斌,刘泰凯,等.填充橡胶材料单轴拉伸疲劳试验及疲劳寿命模型研究 [J].机械工程学报,2013,49(14):65-73.
[11]Garnier P,Le Cam J-B,Grédiac M.The influence of cyclic loading conditions on the viscoelastic properties of filled rubber[J].Mechanicsof Materials,2013,56(1):84-94.
[12]MartinRendek,A lexander Lion.Amplitudedependenceof filler-reinforced rubber:Experiments,constitutivemodellingand FEM-Implementation [J].International Journalof Solidsand Structures,2010,47:2918-2936.
[13]GB/T 258-2009,硫化橡胶或热塑性橡胶拉伸应力应变性能的测定 [S].
[责任编辑 田 丰 夏红梅]
The experimentalstudy on effectsof pre-strain in the damage of vulcanized rubbers
LIXiaolei,LIXinye,SANG Jianbing,QIEYanhui,ZHANG Chengbo
(Schoolof Mechanical Engineering,HebeiUniversity of Technology,Tianjin 300130,China)
A cyclic loading testunderuniaxial tension is carried out forvulcanized rubber specimens.Both stress-strain relation curvesof the rubberwereattained undervarious loading ratesand pre-strains.Theeffectsofvarious loading rates and theeffectsofvariouspre-strainsonmechanicalpropertiesof thematerialwere investigated.Based on theexperimental data,the damage properties using some commonly used damage parameters(maximum strain energy density peak, enclosed areaof loading curvesand elasticmodulusmethod)wereanalyzed.The research achievementindicates that the principalstresspeak increaseswith the loading rates.Meanwhile,themechanicalproperty ofvulcanized rubberstabilizes with the increase of cycle index.And the damage ofmaterial increases nonlinearly with the pre-strains.It isalso shown that the vulcanized rubber can achieve good applicationwith the pre-strain ratio under 0.3.
vulcanized rubber;large deformation;damage parameter;experimentalanalysis;pre-strain
O346.5
A
1007-2373(2016)01-0019-08
10.14081/j.cnki.hgdxb.2016.01.004
2015-09-09
河北省自然科学基金(E2011202011,2011202115);天津市自然科学基金(12JCYBJC19600)
李晓雷(1972-),男(汉族),副教授,博士.
数字出版日期:2016-02-27数字出版网址:http://www.cnki.net/kcms/detail/13.1208.T.20160227.1605.002.htm l
