基于BP神经网络游轮预售票定价及升舱方案的研究*

2017-01-06张依一朱家明周文俊

通化师范学院学报 2016年12期

关键词：舱位航次游轮

张依一，朱家明，潘婷，周文俊

(1.安徽财经大学金融学院，安徽蚌埠233030;2.安徽财经大学统计与应用数学学院，安徽蚌埠233030)

基于BP神经网络游轮预售票定价及升舱方案的研究*

张依一1，朱家明2，潘婷2，周文俊2

(1.安徽财经大学金融学院，安徽蚌埠233030;2.安徽财经大学统计与应用数学学院，安徽蚌埠233030)

针对游轮公司预售票定价和开船后升舱方案，建立BP神经网络预测及灰色关联度模型，预测出每次航行各周预订舱位的人数.分析每航次每周预定的平均价格和每航次每周意愿预定人数的关联度，对每周的意愿人数进行合理地赋权，预测出每周预订的平均价格.建立需求定价模型，对售票价格合理定价.游轮起航后，在头等、二等舱位未满的情况下，建立游客升舱模型，使公司获得最大的预期销售收益.

游轮定价;需求定价模型;线性规划;升舱模型;BP神经网络预测

近年来乘坐游轮旅游的人越来越多，游轮公司的发展也非常迅速.如何通过合理的定价吸引更多的旅游者，从而为游轮公司创造更多的收益，是众多游轮公司需要探讨和解决的问题.游轮售票一般采用提前预订的方式进行售票，游轮公司为了获得每次航行的预期售票收益，希望通过历史数据预测每次航行的预定舱位人数和预订舱位的价格，为保证价格的平稳性，需要限定同一航次相邻两周之间价格浮动比，同时需要根据意愿预定人数(填写信息表而未交款的人数)转化为实际预定人数(填写信息表并交款的人数)的多少决定定价方案.

1 数据的获取与假设

本文数据来源于2015年中国电机工程学会杯B题［1］.方便于解决问题，提出如下假设:

①预测期间游轮公司经营状况良好，不存在破产问题;②航行中不存在人为或自然所导致的重大事故;③所有数据均为原始数据，且来源真实可靠.

2 预测每次航行各周预订舱位的人数和价格

对于游轮公司而言，在每次航行前对各周预订舱位的价格的预测十分重要.通过整理分析各航次每周实际预定人数的非完全累积表，在对每次航行各周预定舱位价格的预测上，首先对预定的平均价格进行预处理，剔除误差较大的数据，接着采用BP神经网络模型［2－3］预测每次航行各周预订舱位的人数和价格，最后对模型进行误差分析和合理优化.

2.1 数据处理

(1)采用BP神经网络模型预测每次航行各周预订舱位的人数.

(2)对模型进行误差分析和合理优化.为了使模型得出的结果更为准确作两条限定.①综合每次航行的实际预定总人数，可以确定出每次航行的实际预定总人数的范围，对模拟的数值规定出一个上限，使数据在一定的范围内进行模拟预测.②对于最后几次航行数值缺少较为严重的情况采用分步预测法，比如在预测三等舱第十航次时，先根据第十四周到第六周的数据对第五周的数据进行预测，再根据第十四周到第五周的数据对第四周的数据进行预测，以此类推逐步对每周的数据进行预测.

2.2 结果分析及准确性验证

以各航次每周实际预订人数非完全累积表中第五航次三等舱为例，进行BP神经网络预测并对学习模拟的可靠性进行检验［4－5］，绘制出神经网络学习曲线图，如图1所示.

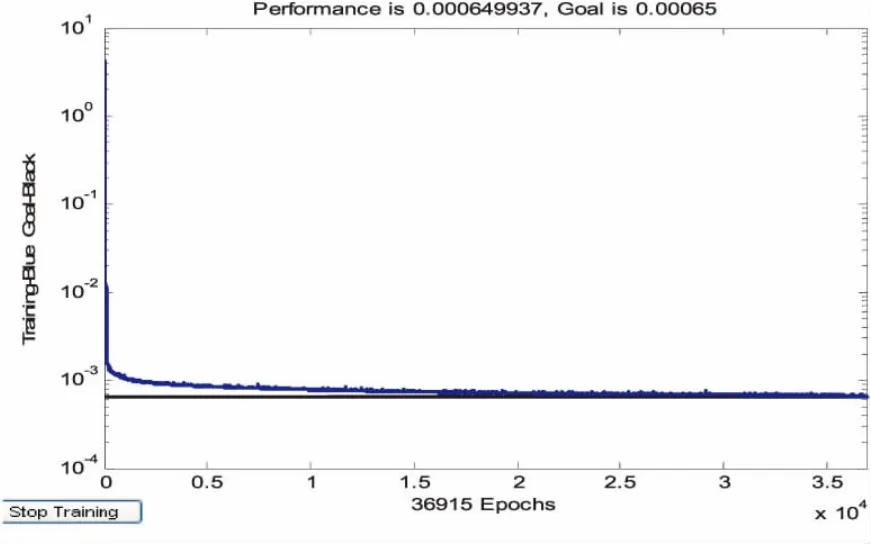
图1 神经网络学习曲线

从图1可以看出，网络训练所得的误差很小.将原始数据仿真的结果与已知样本进行对比测试，用MATLAB自带神经网络工具箱生成的原始数据与仿真数据的对比图，如图2所示，这里的周是指从第几周开始预订(即0表示距航行的周数为14).

图2 原始数据与仿真数据对比

从图2可以看出，实际样本与网络输出值两者之间的图形非常接近，误差值极小.预测出来的结果可信度很高.

从结果看，模型能够反映出数据的变化情况，从对实际情况的网络学习模拟曲线的观察，可以看出改进后的网络训练所得到的误差更小，达到目标值的精度更高.在对第零周的预测时，每次航线航行的实际预定总人数实现了与每次航行的实际预定总人数的绝对吻合，使预测出的数据更具可信度.对各舱每航次每周意愿人数的预测，作出折线图观察它们的变化情况，如图3所示(以头等舱为例).

从图3可以看出，每航次每周预定平均价格和每航次每周意愿预定人数的变化趋势相似，都是先增大后减小，对此游轮公司可以初步确定一个合理的定价方案.

图3 每周预定头等舱的平均价格曲线

3 预测每航次每周意愿预定人数

游轮采用提前预订的方式进行售票.在对每次航行各周预定舱位价格的预测上首先对数据进行预处理，剔除误差加大的数据;接着建立灰色关联度模型［6］，分析每航次每周预定的平均价格和每航次每周意愿预定人数的关联度;最后建立合理的权重模型对每周的意愿人数进行合理赋权，并预测出结果.

供水安全具有相对性，其安全与否归根到底取决于需求的满足程度。供水安全是一种社会存在，安全问题、安全现象、安全风险等本身具有客观性，但供水安全并非是一种完全的自在之物，它又是人类社会心理的产物。供水是否安全，是相对于用水需求的满足程度的，应以人类评价为依据，供水安全的标准也应是相对于人类需求而言的，供水安全存在标准同样说明其不能离开主观评价独立存在。

3.1 基于灰色关联度确定意愿预定人数与平均价格的关联系数

将每航次每周预定平均价格和每航次每周意愿预定人数视为一个整体，即灰色关联系统［7－8］.求出意愿预定人数与平均价格关联系数得出每航次每周预定平均价格和每航次每周意愿预定人数之间有着一个比较大的关联度.

3.2 运用熵值法与变异系数法确定权重并给出预测结果

在对问题的分析中发现，由于采用由加权平均法得到的结果不是很好.所以对权重的处理采用一个更合理的方法，即采用熵值法与变异系数法相结合的组合权重法.

计算权重.

①计算熵值e和信息效用值.计算第j项指标的信息熵值，某项指标的信息效用值取决于该指标的信息熵值e与1之间的差值，它的值直接影响权重的大小，信息效用值越大，对评价的重要性越大，权重也越大.

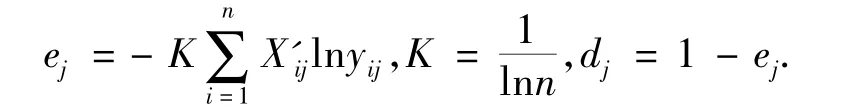
计算评价指标权重，其中权重越大，对评价的重要性也越大.第j项指标的权重为

②变异系数确定权重.对变异系数法的计算同样采用指标“不同舱位每次票价每周意愿预定的人数”，计算各指标的变异系数［3］，其中为第i项指标的平均值是第i项指标的方差，公式为vi=si/||，对vi进行归一化，即得到各指标的权数

③熵值法与变异系数法的组合权重计算方法

⑤平均价格的计算，用组合权重计算出的各舱位每周的预定平均价格.

与原始数据对比可以发现，采用组合权重法得到的结果相对于使用相对加权平均法得到的数据有了一个很大程度上的改进，游轮公司可以根据这一预测方法对预售票进行更为合理的定价.

4 游轮每次航行的最大预期收益下售票定价方案的确定

通过预测得到的每次航行各周预订舱位的人数和价格每航次每周意愿预定人数，可以进一步对游轮公司制定最大预期销售收益模型.为了使游轮公司获得最大预期销售收益，对售票价格在给定区间内合理定价，首先建立需求定价模型［7－8］，以最大收益为目标，建立线性规划问题并用Lingo求得最优解，为了不失一般性，仅考虑一种舱位类型的情况.假定游轮特定舱位的存量为K，销售周期包含T个周.令t=T－1表示第1个周期，t=0表示最后一个周期.也就是t是启航之前的周期个数，t随时间递减.假定游轮旅客的保留价格服从一定的概率分布，且在整个销售周期上是固定不变的，令F(pt)为保留价格的累积概率分布.在每个周期t，企业提供价格F(pt).只有当保留价格低于当前的价格时顾客才会购买，顾客购买舱位的概率为F(pt).Dt(pt)= Mt［1－F(pt)］为周期t的需求函数，其中Mt为周期t的潜在市场规模，价格pt为决策变量.目标是在有限的销售周期［0，T－1］内为不同航次的不同周期确定最优价格，从而最大化整条航线未来的总收益.

4.1 需求定价模型的构建

建立需求函数［9－10］，假设每种舱位每周预定价格在价格区间内服从区间［Vmin，Vmax均匀分布.因此，每个周期的需求函数为

其中Mt为周期t的潜在市场规模，价格pt为决策变量.

根据每个周期的需求函数，为求游轮每次航行的最大预期售票收益，建立单目标线性规划问题模型.

其中第一个约束条件保证临近周期的价格差异不会太大，即游轮每周往返一次，同一航次相邻两周之间价格浮动比不超过20%，这里α取0.2.第二个约束条件是存量约束，保证总需求不会超过游轮的总存量.头等舱位K1=250，二等舱位K2=450，三等舱位K3=500.以第八次航行为例，求解游轮预期销售收益.

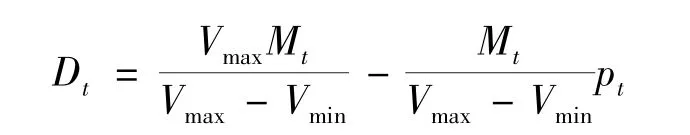
4.2 求解及结果的分析

对于不同舱位，销售的票价不同，实际预订人数不同，销售收益也不同.分别对三个舱位建立最大收益线性规划，通过目标函数和约束条件，利用Lingo求不同舱位每周平均价格的最优解，并计算出最大收益.求解的结果，如表1所示.

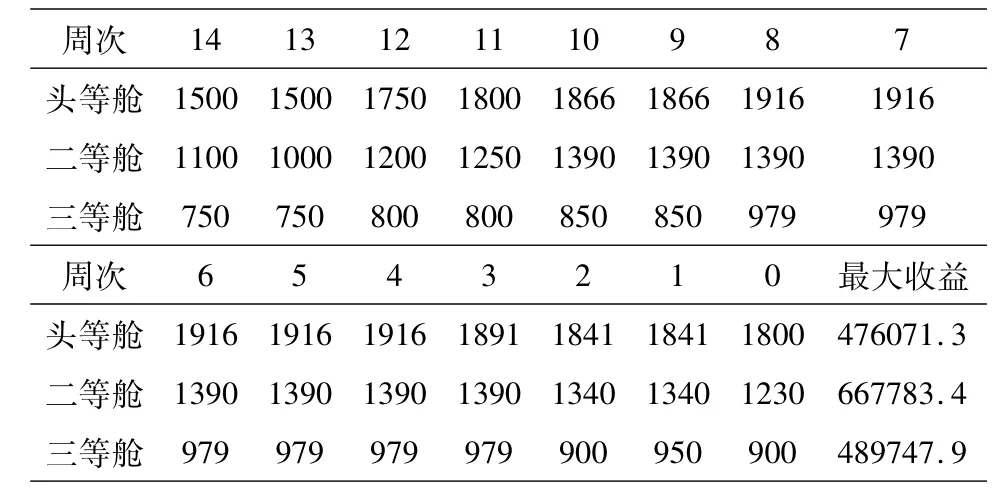
表1 不同舱位每周平均价格

从对表1中数据的分析可以得出，第八次航行头等舱的预期售票收益为476071.3元，二等舱的预期售票收益为667783.4元，三等舱的预期售票收益为489747.9元.游轮公司可以选用该定价模型，这样可以在游轮启航前为公司提供一个合理的定价方案使公司获得更大的收益.

5 公司预期售票收益最大下分析游客的升舱意愿

一般的游轮起航后或多或少会有一些空的舱位，如何利用这些空的舱位获取更多的利润是游轮公司关注的重要问题.这里对较低的舱位进行升舱就是一种很好的选择，(升舱:即原订二等舱游客可通过适当的加价升到头等舱，三等舱的游客也可通过适当的加价升到头等舱、二等舱.)在头等、二等舱位未满的情况下，游客登船后，由于未售出的舱位在游轮启航后的价值为零，这时引导顾客购买价格较高的座位就能够为公司带来较多的收益.

为了使公司预期售票收益最大并且满足游客的需求，建立游客升舱意愿模型.假设升舱价格服从均匀分布，p1，p2，p3分别表示二等舱升头等舱、三等舱升头等舱、三等舱升二等舱的加价价格.p1～U［V1min，V1max］，p2～ U［V2min，V2max］，p3～ U［V3min，V3max］，升舱需求与升舱价格与游客升舱意愿人数有关，建立升舱需求函数:

其中D1(p1)，D2(p2)，D3(p3)分别表示二等舱升头等舱、三等舱升头等舱、三等舱升二等舱的需求.M表示游客升舱意愿人数，它与升舱价格有关，建立线性规划模型:

其中K1，K2表示头等舱、二等舱的客容量，K1= 250，K2=450，N1，N2表示头等舱、二等舱实际预订人数.

在对比分析中可以看出每次航行中实际预订总人数中头等舱，二等舱和三等舱的预订人数占总舱位人数的比率为0.774、0.92、0.989;每次航行升舱后最终舱位人数中头等舱，二等舱和三等舱的预订人数占总舱位人数的比率为0.962、0.926、0.890.对每次航行各舱位的占比进行分析后可以看出，游轮公司为了取得更大的收益，可以在预定售买二，三等舱的舱位时进行一定程度上的超售.

游轮公司通过建立升舱模型可以得到更多的收益，所以游轮公司应该在游客升舱方面进行更好的宣传，对低价票实行超额预订，一旦座位数量不够时，可动员顾客改买高价票，有时候当超售成为实超时，升舱销售会转为免费升舱，由此可以使游轮公司增大利润.

6 总结

本文针对游轮公司预售票的问题利用BP神经网络模型的自我学习能力，对数据进行多输入多输出，实现了对数据的拟合和预测，并对模型的准确性进行了检验及优化，从而对订票的人数和价格进行了合理的预测，但由于优化后的BP神经网络模型对每一数值都要进行MATLAB程序求解，所以运算量较大.在游轮每次航行的最大预期收益下售票定价方案的确定时，对得到的结果进行误差分析，使结果更加合理可行.在对游轮起航后的空舱位制定新的增值方案时，建立游客升舱模型，给出了合理的升舱建议及升舱的具体方案，并对游轮公司的经营提出了合理的建议.解决了游轮公司存在的三方面问题:①可以为邮轮公司预测每次航行前各周内预定舱位人数、预订舱位的价格提供参考，从而使邮轮公司在每次航行前对航行的售票收益有一个准确地预测;②有助于改善邮轮旅游业的商业运营模式，使邮轮旅游业的发展更加合理;③可以为想要投资邮轮旅游业的投资者提供一个较为准确的邮轮旅游业盈利模式.

［1］2015年全国大学生电工数学建模大赛B题赛题下载研究［EB/OL］.(2015－05－29)［2015－10－11］.http://shumo.nedu.edu.cn/

［2］何树红.比较BP神经网络和RBF神经网络在基金净值预测中的应用［J］.云南民族大学学报，2014，23(2):124－127.

［3］王强，汪姚，胡红飒，等.基于BP神经网络算法的风电功率预测［J］.科技和产业，2014(4):143－145.

［4］陈明.MATLAB神经网络原理与实例精解［M］.北京:清华大学出版社，2013.

［5］卓金无.MATLAB在数学建模中的应用［M］.北京:北京航空航天出版社，2011.

［6］强凤娇.灰色聚类决策中指标权重和综合决策测度权系数的确定［J］.统计与决策，2015(22):51－53.

［7］杨秀云，冯根福.民航业的需求差别定价:特点和运用［J］.经济科学，2003(5):45－47.

［8］钱浩，刘元志.游轮定价方案研究［J］.现代商业，2015，28 (7):69－70.

［9］杨桂元.数学建模［M］.上海:上海财经大学出版社，2015.

［10］田俊峰，孙西秀，杨梅.考虑需求与价格——质量相关的补货与定价联合决策广义模型［J］.物流工程与管理，2014(5):189－191.

(责任编辑:陈衍峰)

O29