轻型客车复合材料板簧模态的预测和分析

史文库， 钱 琛, 柯 俊， 高 博， 李国民， 袁 可

(1.吉林大学 汽车仿真与控制国家重点实验室，长春 130022；2.宁波华翔汽车零部件研发有限公司，宁波 3150332； 3. 南京依维柯汽车有限公司，南京 210028)

轻型客车复合材料板簧模态的预测和分析

史文库1， 钱 琛1, 柯 俊1， 高 博1， 李国民2， 袁 可3

(1.吉林大学 汽车仿真与控制国家重点实验室，长春 130022；2.宁波华翔汽车零部件研发有限公司，宁波 3150332； 3. 南京依维柯汽车有限公司，南京 210028)

为了预测某轻型客车复合材料板簧的模态并预判复合材料板簧的模态是否会与相关激励耦合发生共振，在ABAQUS软件中建立了针对复合材料板簧模态计算问题的有限元模型。对复合材料板簧的有限元模型进行了计算模态分析，根据计算模态分析结果预测了复合材料板簧的模态。对复合材料板簧的样件进行了试验模态分析，通过对比模态预测结果和试验模态分析结果的方法验证了模态预测结果的准确性和有限元模型的正确性。根据复合材料板簧的模态分析结果，设计的复合材料板簧能够避免共振现象的发生。利用经过验证的复合材料板簧有限元模型分析了各设计变量与复合材料板簧一阶模态频率之间的关系。分析结果表明，选用0°铺层角度、较低密度的复合材料和较高的纤维体积含量能够降低复合材料板簧发生共振的可能性。得到的研究结果可显著降低复合材料板簧的研发风险和成本。

客车；复合材料；板簧；有限元分析；模态分析

随着环境危机和能源危机的日益严重，汽车轻量化已经成为汽车发展的重要方向。与钢板弹簧相比，复合材料板簧的重量可降低50%～70%，疲劳寿命至少是钢板弹簧的两倍，有利于降低汽车的油耗和排放，对汽车的舒适性和安全性都有明显的提升作用。因此，复合材料板簧成为了国内外学者竞相研究的热点领域[1-5]。在汽车行驶过程中，复合材料板簧会受到路面、发动机等产生的振动激励。如何在复合材料板簧开发初期准确预测复合材料板簧的模态，并使复合材料板簧的固有频率避开外界激励的频率范围，最终避免复合材料板簧与外界激励耦合发生共振，这对保证复合材料板簧的疲劳寿命及整车的NVH性能均具有重要的意义。

目前，对复合材料板簧的研究主要集中在复合材料板簧的结构优化、接头设计和疲劳性能方面[6-13]，与复合材料板簧模态相关的研究很少。KRALL等[14]采用锤击法和谱分析法对碳纤维复合材料板簧进行了模态试验，并对碳纤维复合材料板簧的模态进行了理论计算。其研究结果表明，锤击法可更准确地测试复合材料板簧的模态。该报道提出了一种针对复合材料板簧模态的Euler-Bernoulli梁理论，但没有给出可操作的计算方法，且该理论没有体现出复合材料的各向异性，是否适用于变截面复合材料板簧的模态计算还存在疑问。SURESHKUMAR等[15]通过试验发现复合材料板簧的模态频率是钢板弹簧的两倍，说明复合材料板簧与激励耦合发生共振的可能性较小。管鸣等[16]对形状记忆合金复合材料板簧进行了计算模态分析，研究了温度、SMA纤维含量对复合材料板簧的固有频率以及模态振型的影响，但没有对铺层角度等关键参数进行讨论，相关结论也缺乏试验的支持。综上所述，国内外已经对复合材料板簧进行过模态试验，并采用有限元方法进行过计算模态分析。但是，仍然缺乏针对变截面复合材料板簧模态的有效预测方法，关键铺层参数、工艺参数与复合材料板簧模态之间的关系还需要进一步的明确和验证。

针对上述问题，本文首先建立了针对变截面复合材料板簧模态分析问题的有限元模型，利用该模型进行计算模态分析，预测了某轻型客车复合材料板簧的模态。然后，对复合材料板簧样件进行了试验模态分析。通过对比模态预测结果和试验模态分析结果验证了有限元模型的正确性和模态预测结果的准确性，并评价了复合材料板簧的动态性能。然后，利用经过验证的复合材料板簧有限元模型研究了铺层角度、材料密度及纤维体积含量对复合材料板簧一阶模态频率的影响，并得到了有价值的结论，为类似研究提供参考。

1 某轻型客车复合材料板簧简介

若复合材料板簧的刚度、强度等基本性能达不到要求，研究复合材料板簧的模态是没有意义的。因此，在对某轻型客车复合材料板簧的模态进行系统研究之前，需要对复合材料板簧的总成结构和铺层方案进行匹配设计，并进行样件试制和台架试验，以确定其质量、刚度、强度、抗蠕变性能和疲劳寿命等关键性能满足设计目标。限于篇幅，上述研究工作将在其他论文中系统阐述。经过系统的匹配计算及试验，确定某轻型客车复合材料板簧的结构如图1所示。其中，复合材料簧身采用E玻璃纤维增强聚氨酯基复合材料制作，各铺层的铺层角度均为0°。

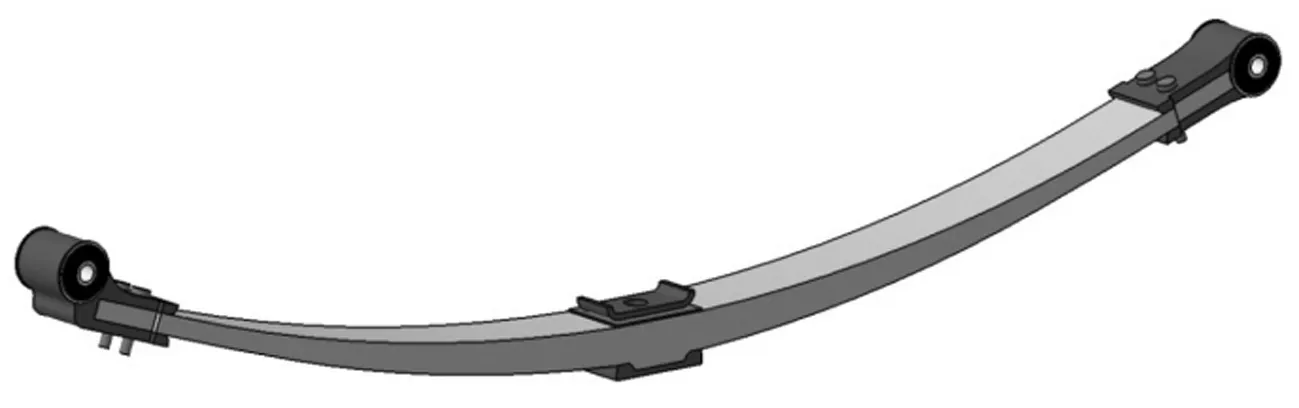
图1 复合材料板簧的结构Fig.1 Structure of composite leaf spring

2 复合材料板簧模态的预测方法

2.1 复合材料板簧模态预测模型的建立

纤维增强树脂基复合材料是典型的非线性材料，具有各向异性及黏弹性，显然这对复合材料板簧的实际模态有一定的影响。然而，在模态分析中，材料的非线性特性将被忽略，即使指定了非线性单元，也将被视作线性单元来处理。因此，在有限元建模过程中只能考虑复合材料的各向异性，这与树脂基复合材料的实际力学性能有一定的差异。但是，如果模态预测结果与试验模态分析结果的误差可以接受，那么这种简化就可认为是合理的。

首先，将复合材料板簧的三维几何模型导入ABAQUS软件中，建立部件和装配件。然后，在Property模块中，定义复合材料和金属部件材料的力学性能。其中，复合材料簧身采用E玻璃纤维/聚氨酯复合材料制作，材料性能参数如表1所示。金属部件采用40Cr钢制作，弹性模量为206 000 Mpa，泊松比为0.3，密度为7.9 g/cm3。在Property模块中，为了体现复合材料的各向异性，采用工程常数的方式定义E玻璃纤维/聚氨酯复合材料的力学性能，通过composite layup manager对话框定义复合材料板簧的铺层参数。其中，铺层方向的定义直接影响模态预测结果的准确性。由于各铺层是沿板簧圆周方向铺设的，具有一定的曲率，因此应在composite layup manager对话框中按照discrete method方式定义铺层方向，选定簧身上表面外法线方向为铺层坐标系的Z轴，簧身上表面边线为铺层坐标系的X轴。需要说明的是，复合材料板簧的铺层设计方案已经通过台架试验的验证，因此利用此有限元模型得到的刚度、强度等仿真结果与样件的性能是基本一致的。

然后，在Step模块建立一个线性摄动载荷步：Frequency，设定采用Lanczos法求解，频率计算范围设置为0～1 024 Hz。此外，在Interaction模块中，根据实际装配关系建立各金属部件与复合材料簧身的绑定约束。最后，在Mesh模块对模型进行网格划分。为了保证计算精度，全部利用六面体单元来对模型进行离散，单元类型为C3D8R。建立的复合材料板簧有限元模型如图2所示，模型共有140 784个单元和167 861个节点。最后，将建立的有限元模型提交ABAQUS的求解器进行计算。

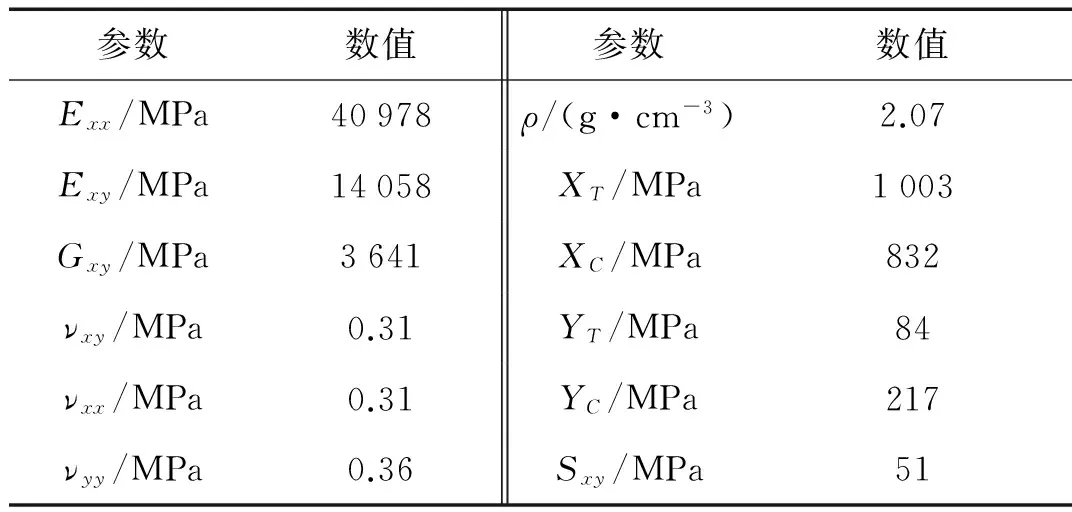
表1 E玻璃纤维/聚氨酯复合材料的力学性能参数Tab.1 Mechanical properties of E-glass/polyurethane

图2 复合材料板簧的有限元模型Fig.2 FEA model of composite leaf spring

2.2 复合材料板簧模态的预测结果

计算完成后，利用ABAQUS的后处理模块对计算结果进行后处理，得到的模态预测结果如图3所示。需要说明的是，复合材料板簧在服役过程中的振动激励主要为低频激励，且大部分来源于竖直方向，应主要关注复合材料板簧的低阶振型和竖直弯曲振型。因此，图3只给出了复合材料板簧的四个关键计算模态振型，其中图3(a)～(c)为计算模态分析得到的前三阶振型，图3(d)为三阶竖直弯曲振型，其模态频率已高达528.56 Hz。计算模态分析还得到了复合材料板簧的其他振型，研究意义不大，限于篇幅本文未列出。

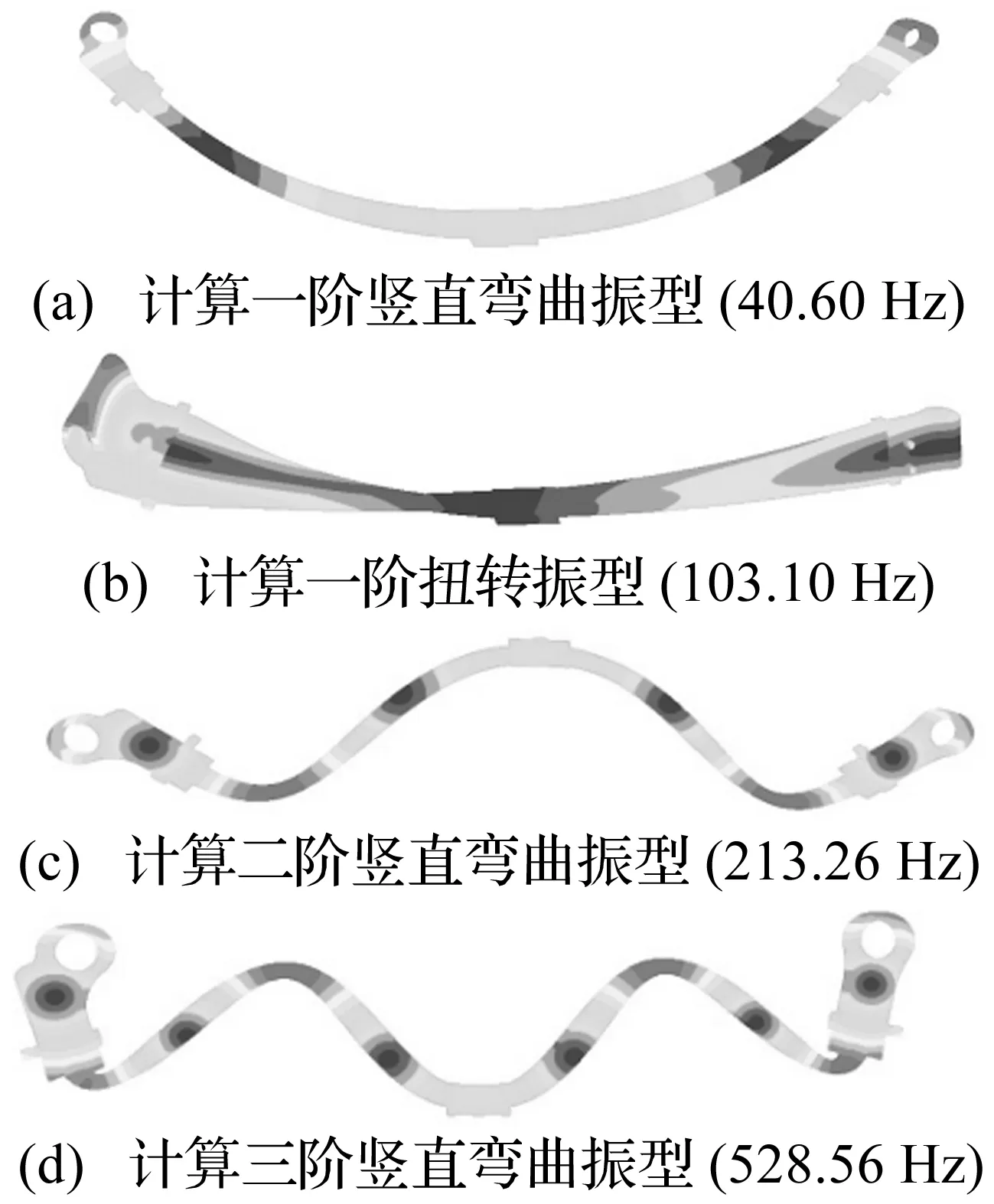
图3 复合材料板簧模态的预测结果Fig.3 Predict results for the modal of composite leaf spring

3 复合材料板簧模态预测结果的验证

3.1 复合材料板簧的试验模态分析

为了获取复合材料板簧样件的模态，通过刚度可忽略不记的橡皮绳对复合材料板簧样件进行整体悬挂，如图4所示。复合材料板簧的尺寸较小，且根据KRALL S和ZEMANN R的研究结果，锤击法可更准确地测试复合材料板簧的模态，因此采用锤击法来对复合材料板簧样件进行试验模态分析。试验采用LMS TEST.LAB测试系统和B&K/PCB公司的三向振动加速度传感器。传感器布置位置和锤击点分别如图5所示，其中椭圆标示为力锤锤击点，立方体标示为传感器布置位置。为了更合理地展示复合材料板簧的试验模态振型，传感器的布置位置参考了计算模态分析的结果，将传感器都布置在复合材料板簧的上表面，分两排沿簧身纵向均匀布置。由于复合材料板簧中部需要预留锤击区域，且端部的金属接头表面与簧身上表面不共面，布置传感器比较困难，因此未在复合材料板簧中部和端部布置加速度传感器，但不影响试验模态振型的展示。由于三向振动加速度传感器数量有限，利用同一组三向振动加速度传感器分别采集不同布置区域的试验信号，再利用LMS软件对试验信号进行合成处理。试验照片如图6所示。

图4 复合材料板簧的悬挂状态Fig.4 Suspend state of composite leaf spring

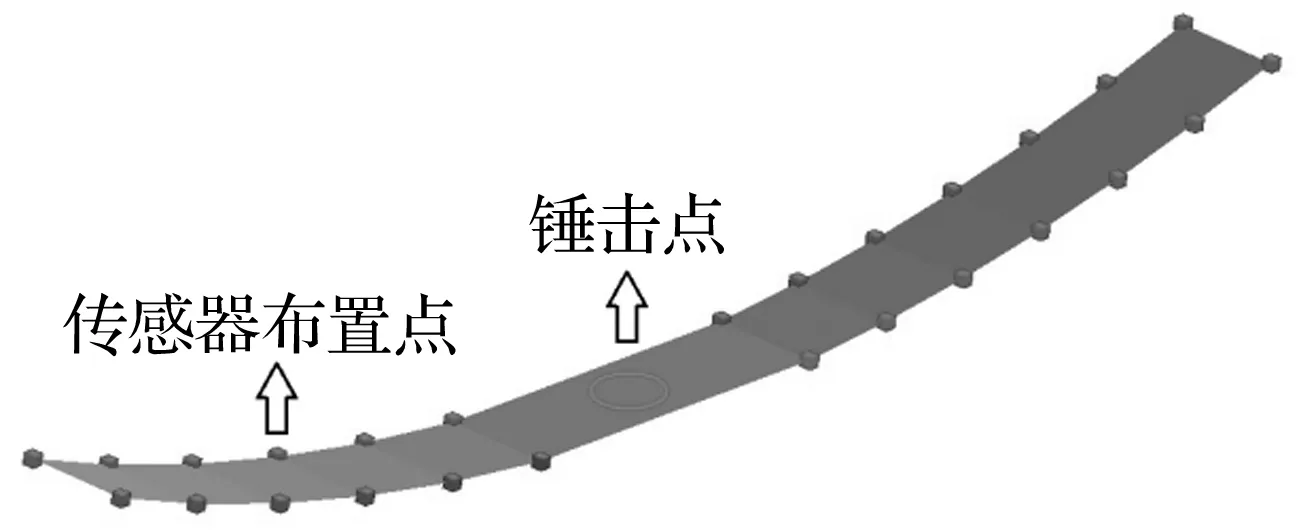
图5 传感器布置点和锤击点示意图Fig.5 Locations of accelerometers and excitation

图6 试验中的锤击状态Fig.6 Hammering state in the test

利用LMS TEST.LAB软件的Polymax模块对试验数据进行后处理，得到的试验模态分析结果如图7所示。

试验过程如下：首先在LMS TEST.LAB软件中建立包含测点坐标等几何元素的几何模型，并在通道设置界面设置相关参数，读取传感器灵敏度并建立测点和通道之间的关联。然后进行锤击示波设置通道量程，并通过锤击试验设置触发级、带宽、加窗及驱动点，其中带宽设置为1 024 Hz。最后，在Measure模块进行测试并采集试验信号。

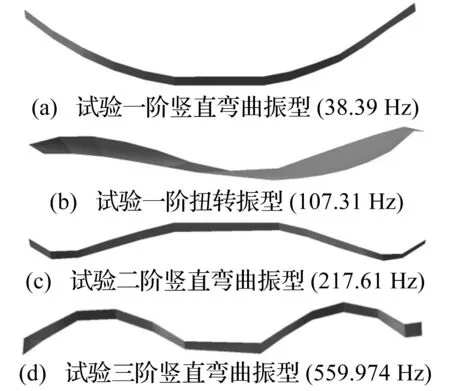
图7 复合材料板簧的试验模态分析结果Fig.7 Results of experimental model analysis for composite leaf spring

3.2 模态预测方法及模型正确性的验证

有限元模型的外形相对逼真，通过计算模态分析能够更加形象地展示复合材料板簧的模态，并从理论角度预测复合材料板簧的模态，但可信度较低。而试验模态分析采集的测点有限，导致模型的外形与样件实际外形有显著的差别，但可信度较高。因此，计算模态分析和试验模态分析的结果可以相互验证，并取长补短，最终确定复合材料板簧的模态。

分别通过计算模态分析预测和试验模态分析获得的复合材料板簧各阶模态频率的对比如表2所示。

表2 模态频率的预测值和试验值的对比Tab.2 Comparison between predict model frequency and test model frequency

根据表2，各关键模态的预测频率与试验频率之间的误差均低于6%。对比图3和图7，各关键模态的预测振型与试验振型基本吻合。因此，模态预测结果基本上反映了复合材料板簧样件的真实模态，说明忽略复合材料的非线性特性对复合材料板簧计算模态分析结果的准确性影响不大，且复合材料板簧的有限元模型是正确的。复合材料板簧的计算模态分析早于试验模态分析，可同时证明复合材料板簧样件的模态得到了准确的预测。

4 复合材料板簧动态性能的评价和模态影响因素分析

4.1 复合材料板簧动态性能的评价

评价复合材料板簧动态性能的目的是考察复合材料板簧的模态能否避开外界激励的频率范围，最终避免复合材料板簧与外界激励耦合发生共振。由于复合材料板簧服役过程中的外界激励主要为低频激励，因此评价复合材料板簧动态性能的好坏主要看其低阶模态，尤其是一阶模态。根据复合材料板簧的试验模态分析结果，其前三阶振型的固有频率分别为38.39 Hz、107.31 Hz和217.61 Hz。

汽车在行驶过程中与板簧有关的振动激励分为路面激励、车轮不平衡激励、发动机激励及传动轴不平衡激励。下面分别进行分析：

(1)路面激励：由道路条件及车速决定。当汽车在较好路面上正常行驶时，激励频率多为1～3 Hz；在高速公路上高速行驶时，路面激励可达到15 Hz左右。复合材料板簧的一阶模态频率远高于15 Hz，因此不存在与路面激励耦合发生共振的可能性。

(2)车轮不平衡激励：因车轮不平衡引起的激励频率一般低于11 Hz，远低于复合材料板簧的一阶模态频率，因此不存在与车轮不平衡激励耦合发生共振的可能性。

(3)发动机激励：此激励对复合材料板簧影响较大。四冲程发动机激振频率计算公式为：

(1)

式中，M为发动机的气缸数目，n为发动机转速(r/min)。某轻型客车采用四缸发动机，怠速转速为800 r/min，按式(1)计算出激振频率为26.7 Hz；空调开启时，怠速转速为850 r/min，则激振频率为28.3 Hz。复合材料板簧的一阶模态频率远高于28.3 Hz，因此复合材料板簧与发动机激励耦合的可能性很小。

(4)传动轴不平衡激励：参考某轻型客车传动轴的模态试验结果，传动轴的一阶固有频率在100 Hz以上，且复合材料板簧的模态频率均避开了传动轴的固有频率。因此，不存在复合材料板簧与传动轴不平衡激励耦合发生共振的可能性。

除了避开外界激励的频率范围，还应使复合材料板簧的模态频率避开簧载质量及非簧载质量的固有频率，以防止其耦合发生共振。试验测得满载状态下某轻型客车后悬架簧载质量偏频为1.72 Hz，非簧载质量偏频为12.12 Hz，空载状态下对应的偏频稍高，但均远低于复合材料板簧的一阶模态频率。因此不存在复合材料板簧与簧载质量和非簧载质量耦合发生共振的可能性。

综上所述，某轻型客车的复合材料板簧不存在与外界激励及其他零部件发生共振的可能性，动态性能良好。

4.2 复合材料板簧模态影响因素分析

虽然某轻型客车的复合材料板簧不存在发生共振的可能性，但在其他车型的复合材料板簧开发后期，若复合材料板簧的一阶模态频率过低并导致共振的现象，将严重威胁复合材料板簧的实际应用，导致研发周期和成本急剧上升。为了避免这一现象，除了需要在开发初期准确预测及评价复合材料板簧设计方案的模态性能外，还需要在设计过程中规避对复合材料板簧模态不利的设计因素，防止共振的发生。因此，本节对复合材料板簧一阶模态的影响因素进行了系统分析。

根据模态分析理论，复合材料板簧的模态从根本上取决于复合材料板簧的结构、质量和刚度等固有特性。结构方面，为了保证与钢板弹簧的互换性及本身的可靠性，复合材料板簧的主要结构及尺寸不宜变动。质量方面，在结构及尺寸不变的情况下，主要取决于复合材料的密度。刚度方面，在结构及尺寸不变的情况下，主要取决于复合材料板簧的铺层方案，包括铺层角度的选择、纤维体积含量及铺层数量的确定。然而，除了模态之外，复合材料板簧的性能指标还包括强度、刚度等。铺层数量对复合材料板簧的刚度、强度等性能指标有非常显著的影响，应主要由复合材料板簧的刚度匹配目标来决定；小部分铺层中铺层角度的改变对复合材料板簧的刚度、强度等性能指标也有一定的影响，但影响作用有限，这种小幅度的性能波动在工程上是可以接受的。纤维体积含量方面，纤维体积含量越高，纤维增强复合材料的力学性能越好。但纤维体积含量越高，对模具及工艺的要求就越高，应主要由工艺及生产条件确定，所以纤维体积含量只能进行小幅度的调整。综上所述，考虑到工程实际，虽然影响复合材料板簧模态的因素很多，但大部分影响因素主要基于复合材料板簧其他性能及工艺条件来考虑，可以单独考虑的设计变量只有复合材料密度、铺层角度及纤维体积含量，且需在设计初期就加以确定。由于复合材料板簧一阶模态频率的高低在很大程度上决定了复合材料板簧与外界激励耦合发生共振的概率，且上述复合材料板簧有限元模型的正确性已经得到验证，因此可通过调整模型中的相关参数并进行计算模态分析的方法来研究相关设计因素对复合材料板簧一阶模态频率的影响。下面分别予以说明：

(1)铺层角度对一阶模态频率的影响

为了方便批量生产并控制制造成本，复合材料板簧实际使用的铺层角度只有0°、45°和90°，因此只讨论这三个角度即可。通过composite layup manager对话框改变复合材料板簧的部分铺层角度，并计算模型对应的一阶模态频率，计算结果如图8(a)所示。图中横坐标代表复合材料板簧中被45°铺层或90°铺层取代的铺层数目，纵坐标代表模型的一阶模态频率。需要说明的是，复合材料板簧之前全部采用0°铺层，图8(a)中横坐标0处对应的点即为全0°铺层对应的复合材料板簧一阶模态频率，如图中箭头标志所示。根据图8(a)，复合材料板簧的一阶模态频率随着全0°铺层中45°或90°铺层的增多有下降的趋势，且90°铺层的下降幅度大于45°铺层的下降幅度。这说明采用0°铺层后复合材料板簧的一阶模态频率最高。因此，为了降低复合材料板簧发生共振的概率，应尽量采用0°铺层。

(2)复合材料密度对一阶模态频率的影响

改变复合材料的材料密度，并计算模型对应的一阶模态频率，计算结果如图8(b)所示。图中横坐标代表复合材料密度的改变量，纵坐标代表模型的一阶模态频率。根据图8(b)，模型的一阶模态频率随着复合材料密度的增大而逐渐降低，这说明为了降低复合材料板簧发生共振的概率，应选用较低密度的复合材料来制作复合材料板簧。用来制造复合材料板簧的基体材料主要有环氧树脂和聚氨酯树脂，两者密度相近，但聚氨酯树脂具有更好的韧性，因此应选择聚氨酯树脂作为复合材料板簧的基体材料；用来制造复合材料板簧的纤维增强材料主要有玻璃纤维和碳纤维。碳纤维的密度明显比玻璃纤维小，因此从模态性能方面考虑，应选用碳纤维作为复合材料板簧的纤维增强材料。

(3)纤维体积含量对一阶模态频率的影响

对于0°铺层而言，纤维体积含量的影响主要体现在0°铺层的纵向拉伸模量。纤维体积含量越高，0°铺层的纵向拉伸模量就越高。因此，改变0°铺层的纵向拉伸模量，并计算模型对应的一阶模态频率，计算结果如图8(c)所示。图中横坐标代表材料纵向拉伸模量的改变量，纵坐标代表模型的一阶模态频率。根据图8(c)，模型的一阶模态频率随着纵向拉伸模量的增大而逐渐增大，这说明为了降低复合材料板簧发生共振的概率，应选用较高的纤维体积含量。综合考虑力学性能及工艺条件，复合材料板簧的纤维体积含量一般为50%～65%。从模态性能方面考虑，应将纤维体积含量取为较高的60%～65%，具体值根据工艺条件及树脂的浸润效果来综合确定。

图8 模型一阶模态频率与设计变量之间的关系Fig.8 Relationship between first order modal frequency of model and design variables

5 结 论

(1)提出的复合材料板簧建模及模态计算方法可以准确地预测复合材料板簧的模态，从而显著降低复合材料板簧的开发风险和成本。

(2)根据复合材料板簧的模态分析结果，设计的复合材料板簧能够避免共振现象的发生。

(3)选用0°铺层角度、较低密度的复合材料(推荐选用碳纤维增强聚氨酯基复合材料)和较高的纤维体积含量(推荐选用60%～65%)可提高复合材料板簧的一阶模态频率，降低复合材料板簧发生共振的概率，可为类似工程问题提供参考。

[1] BEARDMORE P, JOHNSON C F. Potential for composites in structural automotive applications [J]. Composites Science and Technology, 1986, 26(4):251-281.

[2] AL-QURESHI H A. Automobile leaf springs from composite materials [J]. Journal of Materials Processing Technology,2001, 118(1/2/3):58-61.

[3] MAHDI E, ALKOLES O M S, HAMOUDA A M S，et al. Light composite elliptic springs for vehicle suspension [J]. Composite Structures, 2006, 75(1/2/3/4):24-28.

[4] HOU J P, CHERRUAULT J Y, JERONIMIDIS G，et al. Design, testing and simulation of fiber composite leaf springs for heavy axle load [J]. Journal of Strain Analysis for Engineering Design，2005，40(6): 497-504.

[5] RAJENDRAN I，VIJAYARANGAN S. Design, analysis, fabrication and testing of a composite leaf spring [J]. Journal of the Institution of Engineers(India): Mechanical Engineering Division，2002，82(3):180-187.

[6] SANCAKTAR E, GRATTON M. Design, analysis, and optimization of composite leaf springs for light vehicle applications[J].Composite Structures,1999,44(2/3):195-204.

[7] SUBRAMANIAN C, SENTHILVELAN S. Joint performance of the glass fiber reinforced polypropylene leaf spring [J]. Composite Structures, 2011, 93(2):759-766.

[8] SHOKRIEH M M, REZAEI D. Analysis and optimization of a composite leaf spring [J]. Composite Structures, 2003,60(3): 317-325.

[9] RAJENDRAN I, VIJAYARANGAN S. Optimal design of a composite leaf spring using genetic algorithms [J]. Computers and Structures, 2001, 79(11): 1121-1129.

[10] FERREIRA J A M, COSTA J D M, REIS P N B, et al. Analysis of fatigue and damage in glass-fibre-reinforced polypropylene composite materials [J].Composites Science and Technology, 1999, 59(10): 1461-1467.

[11] FERREIRA J A M, COSTA J D M, REIS P N B. Static and fatigue behavior of glass-fibre-reinforced polypropylene composites[J].Theoretical and Applied Fracture Mechanics,1999,31(1): 67-74.

[12] KUMAR M S, VIJAYARANGAN S. Analytical and experimental studies on fatigue life prediction of steel and composites multi-leaf spring for light passenger vehicles using life data analysis [J]. Materials Science-Medziagotyra，2007，13(2): 141-146.

[13] KUEH J T J, FARIS T. Finite element analysis on the static and fatigue characteristics of composite multi-leaf spring [J]. Journal of Zhejiang University：Science A ，2012，13(3):159-164.

[14] KRALL S, ZEMANN R. Investigation of the dynamic behavior of CFRP Leaf Springs[C]// Procedia Engineering.24th DAAAM International Symposium on Intelligent Manufacturing and Automation. Zadar：Elsevier Ltd，2015:646-655.

[15] SURESHKUMAR M, TAMILSELVAM P, KUMARAVELAN R，et al. Design，fabrication and analysis of a hybrid fiber composite monoleaf spring using carbon and E-glass fibers for automotive suspension applications[J]. Mechanics of Composite Materials，2014，50(1)：115-122.

[16] 管鸣，任勇生，孙祥正. 基于ANSYS的形状记忆合金复合材料板簧的模态分析[J].山东科技大学学报(自然科学版)，2012，31(6):106-112. GUAN Ming，REN Yongsheng，SUN Xiangzheng. Modal analysis of composite leaf spring with SMA based on ANSYS[J]. Journal of Shandong University of Science and Technology(Natural Science)，2012，31(6):106-112.

Prediction and analysis for the modal of a composite leaf spring in a light bus

SHI Wenku1, QIAN Chen1, KE Jun1, GAO Bo1，LI Guomin2， YUAN Ke3

(1. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China; 2. Ningbo Huaxiang Automotive Research and Development Co., Ltd.，Ningbo 315033, China；3. Nanjing Automobile Group Co., Ltd.，Nanjing 210028, China)

In order to predict the modal of a composite leaf spring in a light bus and determine if the resonances among the modal of the composite leaf spring and the excitations will occur or not，the finite element model for the modal analysis of the composite leaf spring was established by using ABAQUS software. The computational modal analysis for the finite element model was carried out and the modal of the composite leaf spring was predicted according to the result from computational modal analysis. Then the experimental modal analysis for the prototype of the composite leaf spring was performed. The veracity of the prediction modal and the correctness of the finite element model were validated by the comparison between the prediction modal and the results of the computational modal analysis. According to the modal analysis results，the composite leaf spring could avoid resonances. The relationships among design variables and the first-order modal frequency of the composite leaf spring were analyzed respectively by using the finite element model，which has been validated. The analysis results indicate that 0° ply orientation， composite with lower density and higher fiber volume content can reduce the possibility of resonances. The research results can significantly reduce the risk and the cost in the development of composite leaf springs.

bus; composite; leaf spring; finite element analysis; modal analysis

国家自然科学基金资助项目(51205158);中国博士后科学基金面上资助项目(2013M541294);吉林省重大科技专项(212E362415);吉林大学研究生创新项目(450060503159)

2015-05-19 修改稿收到日期：2015-12-05

史文库 男，博士，教授，博士生导师，1960年10月生

柯俊 男，博士生，1989年2月生

U463.33+4.7

A

10.13465/j.cnki.jvs.2016.24.023