一种宽频压电能量收集装置的建模与实验研究

刘少刚， 程千驹， 赵 丹， 冯立锋

(哈尔滨工程大学 机电工程学院，哈尔滨 150001)

一种宽频压电能量收集装置的建模与实验研究

刘少刚， 程千驹， 赵 丹， 冯立锋

(哈尔滨工程大学 机电工程学院，哈尔滨 150001)

为拓宽振动压电能量收集装置工作频带宽度，提出一种新型两自由度分段线性能量收集结构，同时为便于未来对该装置进一步的关键参数优化与微小型设计，提出该结构的理论模型并给出解析解结果，通过对实验样机加工与实验平台搭建得到所提出装置发电性能实验结果。对比理论值与实验值表明，所提出装置在第一共振区间与第二共振区间的工作频带宽度分别为2.2 Hz与4.5 Hz，总频带宽度达到6.7 Hz，与相对应两自由度线性系统比较，其拓宽效果达到4.78倍。在误差允许范围内，装置发电性能解析解结果与实验值基本保持一致，所提出装置能够有效拓宽发电工作频带宽度。

分段线性；两自由度；拓宽频带；压电；能量收集

近年来集成电路的快速发展大大减小了微电子元器件的能量损耗，同时由于传统的电池供能所具有的寿命短及更换程序复杂等缺点，收集环境中的清洁能源为微机电系统供能的研究受到越来越广泛的关注[1-5]。相对于其他能量如太阳能、热能而言，振动能具有无处不在的优点，使其成为能量收集最有潜力的能量来源。为实现对振动能量的收集，目前主要有三种能量转换机制，分别为磁电转换[6]、静电转换[7-10]及压电转换[11-17]，其中压电转换机制以其结构紧凑，转换效率高等优势，成为振动能量收集研究的热点。

振动压电能量收集系统通常以悬臂梁贴附压电片的结构形式出现。类似结构在对振动能收集的过程中，通常只在很窄的频带上产生峰值电压，一旦激振频率偏离装置的共振频率，系统的发电电压幅值就会急剧下降以至无法输出足够能量供微电子元器件使用。由于环境中大多数振动源的频率会在一个区间内变化，因而上述情况严重制约了振动能量收集装置的发电性能，为了解决这个问题，很多研究通过引入磁力，机械力等作为非线性恢复力拓宽系统发电频率[18]。其中，通过引入撞块，将悬臂梁振动由线性振动改变为分段线性振动，十分有效地拓展了装置的工作频带宽度。然而，此类装置的研究目前仅局限于单自由度系统，迄今尚无针对分段线性多自由度能量收集系统的研究。因此，本文提出两自由度分段线性能量收集系统机电耦合模型，并通过理论与实验两方面研究，验证了该装置具有拓宽系统发电频带宽度的性能。

1 工作原理及理论建模

所提出两自由度分段线性能量收集装置的结构简图如图1所示。装置由一个两自由度主悬臂梁和一个单自由度从动悬臂梁组成。作为能量转换部件的压电片贴附于两自由度主梁的第一段梁上，位于主梁的中部与顶端的质量块将作为振动质量。质量块1与从动梁之间有距离为d的间隙，当基座处的外部激振足够大时，由于质量块在每个振动周期中的位移大于间隙距离d而与从动梁发生碰撞作用。因此，系统此时每个周期的运动状态分为两部分，即碰撞前与碰撞后，系统整体运动状态呈分段线性振动状态，其也属于非线性振动中的一种特殊情况。

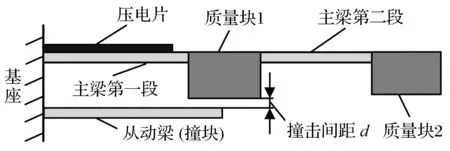
图1 两自由度分段线性压电能量收集装置结构简图Fig.1 Geometric construction of the proposed two-degree-of-freedom piecewise-linear energy harvester

为方便对系统进行理论建模，其等效集中参数模型如图2所示。图中，参数m1和m2分别表示主梁上的振动质量，系数k1,k2分别为主梁两段梁的等效刚度，两段梁的等效阻尼表示为c1,c2。由于相对振动质量m1而言，从动梁的质量可以忽略不计，从动梁可等效为弹性系数k3以及阻尼系数c3。当装置基座受到谐波信号z0(t)作用时，振动质量m1和m2将跟随基座一起振动，其振动位移表示为z1(t)及z2(t)。对应于上文提到的碰撞前与碰撞后系统的两部分运动状态，往复位移z1(t)和z2(t)分为两个阶段：第一阶段为振动质量m1与从动梁之间的相对位移小于间隙d时，第一段梁的等效刚度与等效阻尼保持k1及c1不变；第二阶段为振动质量m1与从动梁之间的相对位移大于间隙d时，由于振动质量m1与从动梁发生碰撞而带动从动梁一起振动，首段梁的等效刚度与等效阻尼将发生改变，其值将由原来的k1和c1变为k1+k3和c1+c3。

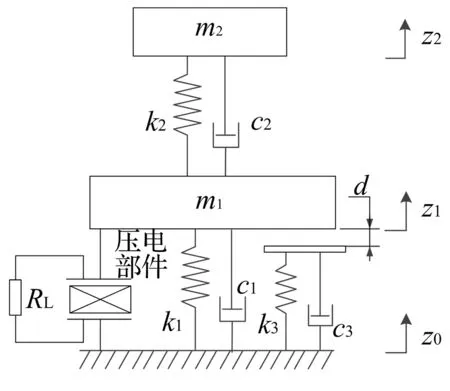
图2 所提出装置等效集中参数模型Fig.2 Spring-mass-damper model of the proposed device

设y0=z0、y1=z1-z0及y2=z2-z1，图2所对应的运动学方程可简化为:

(1)

式中:z0(t)=Zcos(ωt),Z表示激励信号位移的振幅，ω表示激励信号频率,v表示负载电阻RL两端的电压值。当负载电阻RL的值无限接近于无限大时，v表示压电片产生的开路电压。参数Cp表示压电片的电容量，Θ表示系统的电能转换系数，其值大小与压电片的压电常数d31呈正比。另外，式中非线性项可以表示为：

2 解析解求解

系统运动微分方程组(1)的解通常能使用MATLAB软件中的龙格库塔函数经数值计算得到。然而相对于解析解求解而言，数值计算过程需要经行多次冗长的迭代计算过程，同时数值计算得到的数值解底层数学模型不明显而不方便后续对该装置关键参数的优化研究。因此，本文将给出两自由度分段线性能量收集系统的解析解求解方法[19-20]。

(2)

式中引入的新参数可以表示为：

采用变换形式：

(3)

式中:引入的新参数Ak及θk分别表示系统分别处于一阶与二阶共振区间时所对应的幅值及相位角，相位角可以表示为θk=ωt+ϑk，ϑk表示初始相位角。可以观察到线性系统的解与非线性系统的解区别在于线性系统解中的幅值参数Ak及相位角参数ϑk为常数，而非线性系统中幅值参数Ak及相位角参数ϑk为相对于时间的变量。因此，对上文非线性系统的分析可以通过研究相位角与幅值的变化实现。

将假设解(3)代入方程组(2)中可以得到：

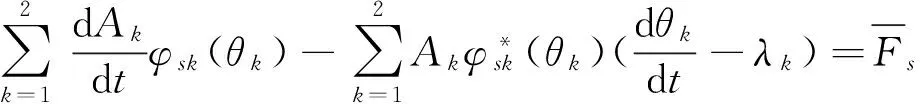
s=1,2,3,4,5

(4)

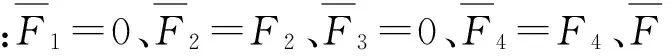
(5)

(6)

根据工程实际经验表明，当主梁在其两阶共振区间中的一个区间振动时，另外一个区间对应的主共振幅值对振动质量的位移的影响可以忽略不计。因此，当此处对主梁的第二阶共振区间进行讨论时，第一共振区间对应的幅值A1的值可以假设为0，非线性方程组(2)的近似解简化为Xs=A2φs2(θ2),s=1,2,3,4,5。由此，由等式(5)可求得参数φ2(A2,θ2)，经过简化，其表达式为：

(7)

为了求得参数φ2在一个完整周期的平均值，需要对非线性部分表达式f(A2,θ2)进行傅里叶变换。由于表达式f(A2,θ2)傅里叶变换式中的高阶谐波项相对于一阶谐波项而言，大小可忽略不计，保留一阶谐波项f(A2,θ2)的傅里叶表达式可表示为：

(k3cosθ2-λ2c3sinθ2)·H]

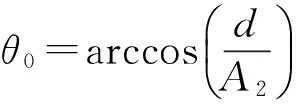
将参数φ2的表达式(7)代入平均值式(6)可得到：

新引入的参数δe(A2)表示幅值A2的等效衰减系数，其表达式为：

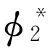
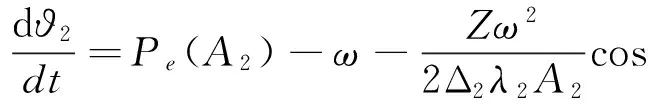
(9)

参数Pe(A2)表示系统等效线性固有频率，其表达式为：

(10)

(11)

由于主梁是在二阶共振区间内振动，式(10)中的参数2λ2可近似替换为2ω，同时式(11)中的参数2λ2可近似替换为Pe(A2)+ω。对方程组两边进行平方求和，可以得到幅值A2相对于激振频率ω的幅频响应关系表达式：

(12)

将式(12)中的参数λ2,A2,ϑ2,Δ2替换为参数λ1,A1,ϑ1,Δ1，可以得到第一共振区间对应幅值A1相对于激振频率ω的幅频响应关系表达式。

根据X5=v定义以及基础解系φ5k(θk)的值，可以求得电压幅值Vk表达式为：

(13)

由位移幅值Ak相对于激振频率ω的幅频关系表达式(12)及式(13)，可以快速求得电压幅值Vk相对于激振频率ω的幅频响应关系表达式。

3 样机加工与实验测试

3.1 实验样机加工

所提出新型能量收集装置的实验样机如图3所示，其主要参数见表1。装置的主梁与从动梁分别由铝片加工而成，主梁分为连续的两部分，第一段梁和第二段梁，在第一段梁上，贴有一片由Smart Material公司制造的型号为M-2814-P2压电纤维片作为电能转换部件。在每段梁的顶端，由螺栓组固定几片铝制质量片与各段梁一起作为等效振动质量。主梁与从动梁分别固定于基座的外部与内部部件上，基座内外两部件由螺栓组连接，内部部件可以上下移动以便调整振动质量m1与从动梁之间的间隙大小。

图3 实验样机Fig.3 The experimental prototype

参数数值第一段梁尺寸l1×b1×t1/mm340×20×0.5第二段梁尺寸l2×b2×t2/mm360×12×0.5从动梁尺寸l3×b3×t3/mm355×12×1.5等效振动质量m1/g9.6等效振动质量m2/g4.68间隙距离d/mm1等效电容Cp/nF25.7压电常数d31/(pm·V-1)170相对介电常数ε331560

3.2 实验测试方法

实验装置的连接简图如图4所示。实验样机固定于型号为JZK-5的电磁激振器上，激振器由型号为DH1301的信号发生器提供激振信号，由于DH1301信号发生器自带一个小型功率放大器，因此其产生的信号可直接驱动激振器工作。通过D1301信号发生器调节激振频率从15 Hz向60 Hz逐步增大进行扫频实验，在扫频过程中，基座上的加速度测量仪DH151可测量激振信号的加速度大小并通过动态信号分析仪DH5939D及PC端对其进行监控，通过反馈控制，保持激振信号的加速度大小在扫频过程中大小分别保持3 m/s2不变。压电片的输出电压由数字示波器DS5202CA测量，电信号通过外接10 MΩ的信号探针替代负载，可近似测量系统的开路输出电压值。

图4 实验装置图Fig.4 The entire experiment setup

4 结果与讨论

根据实验样机参数表1及实验测试方法中所给激振加速度值及外接负载值，可通过上文中给出的解析解结果表达式分别求得所加工样机在第一共振区间与第二共振区间的输出开路电压幅频曲线，同时，根据实验样机测试，也可得到实验样机的实验结果。

所提出新型能量收集装置及其对应线性系统第一共振区间的发电性能如图5所示。当外部激振频率由小往大变化时，实验值与理论值之间存在一定误差。由实验测得装置所对应线性系统的共振频率为19.3 Hz，与理论值得到的共振频率为21.2 Hz存在8.96%相对误差，这些误差可能是由实验中的测量误差和集中参模型中的一些模型简化造成的。同时可以观察到实验得到的线性系统开路电压小于理论计算值，分别为26.15 V和29.65 V，相对误差为11.8%，这种现象是因为压电片无法完美地贴附于悬臂梁上，从而导致压电片上的应力值及能量转换效率减小造成的。而观察分段线性系统开路电压实验值与理论值曲线可以发现，两者之间的差距明显大于线性系统，其在峰值处的值分别为22.35 V和26.86 V，相对误差达到了16.68%，这表明在分段线性系统中，除了由压电片不完美贴合造成的能量损失外，还有其他造成电压损失的因素。分析分段线性系统的运动特性，可知振动质量m1与从动梁之间的碰撞属于非完全弹性碰撞，正是由于非完全弹性碰撞中引起的能量损失造成系统电能转化效率的下降，但是所损失的能量并不会严重影响到系统的发电性能。

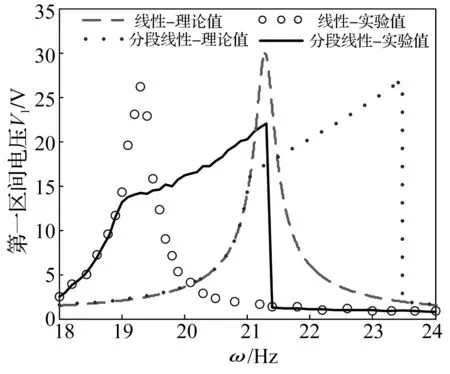
图5 第一共振区间电压幅频曲线Fig.5 The frequency response of the voltage in the first resonance region

虽然在共振频率点及峰值电压上，理论值与实验值存在一定的误差，但是所提出分段线性系统在第一共振区间上的电压幅频曲线变化趋势及工作频带拓宽性能上，所得到的实验值与理论值相吻合。从变化趋势看，电压幅频曲线首先沿着系统对应线性系统的电压幅频曲线变化，当外部激振频率增加到某一点位，分段线性系统中开始出现振动质量m1与从动梁之间的碰撞，其电压幅频曲线将改变原线性系统的幅频曲线变化趋势，呈缓慢上升变化，当外部激振频率持续增加到某一点位，由于非线性振动多解性导致的跳跃特性，电压幅频曲线将发生跳跃现象，电压幅值直接由高点位急剧下降至线性系统对应的值，之后再次沿着线性系统电压幅频曲线变化。从拓宽频带性能看，在第一共振区间内，分段线性系统在较高电压的工作频带宽度的实验值与理论值分别为2.2 Hz与2.4 Hz，相对于线性系统在对应电压值的工作频带宽度0.5 Hz而言，都有较大的拓宽比例。

所提出新型能量收集装置及其对应线性系统第二共振区间的发电性能如图6所示,对应线性系统在共振频率点与峰值电压的实验值与理论值都存在误差，造成误差的原因与第一共振区间类似。而观察分段线性系统的电压幅频变化曲线可发现，第二区间电压峰值的实验值与理论值之间的差距比第一区间要大，分别为14.01 V和18.51 V，相对误差达到了24.22%。这种现象同样是由振动质量m1与从动梁之间的碰撞损失造成的，系统在一阶共振区间工作时，工作频率大约为20 Hz，而在第二区间工作时，工作频率大约为50 Hz，这意味着系统在第二共振区间工作时发生碰撞的次数将大于第一共振区间，也将导致更多的碰撞能量损失，从而表现出系统在第二区间内的能量转换效率低于第一共振区间。考虑到此前一些线性结构的研究也存在10.2%左右误差的情况及文中模型对碰撞能量损失的忽略，文中所得相对误差在可接受范围之内。

系统在第二共振区间的变化趋势与第一区间类似，同时，系统在较高电压的工作频带宽度的实验值与理论值分别为4.5 Hz与4.6 Hz，相对于线性系统在对应电压值的工作频带宽度0.9 Hz而言，同样都有较大的拓宽比例。

图6 第二共振区间电压幅频曲线Fig.6 The frequency response of the voltage in the second resonance region

综合所提出分段线性系统在两区间的拓宽频带表现，其在较高电压处的总工作频带宽度的实验值为6.7 Hz，相对于对应的线性系统的工作频带宽度1.4 Hz而言，频带宽度拓宽了将近4.78倍。虽然，分段线性系统相对于线性系统电压峰值有所下降，但是针对环境中振源常在一定频率范围变化的实际情况而言，所提出装置能在较宽频率范围内保持比线性装置大得多的电压值(如图5中实验值对应的19.5 Hz到21 Hz及图6中实验值对应的48.4 Hz到51.6 Hz)，因此具有相对较高的能量收集效率。

5 结 论

为拓宽基于振动源的压电能量收集装置工作频带，提出一种新型两自由度分段线性能量收集结构，针对该结构提出理论模型并给出解析解结果，通过加工实验样机和搭建实验平台得到所提出新装置的能量收集性能，通过将实验值与理论值对比得到结论如下：

(1)虽然所给出的解析解理论值与实验值存在一定的误差，但误差值在可接受范围之内。与此同时，解析解所给出的电压幅频曲线变化趋势与频带拓宽性能与实验值保持一致，表明所提出理论模型与解析解结果可用于该装置进一步的参数优化设计与微小型化设计；

(2)不论是实验结果还是理论结果都表明所提出的两自由度分段线能量收集装置能够有效的拓宽工作频带拓宽，其工作频带总宽度能够达到6.7 Hz，与相对应的线性系统比较，频带拓宽效果能达到将近4.78倍。

[1] SAADON S, SIDEK O. A review of vibration-based MEMS piezoelectric energy harvesters [J]. Energy Conversion and Management, 2011, 52: 500-504.

[2] QURESHI E M, SHEN X, CHEN J J. Vibration control laws via shunted piezoelectric transducers: a review [J]. International Journal of Aeronautical and Space Sciences, 2014,15(1):1-19.

[3] QURESHI E M, SHEN X, CHEN J J. Piezoelectric shunt damping by synchronized switching on negative capacitance and adaptive voltage sources [J]. International Journal of Aeronautical and Space Sciences, 2014,15(4):396-411.

[4] QURESHI E M, SHEN X, CHANG L L. A low frequency vibration control by synchronized switching on negative capacitance and voltage sources [J]. International Journal of Control and Automation, 2015,8(6):121-138.

[5] 侯志伟,陈仁文,刘祥建, 多方向压电振动能量收集装置及其优化设计[J].振动与冲击，2012，31(16)：33-37. HOU Zhiwei，CHEN Renwen，LIU Xiangjian. Optimization design of multi-direction piezoelectric vibration energy harvester [J]. Journal of Vibration and Shock, 2012，31(16)：33-37.

[6] SOLIMAN M S M, ABDEL-RAHMAN E M, El-SAADANY E F, et al. A wideband vibration-based energy harvester [J]. Journal of Micromechanics and Microengineering, 2008, 18: 115021.

[7] LE C P, HALVORSEN E. MEMS electrostatic energy harvesters with end-stop effects [J]. Journal of Micromechanics and Microengineering, 2012, 22: 074013.

[8] LE C P, HALVORSEN E, YEATMAN E M, et al. Wideband excitation of an electrostatic vibration energy harvester with power-extracting end-stops [J]. Smart Materials and Structures, 2013, 22: 075020.

[9] HOFFMANN D, FOLKMER B, MANOLI Y. Fabrication, characterization and modelling of electrostatic micro-generators [J]. Journal of Micromechanics and Microengineering, 2009, 19: 094001.

[10] HOFFMANN D, FOLKMER B, MANOLI Y. Analysis and characterization of triangular electrode structures for electrostatic energy harvesting [J]. Journal of Micromechanics and Microengineering, 2011, 21: 104002.

[11] ZHOU W, PENAMALLI G R, ZUO L. An efficient vibration energy harvester with a multi-mode dynamic magnifier [J]. Smart Materials and Structures, 2012, 21: 015014.

[12] BLYSTAD L C J, HALVORSEN E. A piezoelectric energy harvester with a mechanical end stop on one side [J]. Microsystem Technologies, 2010, 17: 505-511.

[13] LIU H, LEE C, KOBAYASHI T, et al. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers [J]. Smart Materials and Structures, 2012, 21: 035005.

[14] LIU H, TAY C J, QUAN C, et al. A scrape-through piezoelectric MEMS energy harvester with frequency broadband and up-conversion behaviors [J]. Microsystem Technologies, 2011, 17: 1747-1754.

[15] GU L. Low-frequency piezoelectric energy harvesting prototype suitable for the MEMS implementation [J]. Microelectronics Journal, 2011, 42: 277-282.

[16] GU L, LIVERMORE C. Impact-driven, frequency up-converting coupled vibration energy harvesting device for low frequency operation [J]. Smart Materials and Structures, 2011, 20: 045004.

[17] HALIM M A, PARK J Y. Theoretical modeling and analysis of mechanical impact driven and frequency up-converted piezoelectric energy harvester for low-frequency and wide-bandwidth operation [J]. Sensors and Actuators A: Physical, 2014, 208: 56-65.

[18] DAQAQ M F, MASANA R, ERTURK A, et al. On the role of nonlinearities in vibratory energy harvesting: a critical review and discussion [J]. Applied Mechanics Reviews, 2014, 66: 040801.

[19] 陈予恕. 非线性振动[M]. 天津：天津科技出版社，1983.

[20] WEI S, HU H, HE S. Modeling and experimental investigation of an impact-driven piezoelectric energy harvester from human motion [J]. Smart Materials and Structures, 2013, 22: 105020.

Modeling and experiment of a piezoelectric energy harvester with wide operation bandwidth

LIU Shaogang, CHENG Qianju, ZHAO Dan, FENG Lifeng

(Mechanical & Electrical Engineering College, Harbin Engineering University, Harbin 150001, China)

A novel two-degree-of-freedom piecewise-linear piezoelectric energy harvester was proposed to achieve wide operation frequency bandwidth. The theoretical model was established and the analytical solutions were obtained for further optimized design and microminiaturization fabricating of the proposed device. Through the prototype fabricating and the experiment platform building, the experiment results were obtained. The analytical results and experiment results show that the operation frequency bandwidths of the proposed device in the first resonance region and in the second resonance region were 2.2 Hz and 4.5 Hz, respectively. The total bandwidth is 6.7 Hz, which reaches as 4.78 times as the corresponding linear system. Within the margin of error, the analytical solutions are close to the experiment results, and the proposed device can extend the bandwidth of the operation frequency efficiently.

piecewise-linear; two-degree-of-freedom; bandwidth extending; piezoelectric; energy harvester

国防技术基础科研基金资助项目(Z192013B001)

2015-09-23 修改稿收到日期：2015-11-23

刘少刚 男，博士, 教授，1962年生

TB123; TN384; O322

A

10.13465/j.cnki.jvs.2016.24.005