压电弹性梁主共振响应的时滞加速度反馈控制
2017-01-06谢献忠
彭 剑, 张 改, 胡 霞,谢献忠
(湖南科技大学 土木工程学院,湖南 湘潭 411201)
压电弹性梁主共振响应的时滞加速度反馈控制
彭 剑, 张 改, 胡 霞,谢献忠
(湖南科技大学 土木工程学院,湖南 湘潭 411201)
应用时滞加速度反馈控制方法研究压电弹性梁主共振响应的减振控制。基于Hamilton原理和时滞加速度闭环反馈控制策略,建立了压电耦合弹性梁的非线性动力学模型。采用多尺度方法,得到了受控梁主共振响应的一阶近似解及稳定性条件,进而给出了响应峰值和临界激励幅值的表达式,并给出算例分析。结果表明:采用时滞加速度反馈控制可以有效减振,其主共振响应受时滞值周期性影响,合理选取控制增益和时滞值,可以避免主共振区及多值不稳定解,提高振动控制效果。
压电弹性梁;主共振;时滞加速度反馈;振动控制;稳定性
端部非刚性支承弹性梁结构在工程领域极为常见,如斜拉桥主梁、大型体育场馆或厂房的横梁、地下结构桩基础等。大型复杂结构的重要性系数高,因此对其可靠性和稳定性及计算精度要求也越高。这类结构往往非线性的影响突出,振动与控制问题极为重要。
采用压电材料与结构复合而构成的主动控制系统是抑制梁结构大幅振动的有效方法,已有研究将其应用于工程结构的监测、抗振和自适应修复等[1]。同时,学者们从理论分析和实验方法对梁结构的非线性动力学及其振动控制进行研究[2-3]。值得一提的是,控制系统中的时滞影响及其时滞反馈控制得到了广泛关注。王在华等[4]从对当前时滞动力学研究进展作了系统的综述。冯志宏等[5]基于加速度时滞闭环反馈控制策略,研究了压电耦合悬臂梁的时滞反馈控制及稳定性。陈龙祥等[6]对旋转运动柔性梁的时滞主动控制开展了实验研究,得到控制系统中的时滞也有可利用的价值。赵艳影等[7]研究了时滞非线性动力吸振器的减振机理,通过调节反馈增益系数和时滞来实现主系统的减振。李欣业等[8]研究了陀螺系统的受迫振动及时滞反馈控制。尚慧琳等[9]对一类转动系统的复杂运动开展了时滞速度反馈控制研究。DAQAQ等[10]采用时滞加速度反馈控制研究了压电耦合悬臂梁的非线性振动。MASOUD等[11-12]针对起重机大幅振动问题,采用状态时滞反馈策略对其进行控制,起到了很好的抑制效果。孙清等[13]研究了含双时滞振动主动控制系统超谐共振及亚谐共振。
本文以轴力作用下的耦合弹性梁结构为研究对象,推导出压电耦合弹性梁的非线性动力学方程,并结合压电传感器与作动器的输出方程,建立了压电耦合弹性梁的动力学模型。同时基于时滞加速度反馈控制技术,研究了系统主共振响应的减振控制。
1 振动控制方程
轴力作用下弹性支座梁与压电作动器和传感器共同构成闭环反馈控制系统如图1所示,其中悬臂梁为Euler-Bernoulli梁,梁不可伸长且忽略其扭转和剪切变形,假设压电材料理想地埋入梁内,不考虑压电材料的质量及刚度影响。
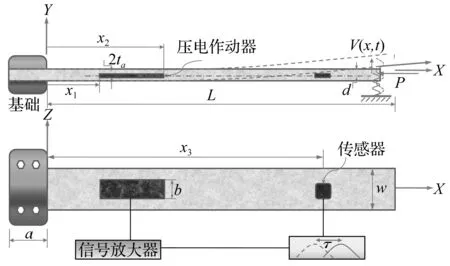
图1 时滞反馈激励梁控制系统结构图Fig.1A schematic of a beam with delayed feedback actuation
基于Hamilton原理,考虑轴力弹性支座和压电激励作用,得到受控梁的非线性动力学方程[14-15]:
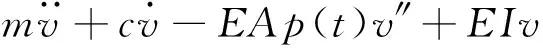
(1)
边界条件为:
v(0,t)=0,v′(0,t)=0,v″(l,t)=0,
EIv‴(l,t)+kv(l,t)=0
(2)
式中:m,c分别为梁的线密度、阻尼,E为梁的弹性模量,p为轴向作用力,k为弹性刚度系数,I为截面惯性矩,l为梁的长度。q(x,t)=∂2M/∂x2是由压电作动器产生的分布荷载,M为压电材料产生的应力生成关于整个结构中性轴的力矩,其表达式为:
[H(x-x1)-H(x-x2)]
其中,b为压电材料宽度,d为压电材料中截面距梁结构中截面距离,d31为压电材料的电荷压电常数,Ea为压电材料的弹性模量,Va(t)为外加控制电压,2ta为压电作动器的厚度,x1,x2分别为作动器固定在梁上的位置坐标。
运用Galerkin方法对其位移函数v(x,t)进行展开:
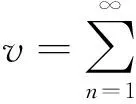
(3)
式中:φn(x)为振型函数,表达式表示为,
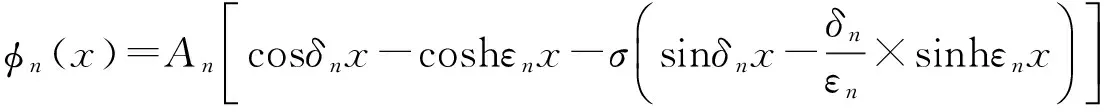
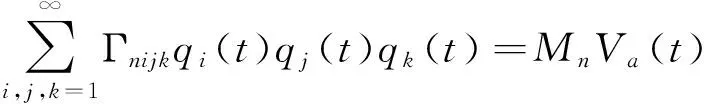
n=1,2,…,∞
(4)
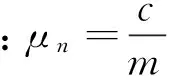
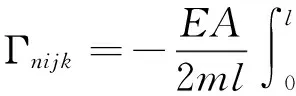
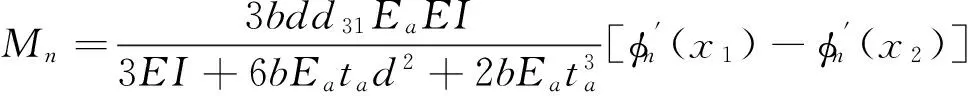
(5)
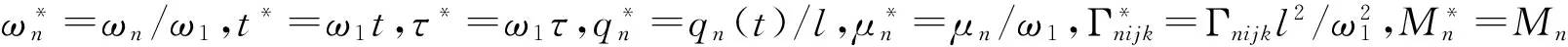
本文考虑压电激励的驱动电压采用加速度时滞反馈策略,记为如下形式:
(6)
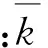
(7)
则受迫振动下单模态梁的响应方程为:
(8)
式中:fn为外激励幅值,Ω为外激励频率。
2 主共振响应分析
本节采用多尺度法求解单模态梁的主共振解,调整阻尼,非线性及外激励项的系数:
μn=Ο(ε),Γnnnn=Ο(ε),kann=Ο(ε),
fn=Ο(ε),Ω=ω0+εσ,σ=Ο(1)
(9)
2.1 主共振近似解析解
设式(8)的摄动解形式为:
qn(t)=qn0(T0,T1)+εqn1(T0,T1)+…,
Tj=εjt,j=0,1
(10)
将式(10)代入式(8),令两端的ε0和ε1的系数相等,得到:
(11)
fncos(ω0T0+σT1)
(12)
式(11)的通解可以写为:
qn0=An(T1)exp(iω0T0)+
(13)
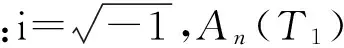
(14)
式中:cc代表前面各项的共轭复数。消去式(14)中的久期项,可得:
(15)
令:
(16)
式中:an和βn是T1的实函数。分离实虚部,得到:
(17)
式中:γn=σT1-βn。则可得压电弹性梁主共振的幅频响应方程:
(18)
相应地,压电弹性梁位移v(x,t)的一阶近似解为:
v(x,t)=ancos(Ωt-γn)φn(x)+Ο(ε)
(19)
同时,根据幅频响应方程式(18)可得主共振最大幅值的表达式:
(20)
进一步,可得到:
(21)
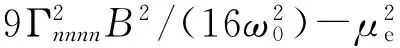
fL=2ω0μe(2ω0μe/3Γnnnn)1/2
(22)
2.2 周期解的稳定性
本小节主要通过式(17)来确定周期解的稳定性,设:
an=an0+an1,γn=γn0+γn1
(23)
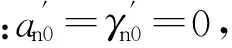
其特征方程为:
(25)
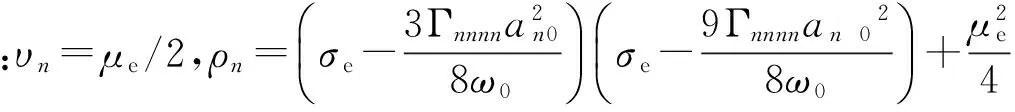
周期解的稳定性依赖于式(21)特征方程的特征值,因此根据稳定性理论有:当υn>0,ρn>0时周期解稳定,反之不稳定。
3 数值分析与讨论
本节对受控梁第一阶模态的主共振响应进行数值分析,讨论其与控制增益和时滞量之间的关系。梁和压电激励器的几何尺寸和材料特性参数如下。梁:l=99.62×10-2m,A=15.36×10-4m2,E=34.5 GPa,I=9.866 2×10-8m4,k=6.872×104N/m,p=2.574×10-1kN,m=4.4 kg/m;压电激励器:d31=-270×10-12m/V,Ea=108 GPa,b=0.2×10-2m,2ta=0.04×10-2m,d=0.5×10-2m,x1=12×10-2m,x2=18×10-2m,x3=80×10-2m。
给定f1=0.005,μ1=0.02,图2为控制增益k=-2时时滞影响下压电耦合弹性梁第一阶模态主共振响应的幅频曲线。从中可以看出,当τ=π/4时,其响应幅值较τ=π/30显著减小,然而当τ=π时,幅值急剧增大,当τ=5π/4时,幅值又得到抑制,且曲线有多值区域,共振区发生偏移。
值得提出的是,图3给出的响应幅值峰值曲线恰好证明了这一点,当时滞τ∈(kπ,kπ+π/2),k=0,1,…时,幅值随时滞t增大而减小,而当时滞值τ∈(kπ+π/2,kπ+π)时,响应幅值随时滞增大而增大,且幅值的变化率在一段区间内显著高于时滞值变化率。
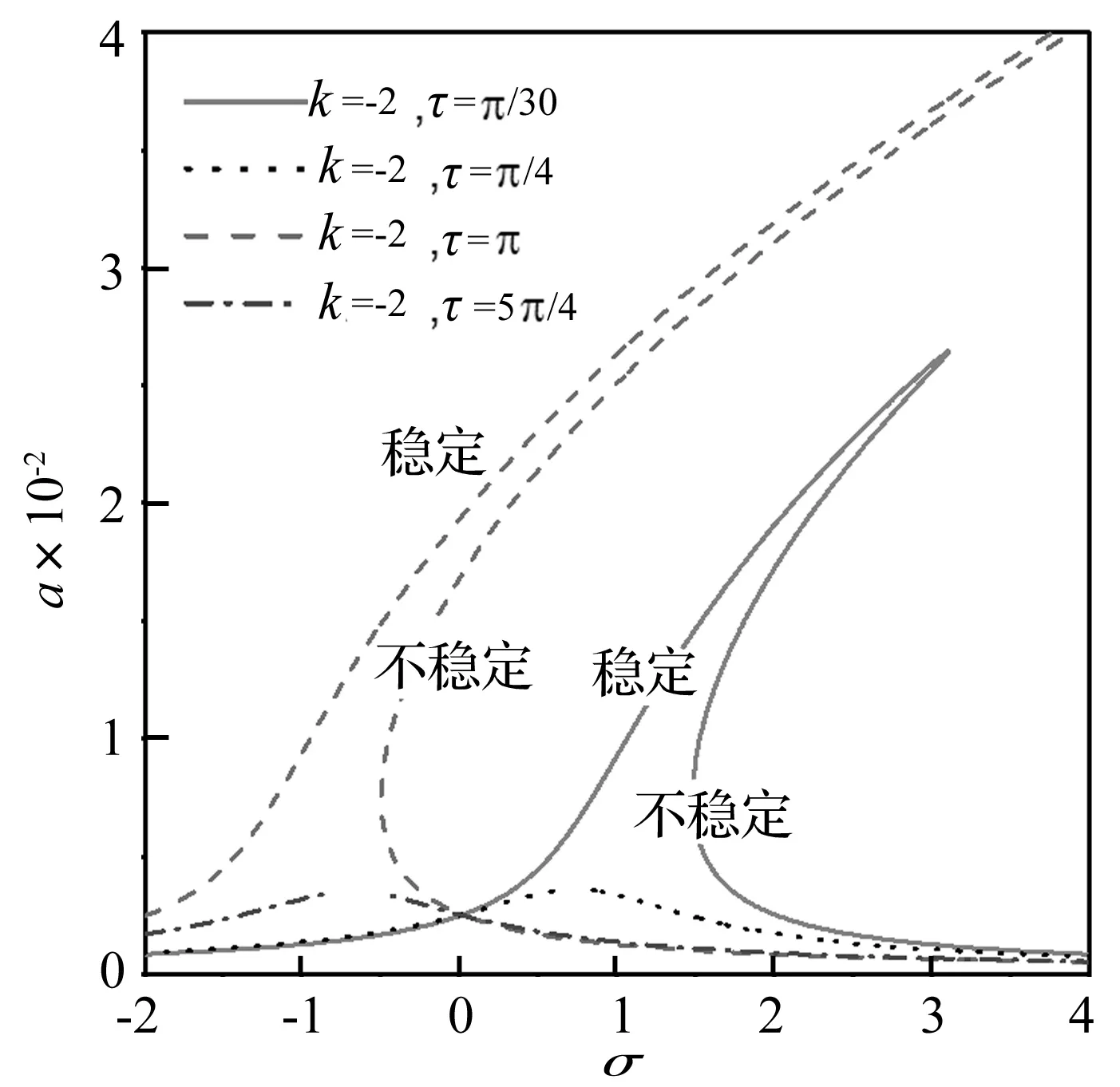
图2 不同时滞值时受控梁第一模态主共振响应幅频曲线Fig.2 The amplitude-frequency curves of the first mode (n=1) primary resonance response of beam with time delay
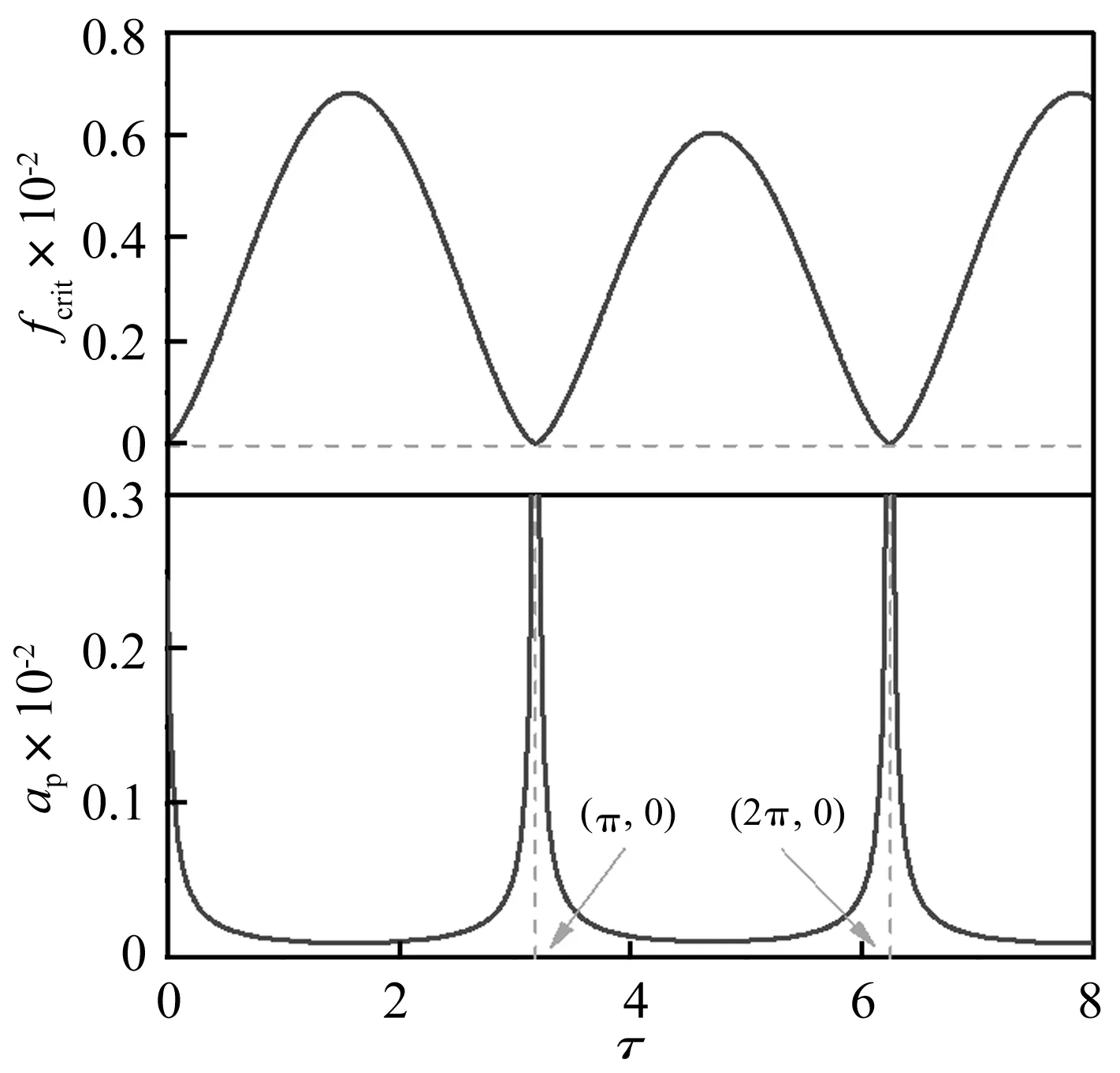
图3 不同时滞值时受控梁第一模态主共振临界激励和响应峰值曲线Fig.3 The curves of the critical excitation and the peak amplitude of the primary resonance response of beam with time delay
图3中同时给出了临界激励值曲线。该曲线与幅值峰值曲线均呈现出周期性,此处周期T=2π。给定控制增益和时滞值,当外激励幅值fn
图4为当时滞τ=π/30时,不同控制增益影响下,压电耦合梁第一模态主共振响应幅频曲线。可以看出,当k=0,即无控状态下,幅值较大。当采取时滞加速度反馈控制后,幅值得到明显抑制,且控制效果与k值正相关。同时可以发现,随着k值的不同,共振区发生明显偏移。
图5给出了不同时滞τ和调谐参数σ情况下系统第一模态的激励-响应幅值曲线。从中可以看出,随着σ值的增大,曲线实现了从单值到多值的转换,且出现不稳定解,同时响应幅值增大,弯曲程度增强。固定相应σ值,随着时滞τ增大,也显示出相同的现象。因此,在共振范围内,非线性特征随着时滞值和调谐参数的增大表现更为明显。
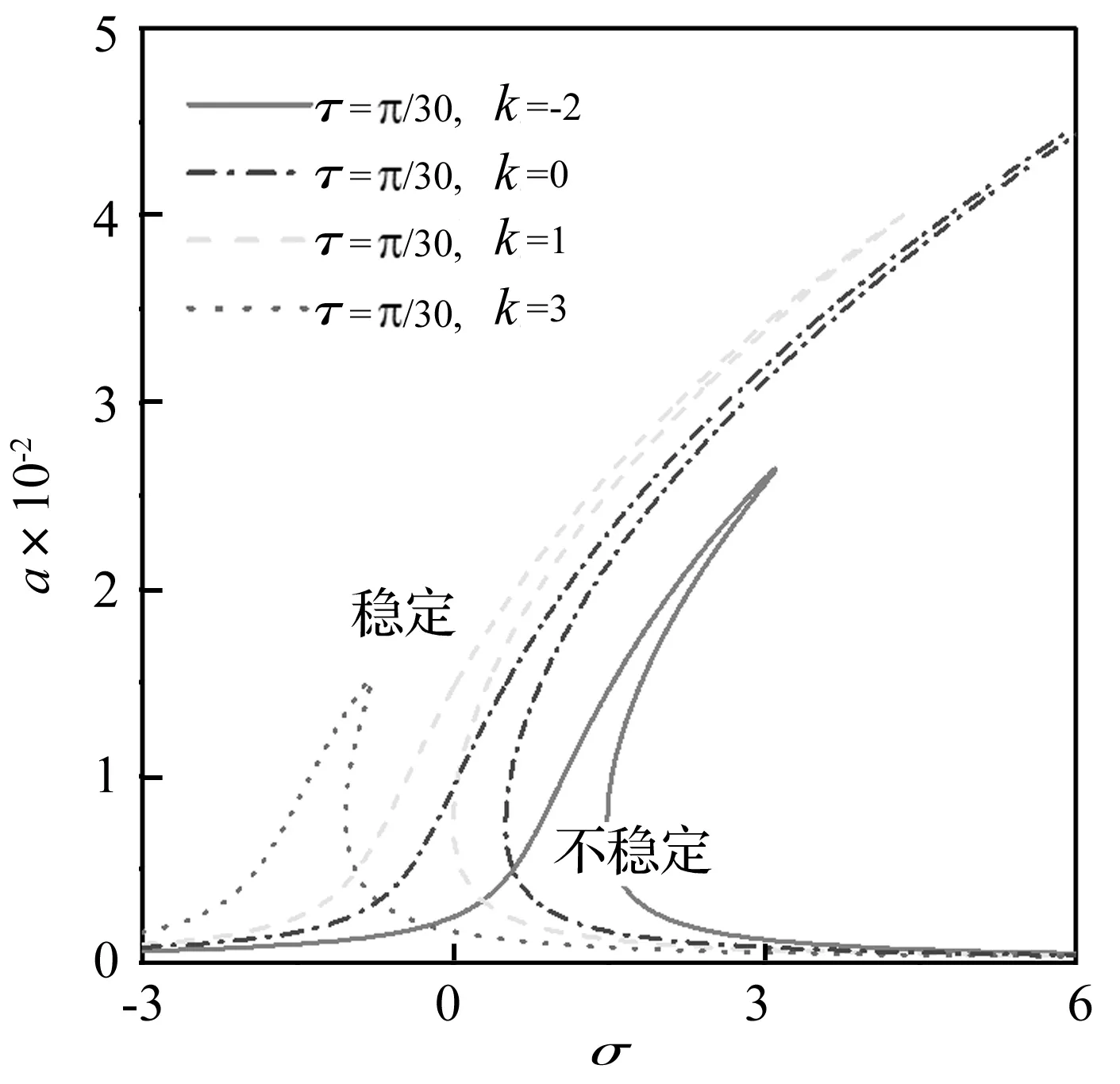
图4 不同控制增益值时受控梁第一模态主共振响应幅频曲线Fig.4 The amplitude-frequency curves of the first mode primary resonance response of beam with control feedback gain
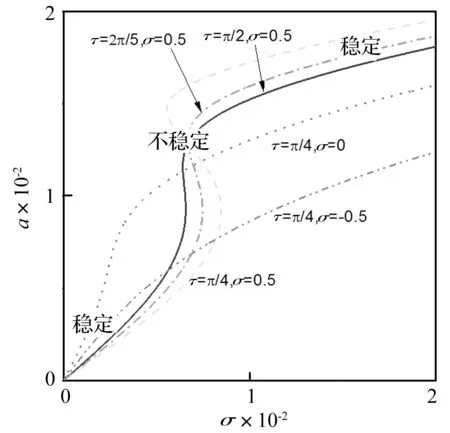
图5 时滞作用下主共振响应激励-响应幅值曲线Fig.5 The response-excitation amplitude curve of the primary resonance with time delay
图6给出的发生主共振和非主共振硬激励时,压电耦合梁稳态运动时的振动响应时程曲线对比图。对比图中三条曲线响应幅值,可知发生主共振时系统的响应幅值显著增大,且控制增益k=0.5时,幅值明显大于小时滞情形。因此,时滞值对系统实际动力影响很大,且必须考虑主共振作用。
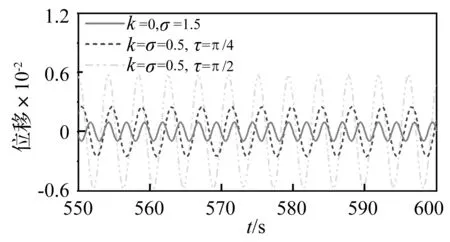
图6 时程曲线对比Fig.6 The contrast of time history curves
图7为无控和受控情形下发生主共振的频域分析图,可以看出,发生主共振的时的稳态频率没有太大差别,但是其位移幅值有显著变化,采用时滞反馈控制后,其幅值得到了明显抑制。
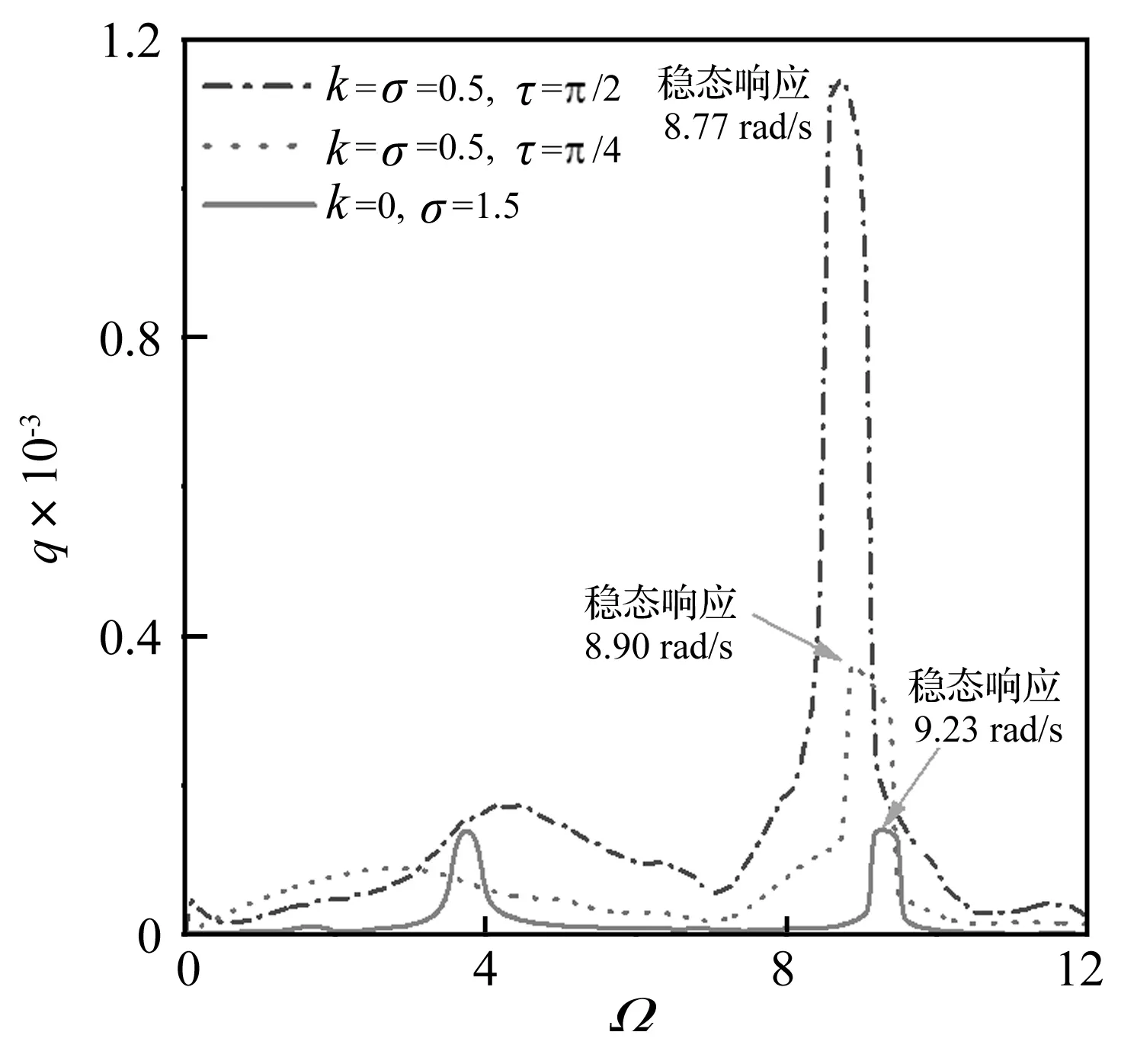
图7 不同时程曲线的FFT变换Fig.7 The Fast Fourier Transformation of time history curves
4 结 论
本文研究了压电耦合弹性梁主共振的时滞反馈控制,采用时滞加速度反馈控制策略,运动多尺度方程得到主共振响应的解析解。通过数值算例,得出结果如下:
(1)采用时滞加速度反馈控制,可以有效抑制其大幅振动,其主共振响应受时滞值周期性影响;
(2)调整控制增益和时滞值,可以避免主共振区及多值不稳定解;
(3)主共振硬激励幅值明显低于主共振幅值,因此研究主共振响应的控制具有工程实际意义。
[1] 欧进萍. 结构振动控制——主动、半主动和智能控制[M]. 北京:科学出版社,2003.
[2] HIROSHI Y, SHIGENOBU S, NOBUHARU A. Stabilization of the parametric resonance of a cantilever beam by bifurcation control with a piezoelectric actuator[J]. Nonlinear Dynamics, 2001, 26(2): 143-161.
[3] 朱辰钟,叶敏. 参强联合作用非线性结构动力学实验建模[J]. 力学学报, 2013,45(1): 116-128. ZHU Chenzhong, YE Min. Research of dynamic experimental modeling for nonlinear structure under parametric and forced excitation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013,45(1): 116-128.
[4] 王在华,胡海岩. 时滞动力系统的稳定性与分岔:从理论走向应用[J]. 力学进展, 2013, 43(1):1-20. WANG Zaihua, HU Haiyan. Stability and bifurcation of delayed dynamics systems: From theory to application[J].Advances in Mechanics,2013, 43(1):1-20.
[5] 冯志宏, 霍睿. 压电耦合悬臂梁的时滞反馈控制及稳定性分析[J]. 振动与冲击, 2011, 30(6): 181-184. FENG Zhihong, HUO Rui. Time-delay feedback control and stability analysis of piezoelectric-coupling cantilever beam[J]. Journal of Vibration and Shock, 2011, 30(6): 181-184.
[6] 陈龙祥,蔡国平. 旋转运动柔性梁的时滞主动控制实验研究[J]. 力学学报, 2008, 40(10): 520-527. CHEN Longxiang, CAI Guoping. Experimental study on active control of a rotating flexible beam with time delay [J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(10): 520-527.
[7] 赵艳影, 徐鉴. 时滞非线性动力吸振器的减振机理[J].力学学报, 2008,40(1):98-105. ZHAO Yanying, XU Jian. Mechanism analysis of delayed nonlinear vibration absorber[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008,40(1):98-105.
[8] 李欣业, 张利娟, 张华彪. 陀螺系统的受迫振动及其时滞反馈控制[J].振动与冲击, 2012, 31(9): 63-68. LI Xinye, ZHANG Lijuan, ZHANG Huabiao. Forced vibration of a gyroscope system and its delayed feedback control[J]. Journal of Vibration and Shock, 2012, 31(9): 63-68.
[9] 尚慧琳,李伟阳,韩元波. 一类相对转动系统的复杂运动及时滞速度反馈控制[J]. 振动与冲击, 2015, 34(12): 127-132. SHANG Huilin, LI Weiyang, HAN Yuanbo. The complex dynamics of a relative rotation system and its control by delay velocity feedback[J]. Journal of Vibration and Shock, 2015, 34(12): 127-132.
[10] DAQAQ M F, ALHAZZA K A, ARAFAT H N. Non-linear vibrations of cantilever beams with feedback delays [J]. International Journal of Non-linear Mechanics, 2008, 43: 962-978.
[11] MASOUD Z, DAQAQ M F, NAYFEH N H. Pendulation reduction of small telescopic cranes[J]. Journal of Vibration and Control, 2004, 10(8): 1167-1179.
[12] MASOUD Z, NAYFEH A H, AL-MOUSA A. Delayed-position feedback controller for the reduction of payload pendulations on rotary cranes [J]. Journal of Vibration and Control, 2003, 9(1/2): 257-277.
[13] 孙清,张斌,刘正伟,等. 含双时滞振动主动控制系统超谐共振及亚谐共振分析[J]. 工程力学, 2010, 27(12): 84-89. SUN Qing, ZHANG Bin, LIU Zhengwei, et al. Analysis of superharmonic and subharmonic resonance responses of active vibration control system with double time delay [J]. Engineering Mechanics, 2010, 27(12): 84-89.
[14] NAYFEH A H. Linear and nonlinear structure mechanics [M]. New York: Wiley Interscience, 2004.
[15] 彭剑, 赵珧冰, 王连华. 时滞反馈及轴力作用下弹性梁的非线性振动[J]. 湖南大学学报(自然科学版), 2013, 40(9):30-36. PENG Jian, ZHAO Yaobing, WANG Lianhua. Nonlinear vibrations of elastic beams subjected to axial force and delayed-feedback[J]. Journal of Hunan University (Naturnal Science), 2013, 40(9):30-36.
Time-delayed acceleration feedback control of primary resonance of piezoelectric elastic beams
PENG Jian, ZHANG Gai, HU Xia, XIE Xianzhong
(School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)
The time-delayed acceleration feedback control method was applied to study the primary resonance response of vibration control of piezoelectric flexible beams. Based on the Hamilton principle and a closed-loop feedback control strategy with delayed acceleration, a piezoelectric coupling nonlinear dynamic model of the elastic beam were established. Utilizing the multiple scale method, the first-order approximate solution and the stability condition of the primary resonance response of controlled beam were obtained. The peak amplitude and the critical excitation amplitude were given. It is shown that using time-delayed acceleration feedback control can reduce vibration effectively, and that the primary resonance response is affected by the delay value periodically. Reasonable selection of control gain and time delay value can avoid the resonance region and improve the effect of vibration control.
piezoelectric elastic beam; primary resonance; time-delayed acceleration feedback; vibration control; stability
国家重点基础研究发展计划(973)项目(2015CB057702);国家自然科学基金项目(11402085;11272119);湖南省教育厅项目(14C0464); 湖南省优秀博士论文资助项目(YB2015B035)
2015-11-26 修改稿收到日期:2016-01-25
彭剑 男,博士,硕士生导师,1982年11月生
O328; TB123
A
10.13465/j.cnki.jvs.2016.24.001
