基于ITD复杂度和PSO-SVM的滚动轴承故障诊断

张小龙， 张 氢， 秦仙蓉， 孙远韬

(同济大学 机械与能源工程学院，上海 201804)

基于ITD复杂度和PSO-SVM的滚动轴承故障诊断

张小龙， 张 氢， 秦仙蓉， 孙远韬

(同济大学 机械与能源工程学院，上海 201804)

针对滚动轴承故障诊断问题，提出了一种基于固有时间尺度分解(ITD)、Lempel-Ziv复杂度特征和粒子群优化支持向量机(PSO-SVM)的故障诊断新方法。首先对滚动轴承的振动信号使用ITD方法进行分解，得到若干个频率由高到低的固有旋转(PR)分量，由于滚动轴承在不同的故障状态下的PR分量Lempel-Ziv复杂度的分布不同，提取各PR分量的Lempel-Ziv复杂度值作为每个样本的特征向量，使用支持向量机(SVM)对轴承振动信号样本进行故障类型的识别，并用粒子群优化(PSO)方法对支持向量机的参数优化以获得较高的识别准确率。对滚动轴承振动信号的实测结果的分析表明：该方法可以实现对滚动轴承快速、准确地诊断，且不受载荷变化的影响。

固有时间尺度分解；Lempel-Ziv复杂度；支持向量机；粒子群优化；滚动轴承；故障诊断

滚动轴承是旋转类机械设备中广泛使用的传动部件之一，运行时发生故障可能会引起整个传动系统的失效，因此对其进行故障诊断的研究具有重要意义。振动分析是机械设备故障诊断的主要方法之一，基于振动信号的故障诊断方法主要分为信号预处理、特征提取、状态识别三个步骤[1]。

滚动轴承振动信号一般具有非平稳、非线性的特点，对原始信号直接提取特征值来实现故障诊断是比较困难的。对信号分解是预处理常用的手段，常用的分解方法有小波分解(WD)、经验模态分解(EMD)、集合经验模态分解(EEMD)、局域均值分解(LMD)等方法[2]。固有时间尺度分解(Intrinsic Time Scale Decomposition， ITD)方法能够将任何复杂信号分解为若干个相互独立的瞬时频率具有物理意义的固有旋转(Proper Rotation，PR)分量之和，在端点效应和计算速度等方面优于EMD方法和LMD方法，适于实时在线的数据处理[3-4]。

在特征信号提取方面，基于非线性动力学参数如模糊熵、近似熵、样本熵等广泛用于机械故障特征信号的提取[3, 5-6]，但当待处理的数据量较大时，对这些非线性动力学参数的计算需要耗费较长的时间。复杂度指标反映的是给定有限序列随其长度增长而出现新模式的速率，是衡量有限时间序列复杂程度的高效工具，Lempel-Ziv提出的复杂度算法计算效率高，且复杂度值对系统的状态变化敏感。正常状态的滚动轴承运行时振动信号的波动周期性强，信号规律较为简单和有序，因此复杂度较低，但是当轴承出现故障时，故障会使轴承的振动信号产生冲击，使得振动信号规律变得复杂和无序，因此其复杂度会改变并升高。因此可以将Lempel-Ziv复杂度指标引入到滚动轴承故障诊断[7-8]，计算在不同的运行状态下的Lempel-Ziv复杂度值，用于构建滚动轴承振动信号的特征向量。

支持向量机(Support Vector Machine，SVM)算法能够较好地解决小样本、非线性、局部极小等问题，进行有效分类，广泛用于机械设备状态识别。支持向量机分类中，核函数参数和惩罚因子的选择会对分类效果产生较大影响[9]。粒子群优化(Particle Swarm Optimization，PSO)算法是一种基于群智能的全局寻优方法，具有计算简单、收敛速度快、全局和局部都有良好的收敛能力等优点[10]。将PSO算法用于SVM参数的优化中，可以改善根据经验选择核函数参数和惩罚因子所导致的SVM分类识别率低的缺点。

本文将ITD方法应用于滚动轴承振动信号的分解预处理，提取ITD分解后PR分量的Lempel-Ziv复杂度构建特征向量，将其输入到SVM中，通过PSO算法优化SVM参数以构建最优的SVM分类器，实现对滚动轴承不同类型故障的准确识别。

1 固有时间尺度分解(ITD)

设Xt为待分解的实值离散信号，定义L为基线提取算子，Lt为基线分量，Ht为固有旋转量。为简化符号，定义Xk表示X(tk)，Lk表示L(tk)。ITD步骤如下[3-4]：

(1)提取Xt序列的极值点Xk和对应时间{τk,k=1,2,…,N}，并定义τ0=0。

在区间(τk，τk+2]上定义一个分段线性基线提取算子L：

(1)

式中，t∈(τk,τk+1]。

定义：

(1-α)Xk+1

(2)

式中，α用于控制提取固有旋转分量幅度的线性缩放，α∈[0,1]，通常取α=0.5[4]。

(2)利用步骤(1)中计算出的基线信号Lt=LXt，按照式(3)提取出固有旋转分量Ht：

Xt=LXt+(1-L)Xt=Lt+Ht

(3)

Ht=(1-L)Xt即为固有旋转分量。

(3)将基线信号Lt作为下一次分解的输入信号重复(1)、(2)步骤，多次分解后，直到获得基线信号Lt变得单调或者小于某个预定值为止。

经过ITD算法后将原信号Xt分解为多个从高到低不同频率段的固有旋转分量和一个单调趋势分量之和。

2 Lempel-Ziv复杂度计算

Lempel-Ziv复杂度算法是由Lempel和Ziv提出的一种度量符号序列的复杂度的算法，在计算信号的复杂度之前，需先对信号进行“粗粒化”处理，目前使用较多的是二值粗粒化，对信号序列求出平均值，对序列中对于大于平均值的点赋值1，小于平均值的点赋值0，这样得到一串1、0组成的序列。对原始数值序列Xt的复杂度计算步骤如图1所示，对于原始数值序列Xt二值化后得到符号序列S(s1,s2,…,sN)。首先将临时字符变量P0、Q0初始化为空字符，令i=0，复杂度C(i)=0。然后开始N次循环，计算复杂度CN值，每次循环时，令Pi={Pi-1si}，Qi={Qi-1si}分别表示由Pi、Qi与si连接而成的字符串，判断Qi是否为Pi-1的子字符串，若是则表示当前没有出现新模式，复杂度C(i)值不变，否则表示出现了新模式，复杂度C(i)值加1，这样循环N次后可以遍历判断Xt所有的值，计算出序列的复杂度CN，对CN归一化得到归一化复杂度C。

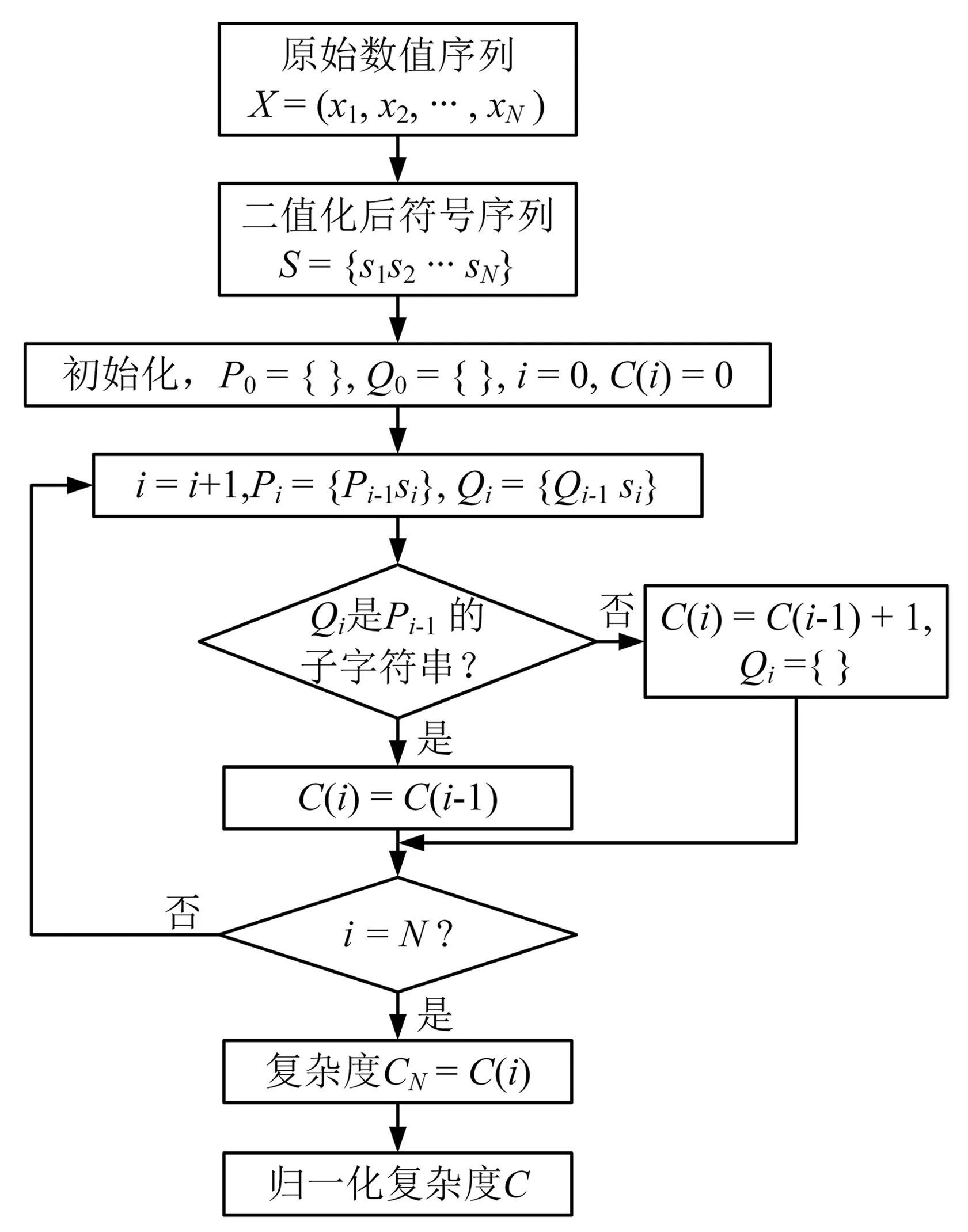
图1 Lempel-Ziv复杂度算法流程图Fig.1 Flowchart of Lempel-Ziv complexity algorithm

Lempel和Ziv已证明，当N→∞时，CN会趋近于定值N/loglN，其中l为粗粒化的段数，二值粗粒化时l=2，归一化的Lempel-Ziv复杂度为

(4)

3 基于粒子群优化的支持向量机故障诊断

3.1 支持向量机

Vapnik等提出的支持向量机(SVM)算法为基于结构风险最小化方法的统计学习理论，具有很强的学习能力和泛化能力，能够较好地解决小样本、非线性、局部极小等问题，实现有效分类。

SVM对于线性不可分问题，通过引入核映射方法转化为高维空间的线性可分问题来实现分类。核函数的选择是SVM方法的关键，常用的核函数有径向基函数(RBF)、多项式核函数、Sigmoid核函数[10-11]。RBF核函数在实际应用中取得了较好的效果，且RBF核函数使用时只需要确定一个核函数参数σ，本文使用SVM分类方法时选用RBF核函数。此外，惩罚参数C也会对分类的性能产生较大影响，因此，有必要引入寻找最优的σ、C的方法，以获得较高的分类精度。

SVM多分类问题主要“一对多”、“一对一”、“二叉树”等方法，“一对一”是在任意两种类别之间设计一个分类器，通过“投票法”算法来确定待分样本最终归属的类别[12]。其优点是识别和训练的速度会比较快，缺点则是在遇到类别较多的问题时需要构造的分类器也较多。考虑到轴承常见的故障类型有限，本文采用“一对一”的方法进行SVM多分类。

3.2 粒子群优化算法

粒子群优化(PSO)算法是一种基于群智能的全局寻优方法，它通过个体间的协作与竞争来实现复杂解空间中最优解的搜索，很适合用于SVM参数的选择和优化。

粒子群算法求解时，首先在解空间中初始化一群粒子，每个粒子都表示优化问题的一个潜在解，用位置、速度和适应度值刻画其特征，适应度值则由适应度函数来确定，以确定粒子的优劣。在粒子群寻优过程中，每个粒子通过迭代法都在解空间全局搜索。在每次迭代中，都会产生所有粒子的全局最优解和粒子自身的当前的最优解，每个粒子会按照式(5)和(6)更新速度和位置，逐代搜索，直到得到最优解。

vid(t+1)=ωvid(t)+c1r1(pid(t)-xid(t))+

c2r2(pgd(t)-xid(t))

(5)

xid(t+1)=xid(t)+vid(t+1)

(6)

式(5)、(6)中，d=1,2,…,n是种群维数，即求解问题在n维空间中；i表示所有的粒子中的第i个粒子；t是当前迭代数；ω为惯性权重；c1和c2是加速常数或学习因子；r1和r2是(0, 1)之间均匀分布的随机数；vid∈[-vmax,vmax]为粒子的飞行速度，vmax表示粒子最大飞行速度，代表粒子在解空间的搜索能力；xid代表粒子在当前搜索空间的位置；pid表示粒子自身迄今为止搜索到的最优位置；pgd表示整个粒子群迄今为止搜索到的最优位置。

PSO算法优化SVM时，以核函数参数σ和惩罚参数C为待优化参数，优化目标是获得最高的分类准确率。使用PSO算法优化SVM时首先对粒子群规模、群维数、限制速度、加速常数、初始速度和位置等进行初始化；使用每个粒子位置向量构建SVM对训练样本进行预测，把各个粒子当前位置识别误差作为其适应度值，比较各粒子自身最优位置适应度值与群体最优位置适应度值，如果前者较优，则将该粒子最优位置作为群体的最优位置；更新粒子的位置及速度；检查结束条件，若不满足则按式(5)、(6)继续迭代计算，直到满足条件并输出结果[12]。

3.3 基于PSO-SVM的故障诊断步骤

如图2所示为基于PSO-SVM的故障诊断流程图。对滚动轴承正常和常见的故障类型信号进行采集，得到原始的振动信号。使用ITD方法对每个振动信号样本进行分解，得到前m个PR分量，计算每个PR分量的复杂度，则对于每个信号样本可以构建出其m维特征向量空间。将采集到的振动信号分为训练样本集和测试样本集，将训练样本集的特征向量和其状态类别号输入到训练SVM中，通过PSO算法优化训练SVM参数，以获得最小的分类误差，得到训练好的SVM。将测试样本集输入到训练好的SVM中，训练好的SVM能识别出其所属的状态类别，从而实现不同故障的诊断。

图2 基于粒子群优化支持向量机的滚动轴承故障诊断流程图Fig.2 Flowchart of rolling bearing fault diagnosis based on PSO-SVM

4 滚动轴承故障诊断实例分析

为研究本文提出的滚动轴承故障诊断方法的有效性，选用了美国凯斯西储大学电气工程实验室的轴承实验数据。实验时使用电火花单点对轴承进行不同程度的损伤，制造轴承内圈、外圈及滚动体故障，故障深度均为0.279 mm，故障直径大小为0.178 mm。通过调节负载，使轴承分别在0 kW、0.735 kW、1.470 kW、2.205 kW的负载功率下运转，不同负载下的轴承转速略有不同，但均约在30 Hz。将加速度传感器安装在电机的驱动端的轴承座来获得轴承的振动信号，采样频率为12 kHz。

每种载荷和运行状态的数据总长度为12 000点，将其按每1 200点分割作为一个样本，每种载荷和状态类型下得到100组数据样本(共400组)。对每个样本用ITD方法分解，得到各个样本的PR分量，并对载荷为0 kW时四种状态下的各一组样本进行EMD、EEMD分解计算。在进行EEMD分解时使用了文献[13]推荐的算法执行EMD的总次数M=100，信号中添加的白噪声序列幅值系数k=0.1。对比EMD、EEMD、ITD分解计算时间如表1所示。由表1可知，对同一信号分解时，ITD方法使用的时间明显少于EMD和EEMD方法。这是因为ITD算法不像EMD算法采用样条插值，ITD每分解一次就获得一个PR分量，每次分解只需要迭代一次，而EMD算法每获得一个IMF分量需要经过多次迭代[14]。而EEMD方法的核心也是EMD，在计算时需要对添加噪声后的信号进行多次EMD计算，所以使用时间会比EMD还要多。因此，从分解效率上来对比，ITD方法更适合在线分析。

表1 各种状态EMD、EEMD和ITD计算时间对比Tab.1 The time consumption comparison among EMD, EEMD and ITD under different conditions

如图3所示,载荷为0 kW时内圈故障轴承振动信号时域图和ITD方法分解后前5个PR分量的时域图，由图3可以看出，轴承振动信号的能量主要集中在前几个高频段PR分量，将PR1、PR2、PR3重构后得到的信号与原信号的相关度达到了0.997，因此前3个PR分量已经可以描述振动信号的特征信息。用前3个PR分量的Lempel-Ziv复杂度值构建每个样本的特征向量，表2所示为不同载荷下正常和三种故障状态时滚动轴承振动信号特征向量值，表中“样本1”和“样本2”为从相应载荷和状态下随机选出的两个样本，“均值”为相应载荷和状态下的100个样本的特征向量值的平均值。由表2可以得出以下结论：

(1)相同载荷时，不同状态的同一PR分量的复杂度的值差别较大，这说明PR复杂度作为特征向量具备类间离散度大的特点；

(2)相同载荷时，同一状态的样本PR分量复杂度较为接近，这说明PR分量复杂度作为特征向量具备类内离散度小的特点；

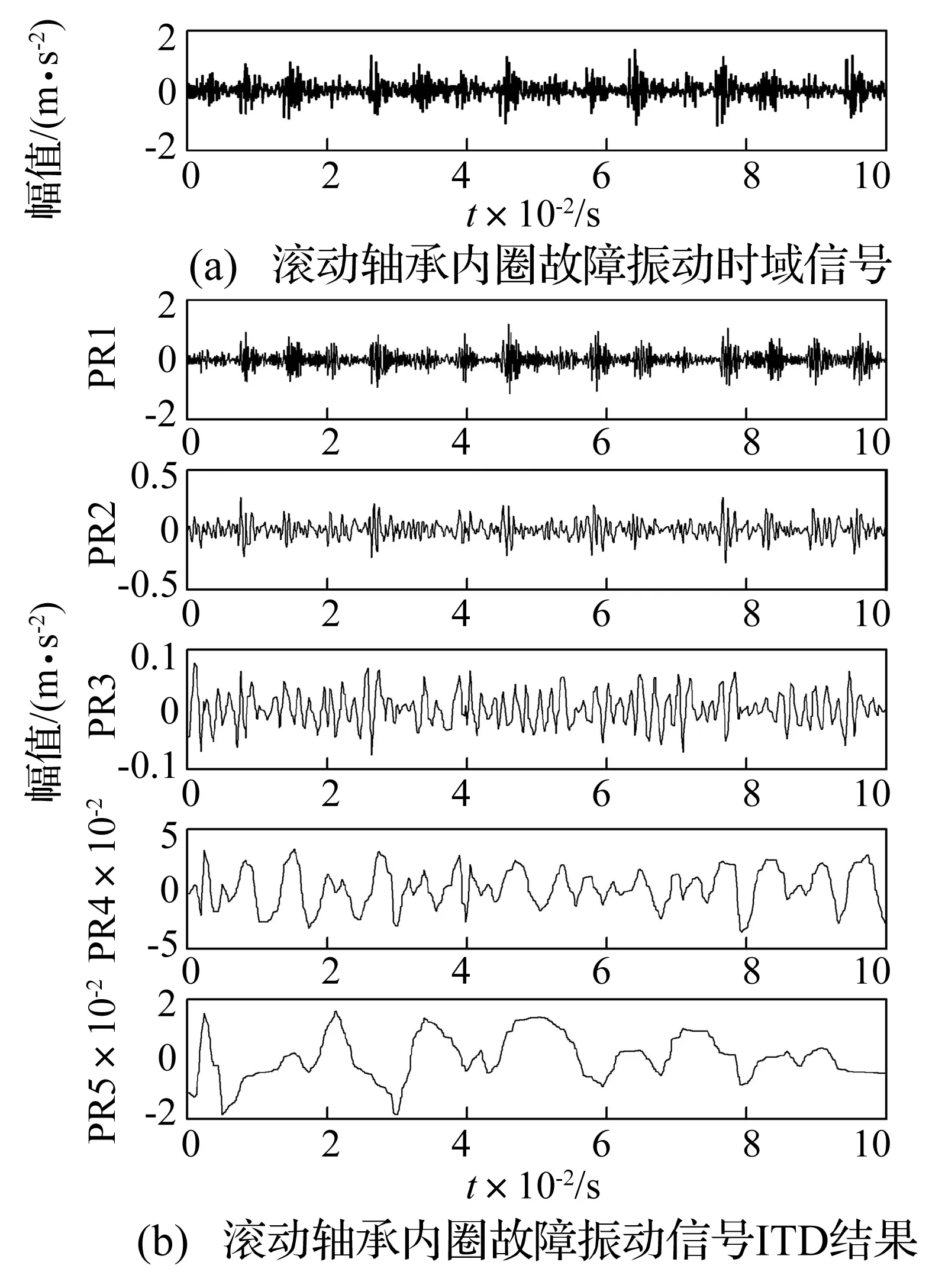
图3 滚动轴承内圈故障振动时域信号及ITD结果Fig.3 The time domain waveform and ITD result of rolling bearing with inner race fault

(3)载荷变化时，(1)、(2)特征仍然表现出来，说明PR复杂度作为特征向量具有较强的稳健性，受载荷这一外部影响小。

如图4所示为载荷为0 kW不同状态下的滚动轴承振动信号ITD分解后各PR分量复杂度的空间分布。由图4可以直观的看出，一旦滚动轴承发生故障，其特征向量所表示的样本会偏离正常状态时的样本群，这样的特性能表征滚动轴承运行状态是否正常。考虑到为了减少人为的错判，实现故障的智能识别，引入支持向量机智能分类识别方法，并使用PSO算法来优化支持向量机的核函数参数σ和惩罚参数C。

为了验证基于PSO-SVM对滚动轴承状态识别效果，采用如下测试方法：从不同载荷下的正常和三种故障状态的各100个样本中的随机选择40个作为训练样本，剩余60个样本作为测试样本，同一载荷下，对在正常和三种故障状态下的4×40组训练样本数据建立多分类的训练SVM。在训练SVM时使用了5折交叉验证方法进行训练分类准确率的验证，将交叉验证准确度取的平均值作为这一组SVM参数下分类准确度，并使用PSO算法来优化核函数参数σ和惩罚参数C以获得较高的分类准确率，最终得到训练好的SVM。将4×60组测试样本输入到训练好的SVM，测试其识别准确率。粒子群优化时采用的粒子群种群规模为20，最大迭代次数为100，学习因子为1.5。表3列出了不同载荷和状态下的对60个测试样本识别结果正确的样本个数以及该载荷下的平均识别率。由表3可知基于PSO-SVM的故障识别方法在不同载荷下，均能够有较高的准确率。该方法能够完全识别出轴承的正常状态和外圈故障状态，在内圈故障和滚动体故障方面，仅有少量样本被识别错误。

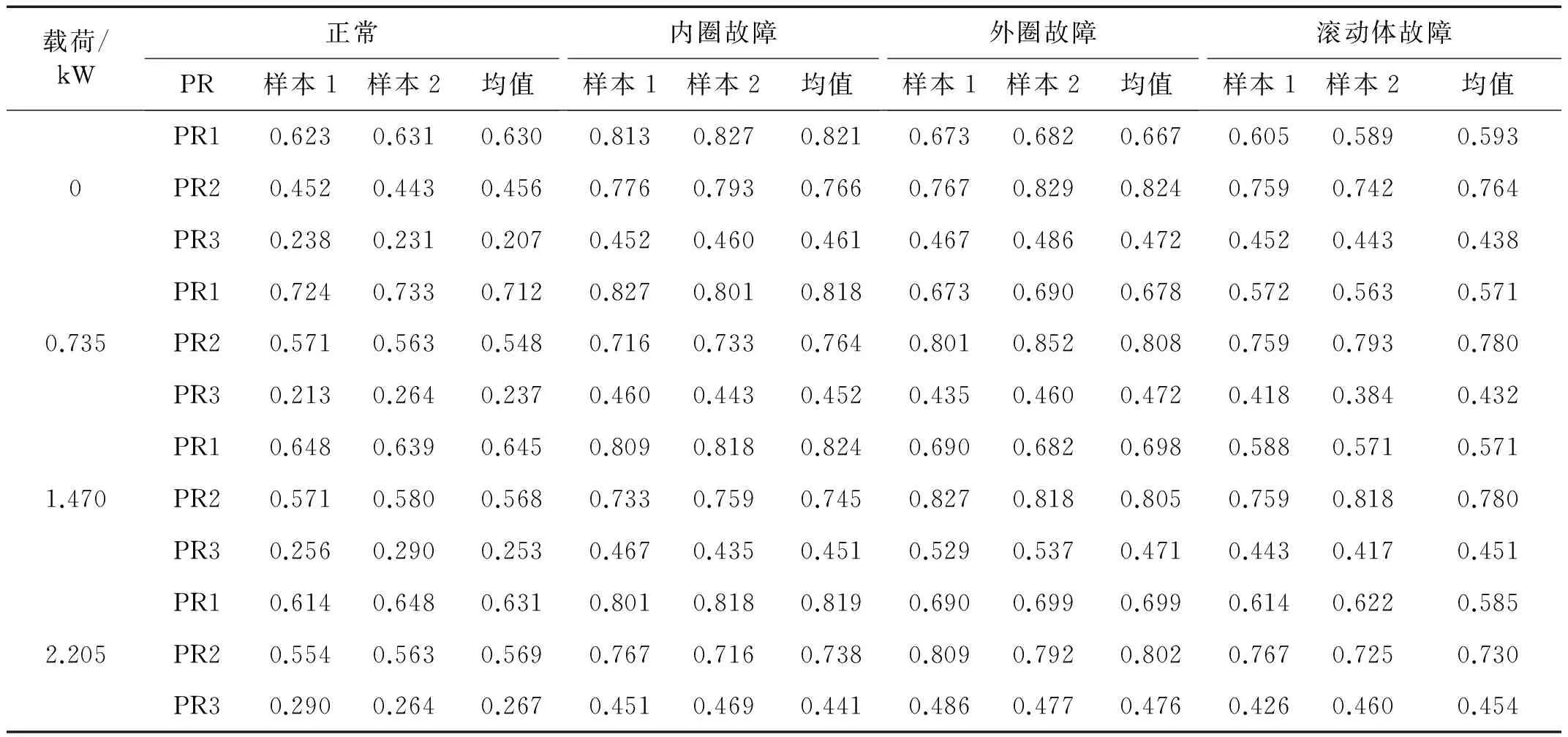
表2 滚动轴承不同载荷下Lempel-Ziv复杂度值Tab.2 The Lempel-Ziv complexity value of rolling bearings under different load

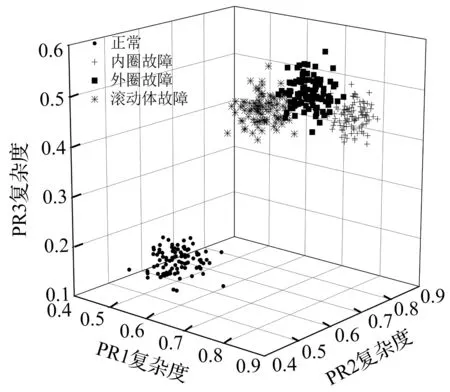
图4 不同状态下PR分量Lempel-Ziv复杂度空间分布Fig.4 Spatial distribution of PR components Lempel-Ziv complexity under different conditions

在机械设备的在线监测与诊断中，不仅要考虑分类识别算法的计算效率，还要考虑特征提取时的计算效率，若特征提取花费较多的计算时间，即使识别算法较高效也难以满足在线监测与诊断的计算时间要求。对不同载荷不同状态的轴承振动信号分解后，使用ITD的方法对信号预处理，之后分别提取Lempel-Ziv复杂度和模糊熵构建特征向量，对两种特征向量样本均使用PSO-SVM的分类方法来识别轴承状态得不同状态的平均识别率，并统计了轴承正常状态时的单个样本数据复杂度特征和模糊熵特征计算所需时间，表4所示为选用两种特征来识别轴承状态的结果对比。由表4可知，Lempel-Ziv复杂度作为特征参数时，平均准确率较高，分类效果更好，平均每个样本特征计算时间也更短。为了验证粒子群优化SVM参数构建的分类器对轴承状态识别的性能，采用ITD对不同载荷下滚动轴承不同状态的振动信号进行预处理后，计算Lempel-Ziv复杂度提取特征向量，分别采用PSO-SVM、常规的SVM、遗传算法优化SVM(GA-SVM)分类识别，表5所示为不同分类算法的识别方法对比结果，由表5可知，采用常规的SVM由于少了参数寻优的过程，与PSO-SVM相比识别时间较少，但是识别率较低。采用GA-SVM方法识别率与PSO-SVM方法的识别率较为接近，但是在参数寻优时间较长。综合可知，采用PSO-SVM进行故障识别，具备较短计算时间和较高识别率的优点。

表3 粒子群优化的SVM识别结果Tab.3 Classification result based on PSO-SVM

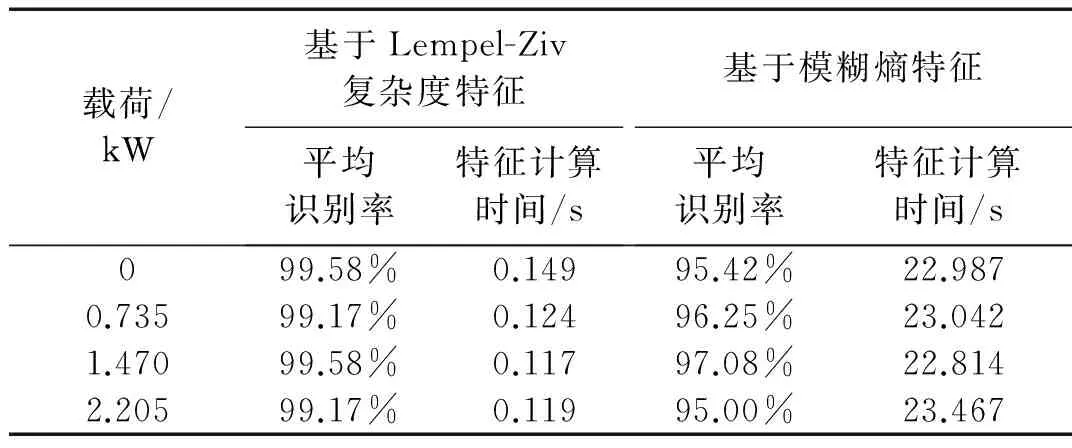
表4 Lempel-Ziv复杂度特征和模糊熵特征识别结果对比Tab.4 Classification result comparison between Lempel-Ziv complexity feature and fuzzy entropy feature

表5 不同分类算法的识别结果对比Tab.5 Classification result comparison among different classification algorithms

5 结 论

(1)针对滚动轴承非线性、非平稳振动信号特点，提出一种滚动轴承的故障诊断新方法，该方法使用ITD对滚动轴承的信号预处理，提取Lempel-Ziv复杂度作为特征向量，采用粒子群优化的SVM作为分类器。

(2)通过实验数据验证了提出的方法的有效性，实验结果表明：基于ITD的分解方法，可以自适应地将滚动轴承非平稳的振动信号分解为若干个PR分量，且在分解效率上优于EMD、EEMD方法；Lempel-Ziv可以描述滚动轴承在不同状态下的振动信号特征，这一特征向量具有稳健性，不随载荷的变化而改变；与基于模糊熵作为特征向量的诊断方法对比，Lempel-Ziv在对每个样本的特征计算时间和最终的识别结果上均优于模糊熵特征；粒子群算法寻优的参数建立的SVM对可以提高故障诊断的准确率，与遗传算法寻优对比，PSO-SVM在计算时间上优于GA-SVM分类方法。

[1] WU S D, WU P H, WU C W, et al. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine [J]. Entropy, 2012, 14(8): 1343-1356.

[2] FENG Z P, LIANG M, CHU F L. Recent advances in time-frequency analysis methods for machinery fault diagnosis: a review with application examples [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 165-205.

[3] 张立国，李盼，李梅梅，等. 基于 ITD 模糊熵和 GG 聚类的滚动轴承故障诊断[J]. 仪器仪表学报, 2014, 35(11): 2624-2632. ZHANG Liguo, LI Pan, LI Meimei, et al. Fault diagnosis of rolling bearing based on ITD fuzzy entropy and GG clustering [J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2624-2632.

[4] MARK G F, IVAN O. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 463(2078), 321-342.

[5] ZHAO S, LIANG L, XU G, et al. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method [J]. Mechanical Systems and Signal Processing, 2013, 40(1): 154-177.

[6] 苏文胜，王奉涛，朱泓，等. 基于小波包样本熵的滚动轴承故障特征提取[J]. 振动、测试与诊断, 2011, 31(2): 162-166. SU Wensheng, WANG Fengtao, ZHU Hong, et al. Feature extraction of rolling element bearing fault using wavelet packet sample entropy [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(2): 162-166.

[7] 窦东阳，赵英凯. 基于EMD和Lempel-Ziv指标的滚动轴承损伤程度识别研究[J]. 振动与冲击, 2010, 29(3): 5-8. DOU Dongyang, ZHAO Yingkai. Fault severity assessment for rolling element bearings based on EMD and Lempel-Ziv index [J]. Journal of Vibration and Shock, 2010, 29(3): 5-8.[8] HONG H B, LIANG M. Fault severity assessment for rolling element bearings using the Lempel-Ziv complexity and continuous wavelet transform [J]. Journal of Sound and Vibration, 2009, 320(1/2): 452-468.

[9] ZHANG X Y, LIANG Y T, ZHONG J, et al. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM [J]. Measurement, 2015, 69: 164-179.

[10] 李莎，潘宏侠，都衡. 基于EEMD 信息熵和PSO-SVM 的自动机故障诊断[J].机械设计与研究, 2014, 30(6):26-29. LI Sha, PAN Hongxia, DU Heng. Automaton fault diagnosis based on EEMD information entropy and PSO-SVM [J]. Machine Design and Research, 2014, 30(6): 26-29.

[11] 窦丹丹，姜洪开，何毅娜. 基于信息熵和SVM多分类的飞机液压系统故障诊断[J]. 西北工业大学学报, 2012, 30(4): 529-534. DOU Dandan, JIANG Hongkai, HE Yina. Effectively diagnosing faults for aircraft hydraulic system based on information entropy and multi-classification SVM [J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 529-534.

[12] 熊庆，张卫华. 基于MF-DFA与PSO优化LSSVM的滚动轴承故障诊断方法[J]. 振动与冲击, 2015, 34(11):188-193. XIONG Qing, ZHANG Weihua. Rolling bearing fault diagnosis method using MF-DFA and LS-SVM based on PSO [J]. Journal of Vibration and Shock, 2015, 34(11): 188-193.

[13] 窦东阳，赵英凯. 集合经验模式分解在旋转机械故障诊断中的应用[J]. 农业工程学报,2010,26(2): 190-196. DOU Dongyang, ZHAO Yingkai. Application of ensemble empirical mode decomposition in failure analysis of rotating machinery [J]. Transactions of the CSAE, 2010, 26(2): 190-196.

[14] 段礼祥，张来斌，岳晶晶. 基于ITD和模糊聚类的齿轮箱故障诊断方法[J].中国石油大学学报(自然科学版), 2013, 37(4): 133-139. DUAN Lixiang, ZHANG Laibin, YUE Jingjing. Fault diagnosis method of gearbox based on intrinsic time-scale decomposition and fuzzy clustering [J].Journal of China University of Petroleum (Edition of Natural Science), 2013, 37(4): 133-139.

Rolling bearing fault diagnosis based on ITD Lempel-Ziv complexity and PSO-SVM

ZHANG Xiaolong, ZHANG Qing, QIN Xianrong, SUN Yuantao

(School of Mechanical Engineering, Tongji University, Shanghai 201804, China)

A method for rolling bearing fault diagnosis based on intrinsic time scale decomposition (ITD), Lempel-Ziv complexity, and support vector machine (SVM) with particle swarm optimization (PSO) algorithm was proposed. The rolling bearing vibration signal was decomposed to several proper rotation (PR) components with the ITD method. The distribution of Lempel-Ziv complexity of PR components under different fault conditions was distinguishing. The Lempel-Ziv complexity of PR components was calculated to construct the feature vector for each sample. The feature vector acted as the input of SVM to accomplish the classification of different fault types. And the PSO algorithm was employed to search for the best SVM parameters to achieve higher percentage of classification accuracy. The experimental results indicate that the proposed method has the advantage of high computation efficiency and prediction accuracy without suffering from the influence of load variations.

intrinsic time scale decomposition (ITD); Lempel-Ziv complexity; support vector machine (SVM); particle swarm optimization (PSO); rolling bearing; fault diagnosis

国家科技支撑计划课题资助(2014BAF08B05)；国家自然科学基金项目(51205292)

2015-09-29 修改稿收到日期：2015-12-07

张小龙 男，博士生，1989年生

张氢 男，博士，教授，1967年生

TH133.3；TH165+.3

A

10.13465/j.cnki.jvs.2016.24.017