知识、信念与均衡——一个关于博弈均衡解理性支持系统的讨论*

李军林，王麒植，姚东旻



知识、信念与均衡
——一个关于博弈均衡解理性支持系统的讨论*

李军林，王麒植，姚东旻

均衡解；高阶信念；共同先验；不完全信息博弈

博弈理论的发展过程可以看成是对其均衡解的概念不断完善和精炼的过程，而解的概念反映的是行为和信念的一致性。在不完全信息条件下，在决策时决策者不但要考虑自己的信息，还要考虑别人的信息，别人对自己信息的信息等等高阶信念，此时如何定义信念一致性的问题长期困扰着学者。海萨尼的贡献在于通过构造“海萨尼转换”将不完全信息博弈转换为完全但不完美信息博弈，并基于此提出了贝叶斯纳什均衡的概念，为经济学建立了分析信息问题的博弈框架，并奠定了整个信息经济学的基础。本文认为，海萨尼意义上的贝叶斯纳什均衡的一致性需要以共同先验假设为前提，但是此假设在现实中很难满足。因此，在使用海萨尼博弈分析实际经济问题时，必须首先检验共同先验假设是否可以被满足。

从某种意义上讲，博弈理论的发展过程，可以看成是对其均衡解的概念(solution concept)不断完善和精炼的过程。对均衡的定义，或者说对博弈解的定义，直接反映了研究者对“理性决策”的理解。而对均衡的求解过程无非是在多人交互决策情境下，参与人根据自己已有知识并形成的信念，对理性原则的贯彻和坚持。

事实上，最初人们提到博弈论时也会很自然地将其与纳什均衡联系起来，然而，纳什均衡所要求的理性与信息约束实际上并不能很好地刻画许多常见的经济情形(例如竞标，二手车买卖，保险销售等诸多问题)，因此，需要针对此类情形构造新的解的概念以及相关的信息设定，来完善与改进博弈理论。但在放松了假设之后，如何提出合理的解的概念在博弈论发展中困扰了理论学者很长时间。其中，对于不完全信息的处理尤其棘手：由于博弈的交互性导致参与人的推理过程经常需要高阶信念(直至无穷阶信念)的支持，而如何合理、简洁地处理这些高阶信念便是建模者无法回避的问题。本文即从高阶信念和高阶知识的视角出发，分析并介绍海萨尼(Harsanyi)提出的“贝叶斯纳什均衡”(Bayesian Nash Equilibrium，后称BNE)在博弈论发展中的重大意义。[1][2][3]

在海萨尼之前，经济学没有统一的框架来分析信息问题，因此经济学分析中参与人的信息往往都是相同的。[4]海萨尼博弈对高阶信念简洁且精妙的处理，为后来的研究扫清了障碍，是方法论上的巨大突破。正是由于海萨尼的杰出贡献，使得经济学进入了前人认为“不可分析”的领域，没有他的贡献，信息经济学便永远不会产生*海萨尼的论文(参见参考文献[1][2][3])对于现代信息经济学的产生与构建是具有里程碑意义的。尽管其他一些学者关于非完全信息问题也有过奠基性的研究成果，比如，威克瑞关于拍卖竞标的论文[Vickrey,W.,“Counterspeculation, auctions, and competitive sealed tenders”,The Journal of Finance,1961 16(1)]；阿克洛夫关于二手车市场问题的论文[Akerlof, G., “The market for ‘lemons’,quality uncertainty and the market mechanism.”，Quarterly Journal of Economics, 1970,84(3),pp.488-500]；斯本斯关于劳动力市场信号传递问题的论文[Spence, M. “Job market signaling”,Quarterly Journal of Economics,1973,87(3),pp.355-374]；罗斯柴尔德和斯蒂格利茨关于保险市场销售的论文[Rothschild,M.,&Stiglitz,J.“Equilibrium in Competitive Insurance Markets:An Essay on the Economics of Imperfect Information.”,The Quarterly Journal of Economics.1976,90(4),pp.629-649]等等。尽管他们也都由于对信息经济学的杰出贡献而先后获得了诺贝尔经济学奖，但是，从研究的方法论上看，他们的工作都针对的是某个市场的特殊商品的分析而得出的结论，而海萨尼的工作是给出了非完全信息竞争市场(有不同信息行为人)一般分析框架。。

此外，他的工作在经济学说史上也是一项了不起的成就。在完全信息和非完全信息博弈分析框架建立起来之后，组织经济学、信息经济学等学科得到了极大的推动，丰富和拓展了经济学分析的视野和深度。因此，他们的贡献在学说史上也是浓墨重彩的一笔。

对博弈理论发展历程的回顾和整理对研究者正确地理解和使用相关工具具有重要意义：一方面，从现在理论发展的视角回看这些工作可以使学者更清晰完整地认识该理论根基；另一方面，对理论先驱工作的充分理解也是向其致敬的最好方式。随着泽尔腾的去世，第一批博弈论做出奠基性贡献的诺贝尔经济学奖获得者全部离我们而去。这或许意味着一个时代的结束，而本文也体现了作者对这批学者的追思。

基于此，本文介绍了博弈论围绕博弈核心问题“高阶信念和推理”进行处理的发展脉络，进而也展示知识和信念如何结合形成并支撑着具有说服力和解释力的解的概念。从这个角度将可以更好地理解、把握博弈论与经济现实的关系，以及如何进一步推动博弈论向前发展。

早期关于处理的经典博弈模型分析方法具有求解的简便性。虽然这种简便性大大提升了分析效率，从而使博弈分析工具流行起来，但同时，简便性也弱化了博弈模型背后复杂的推理过程以及假设条件，尤其可能会忽视了博弈的合理均衡解存在的理性支持系统，进而增大了模型被误用的可能。

笔者将进一步分析博弈所隐含的假设以及这些假设所对应的情形。因此，本文重点使用决策分析视角对博弈理论分析法背后的机理和假设进行阐述和分析，进而给出不同纳什均衡的理性支持系统。

一、纳什均衡与共同知识

著名的纳什均衡(Nash Equilibrium，后称NE，)是一个全部参与人的策略组合，其中每个参与人策略是在给定其他人策略不变的前提之下对自己最有利的策略。换句话说，没有一个参与人能够通过改变自己策略来改善福利水平。[5]

纳什均衡的定义中实际上隐含地引入了共同知识的假设*研究发现，博弈中的共同知识(Common Knowledge)假设在博弈均衡的定义中起到了基础性作用，但是却在现实中难以满足。因此，正确识别对被研究情形中的共同知识是选择合适博弈模型的关键。。共同知识(common knowledge)是指具有如下性质的事件：当其发生时，所有人都知道它发生了，所有人都知道其他人也知道它发生了，所有人都知道其他人都知道所有人都知道它发生了，并且此推理链条可以推到无穷阶均成立。

在完全信息条件下，勃兰登伯格对NE所要求的推理过程所蕴含的信息要求进行了总结。[6]一般来说，两类信息假设是必须的*需要注意的是，这并不意味着其他条件均无法保证纳什均衡。例如，如果要求参与人的策略是共有知识，则可以放松部分共同知识约束且仍保证纳什均衡的出现(参见参考文献[6]和[7])。：

首先，博弈的结构必须是共同知识，其中包括博弈规则、参与人数、参与人的收益等等。与单人决策过程不同，博弈过程中的决策具有交互性，即决策者的决策过程互相嵌套*例如，在两个厂商的古诺竞争中，厂商1的产量取决于自己的边际成本和厂商2的产量，而厂商2的产量又取决于自己的边际成本和厂商1的产量，形成一个嵌套循环。。博弈决策中的相互嵌套循环要求每个参与人的信念或知识也必须在无穷阶成立*参考文献[8]提供了一个清晰的例子，展示了高阶信念在博弈决策中的必要性。。很明显，完全信息假设对决策者信息的要求远不止“所有参与人都知道”特定信息，而需要参与人达成高度的一致，因而在实际生活中并不非常容易得到满足。但是遗憾的是，寻找一种合理且简便的方式放松此假设却是一项困难的任务。关于这个问题的理论发展过程将在第三部分进行讨论。

其次，所有决策者的理性方式必须是共同知识*并非在所有情形下都需要“理性”作为共同知识如此严格的条件来保证NE的出现——作为有限知识的理性即足够，参见参考文献[6]。但是为了结论不失一般性，此处仍然要求“理性”成为共同知识。。对每个决策者而言，博弈决策的交互性决定了其他决策者的决策方式也必然是影响自身决策的重要因素。下例修改自沃朗[9]的思想实验，用以说明在即使客观条件完全相同的博弈中，决策者也会根据对方参与人的不同而改变自身策略。设想你要参加一个用现金作为回报的二人博弈，并被告知将分别和两个人进行博弈，其中一位是你的朋友，另一位是陌生人。你和朋友相识多年并且智力水平相同；而那位陌生人是刚刚从喜马拉雅山上请下来的，他仅仅大概知道一块钱能买什么东西。你的可选策略有两个：唯一的纳什均衡策略和保险策略。当双方都采用纳什均衡策略时，你的收益是1 000块；但是此时如果对方偏离，你将会至少损失1 000块。如果你采用保险策略，那无论对方选择什么，你的收益都是900块。那么很明显，你面对朋友时更有可能采用纳什均衡策略。

为了保证纳什均衡的实现，在全部决策者的所有高阶信念中都必须排除出现“喜马拉雅人”的情况。换句话说，每个参与人的决策规则也必须是共同知识，也即是要求所有决策者的理性必须是共同知识。此时，“理性”实际上指的是参与人如何处理信息、作出决策的规则。

那么在实际情形下这两个条件是否容易得到满足？共同知识对参与人施加的约束十分苛刻——它要求信息不仅仅是公开的，而且必须在多个参与人中达成共识。很显然如果模型中存在重要的私人信息，那么前述推理过程必然无法成立。但是需要注意的是，并不是所有的公开信息都满足共同知识假设。例如国家宏观统计数据，虽然它是公开的，但是并不是每个人都会去看，也不是每个人都确定别人会去看，更不是每个人都确定别人知不知道自己看不看，等等。因此，若假设此类数据是参与人的共同知识，便会面临参与人行为偏离预测的风险。

此外，作为共同知识的理性也常常被忽略。例如在最后通牒博弈(Ultimatum Game)中，两个参与人(匿名)尝试就一定数量金钱达成分成比例。首先一个出价者给出他的分成计划，然后回应者决定是否接受出价者的计划。如果计划被接受，那么每个参与人获得相应的报酬；如果计划被拒绝则分成失败，两人的收益都为0。对于回应者来说，面对一个非负的计划，接受总是不差于拒绝的，因此出价者应该预测理性的回应者在此种情况下总是选择接受。然而金提思[10]通过实验研究发现低于30%的分成比经常被拒绝。这表明参与人所使用的理性原则并非总是与理论相符，对其进行预测也并不是简单的任务*另一种解释是虽然博弈规则给定了支付金额，但是却没有唯一确定每个人的效用。例如参与人可以因为分配不公平而产生副效用，从而导致拒绝成为了理性选择。如果遵从这种解释，那么实际上是各个参与人的支付而不是理性方式没有成为共同知识。这种解释是有道理的，不过却与本文提供的解释从分析逻辑上完全等价，原因在于新古典经济学以来“理性”的内含实际上是包括了“效用”和“最大化方法”两个元素的，并且二者都需要借助对方来定义自己，并不存在清晰的界限。参见[Vriend,N.J.“Rational behavior and economic theory,”Journal of Economic Behavior & Organization, 1996,29(2),pp.263-285;Binmore.K.“Chapter l-rationality,”Handbook of Game Theory with Economic Applications,2015,pp.1-26]。

总的来说，NE概念从认识论和方法论上为交互决策情形提供了有力工具，但是对于具体的情形的研究经常需要对其做更进一步的限制或扩展。接下来将介绍的贝叶斯纳什均衡用一种精妙的模型设置将NE概念的内含延伸到不完全信息情况下，而这些工作为信息经济学取得的突破性进展，在关键问题的处理上扫清了障碍。

二、共同知识与不完全信息博弈模型

(一) 不完全信息博弈与高阶信念

纳什均衡的实现所需要的大量共同知识在实际经济生活中很难满足——经济参与者往往不能对客观现实产生如此一致且正确的认识。因此在20世纪五六十年代左右，博弈论学者便提出了“不完全信息”的概念。

以如下两个简单的博弈为例，参与人1在(a)和(b)中的支付相同而参与人2的支付不同。如果参与人1不能知道参与人2的实际支付的话，他便不知道参与人2将会选L还是R，进而不知道自己的最优策略是U还是D。

表1 不完全信息

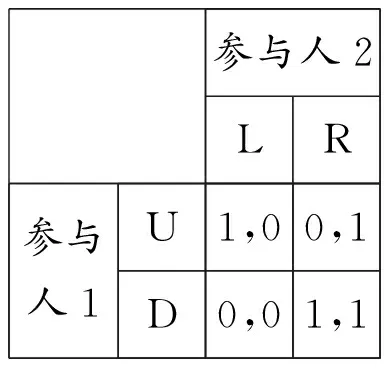
参与人2LR参与人1U1,00,1D0,01,1

(a) (b)

如果博弈中部分模型设置不是共同知识，例如上例中的支付矩阵，那么此博弈便被称为不完全信息博弈。在博弈论的发展过程中，博弈论学者对“什么是不完全信息博弈”的定义实际上发生过变化。[4]冯·诺依曼和摩根斯坦最初对“不完全信息”的定义是“部分结构没有被清晰定义的博弈” ，[11]而且从理论上讲，没有定义清楚的模型是不能被分析的，因此，他们认为没有必要研究此类博弈。显然，这个回答无法使学者们满意，许多学者此后依然在不断尝试建立新的分析方法以处理这类情形，其中最成功的尝试来自海萨尼。[1][2][3]在海萨尼的模型中，无法被精确定义的变量以概率分布的形式描述并且此分布被假设为全部参与人的共同知识。在后文的讨论中可以发现，在这些假设的帮助下，不完全信息博弈模型便是可分析的。因此，从这种意义上讲，这些变量的取值虽然不是被精确地知道，但是其取值范围以及分布是知道的，即决策者知道他们“知道自己不知道的具体是什么”和“多大程度上不知道”，因此也并不是完全不知道。换句话说，海萨尼模型所刻画的“不完全信息”已经与其最初的定义有所不同：冯·诺依曼和摩根斯坦定义的不完全信息是“不知道”，而海萨尼定义的不完全信息是“不确知”，即前者比后者包含更大的范围，如下图所示。

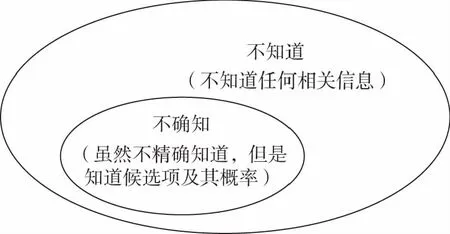
图1 两种不完全信息对比

用概率对不确定性进行刻画之后更重要的问题是高阶信念如何处理。一个直接的办法是将所有高阶信念逐阶给出，分析每种情况下的最优策略。鲁斯和拉法亚[12]曾经沿着这条思路进行了探索。为了避免完全信息的严格假设，他们为一个n人博弈构建了n2个支付函数以刻画每个参与人i对参与人j支付的推测。然而很显然，仅仅对二阶信念进行刻画是远远不足以支撑均衡的。例如，考虑表1所描述的博弈。如果在完全信息条件下，当真实支付矩阵是(a)时，参与人1将采取其纳什均衡策略D。然而，如果参与人1认为参与人2“错误地”相信真实矩阵是(b)，进而选择L的话，他也会将自己的策略修改为U。如果参与人1认为参与人2认为参与人1“错误地”相信真实矩阵是(b)，则参与人1会期待参与人2选择R，进而自己选择D。此类考虑可以无限延展下去。

因此，在不完全信息下，如何设置全部的高阶信念是一个无法回避的问题。同时也可以发现，直接给出全部信念并不是一个理想的方式，因为它十分复杂凌乱并且难以处理。海萨尼[1][2][3]介绍了一种数学上更为简便的建模方法，极大地提升了分析的可操作性。

(二)海萨尼转换与贝叶斯纳什均衡

海萨尼构造了一个由自然先行动的博弈模型，在此模型中借助贝叶斯规则便可以简便地将全部高阶信念给出，于是便解决了高阶信念的问题。海萨尼的等价构造将冯·诺依曼和摩根斯坦意义上的不完全信息博弈转换为完全信息但不完美博弈，进而避免了冯·诺依曼和摩根斯坦质疑的这种情形不可分析、相关模型不可解的问题，使分析讨论可以继续。此过程即是著名的“海萨尼转换(Harsanyi’s Transformation)”，它使不完全信息条件下的博弈分析成为可能，使经济学第一次可以使用统一规范的框架对信息问题进行分析，也为现代信息经济学的繁荣发展做出了奠基性贡献。

海萨尼首先令人信服地论证，所有对于模型的不确定性可以分为三类：对事件的不确定、对支付的不确定和对参与人策略的不确定。其次，他进一步论证这三种不确定性完全可以转化为对参与人支付的不确定性。然后，根据参与人支付的不同将参与人分为不同的“类型”，并且在正式博弈开始之前，由“自然”按照先验的概率(是共同知识)对参与人的类型进行选择，并且所有参与人仅仅可以观测到自己的类型，而不知道别人的类型。因此，虽然参与人并不确切地知道其他参与人的类型，但是可以根据先验概率和自己的类型对他们的类型进行推测(贝叶斯推断)。最后，在余下的博弈中，参与人依照自己的条件期望收益选择最优反应。以上过程被称为“海萨尼转换”，而转换后的博弈被称为海萨尼博弈。

对“海萨尼转换”过程更加准确的介绍需要引入一些概念*本文仅介绍简略定义，严格的数学定义可见[Zamir,S.,“Bayesian Games:Games with Incomplete Information,”Encyclopedia of Complexity and Systems Science,Robert A.Meyers (ed.),Springer，New York,2009,pp.426-441;Dekel,E.,& Gul,F.“Rationality and knowledge in game theory”,David M.Kreps and Kenneth F. Wallis,(eds.),Advances in Economics & Econometrics Theory & Applications Seventh World congress， Volume 1,Econometric Society Monographs,no.26,Cambridge,New York and Melbourne:Cambridge University Press,1997,pp.87-172]。。

● 自然状态(state of nature)，包含关于博弈的全部客观信息，如支付函数、博弈规则、模型中随机数的可能实现值等等。例如，表1中(a)和(b)两个博弈情形就代表了两个不同的自然状态。

● 类型(type)，包含关于博弈参与人主观信念的全部信息，因此也被称为意识状态(state of mind)。例如，参与人对真实状态是表1中哪个的信念以及全部高阶信念。

● 世界状态(state of world)，由特定的一个自然状态和特定一组参与人类型构成，描述了某个特定的博弈模型以及其中参与人的信念。

在海萨尼构造的博弈中，对“解的概念”(solution concept)的定义沿承以最优反应为核心的纳什均衡思路，又因为其对贝叶斯理性的使用，也被称为贝叶斯纳什均衡(Bayesian Nash Equilibrium, 后称BNE)。在BNE中，每个参与人都在给定其他参与人策略的条件下，选择最大化自己条件期望收益的策略。根据泽迈尔的总结，海萨尼博弈以如下顺序进行：

式中，Pr为激光回波功率，常数k为4ln2，tr为回波时刻，T0为激光脉冲宽度，Nn为噪声，包括背景噪声、电路噪声等非理想因素.其中激光回波功率可以由激光朗伯体反射传输模型得到[14]，即

1.自然选择世界状态，包括一种自然状态和全部参与人的类型；

2.参与人被告知自己的类型，但不知道自然状态和其他参与人的类型；

3.参与人选择策略并获得支付。

通过海萨尼转换，不完全信息博弈被转换成为完全但不完美信息博弈，因而模型便可以求解了。

例如，参与人1的信念为“如果自己是高能力的，那么参与人2是高能力的概率是3/7，低能力的概率是4/7；如果自己是低能力的，那么参与人2是高能力的概率为2/3，低能力的概率是1/3”*为了简洁起见，仅给出二阶信念。实际上，每一阶信念均需要满足一致性要求。；参与人2的信念为“如果我是高能力的，那么参与人1是高能力的概率是3/5，低能力的概率是2/5；如果我是低能力的，那么参与人1是高能力的概率为4/5，参与人2是低能力的概率是1/5”*双方的信念都是共同知识。。那么便可以找到一个联合分布(见表2)来描述自然的选择。在这种情况下，便称参与人的信念是一致的(consistent)。

表2 一致的信念

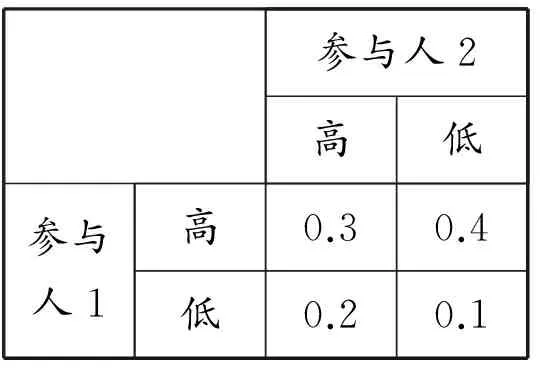
参与人2高低参与人1高0.30.4低0.20.1

可以看出，根据条件概率公式，所有的高阶信念均可以通过此联合分布得到。为了看清这一点，记高类型和低类型的参与人1为H1，L1。类似的，参与人2的类型为H2，L2。为了符号上的简便，分别记世界状态(H1，H2)，(H1，L2)，(L1，H2)和(L1，L2)为a，b，c和d。以高类型的参与人H1为例，其一阶信念可以通过计算各个世界状态条件于H1的概率得到，即真实世界状态是a的概率是3/7，是b的概率是4/7。

类似的，其二阶信念是有3/7的概率参与人2相信“世界状态是a的概率为3/5，c的概率为2/5”，有4/7的概率参与人2相信“世界状态是b的概率为4/5，d的概率为1/5”。

如果信念是一致的，或者说，存在共同先验，那么在贝叶斯理性(利用条件概率进行推断)的帮助下，所有的高阶信念均是共同知识。也就是说，此时，博弈模型以一种简洁的方式重新成为了“完全的”(complete)，并且可以通过条件概率公式计算出每一阶信念，避免了直接考虑高阶信念时所面对的复杂又难以处理的数学运算。在“共同先验假设”的保证下，BNE便可以被清晰地定义*此定义非常基础，可在任意博弈论教材中找到，因此本文略去介绍。。

由于海萨尼的工作，后继的研究可以轻易地对信息问题进行分析而不用涉及复杂的高阶信念问题。这一贡献是奠基性的，它在不增加过多的数学复杂性的前提下，直接拓展了经济学研究的范围，为理解更加复杂的博弈互动行为提供了有力的分析工具。

此外，了解海萨尼转换的前提也同样重要。通过上例可以看到，海萨尼转换要求信念的一致性。如果信念不是一致的，便无法找到一个作为共同知识的联合分布，因此分析过程就会变得更加复杂。需要注意的是，海萨尼转换并非适用于为所有的不确定性和关于不确定性的信念情形建模，作为对海萨尼工作的补充，下一节将考察不一致信念的问题。

(三) 信念的一致性问题

如果将上述参与人2的信念前半部分修改为“如果我是高能力的，那么参与人1是高能力的概率为1/2，参与人2是低能力的概率是1/2”，此时，便不存在可以支撑1和2信念的联合分布*此例修改自Zamir,S.,“Bayesian Games: Games with Incomplete Information”,Encyclopedia of complexity and Systems Science,Robert A.Meyers(ed.),Springer，New York,2009,pp.426-441.。那么，便不存在一个公认的自然选择过程作为起点，海萨尼转换无法适用。在这种情况下，便称参与人的信念是不一致的。

显然，海萨尼转换所需要的重要假设是全部参与人的信念是“一致的”，即可以从共同的先验概率中推得，并且此先验概率分布是共同知识。此假设被称为共同先验假设(Common Prior Assumption，后称CPA假设)，满足此假设的博弈被称为海萨尼博弈。显然，并不是所有的博弈都是海萨尼博弈。也就是说，为了分析更广泛的博弈情形，需要一个比海萨尼博弈中定义的BNE更加一般的解的概念。

实际上，BNE的定义并不一定要以海萨尼转换(或一致性信念)为基础。如上例中的不一致的信念可表示如下：

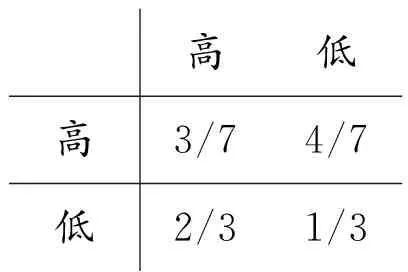
高低高3/74/7低2/31/3

(a)参与人1的信念

高低高1/24/5低1/21/5

(b)参与人2的信念

假设四种情形下参与人的支付矩阵为：

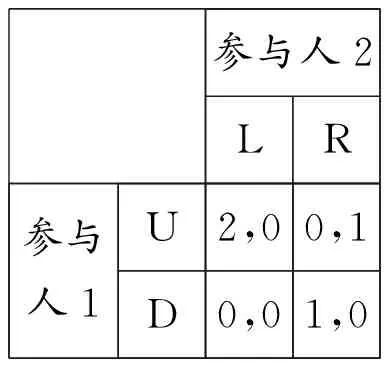
参与人2LR参与人1U2,00,1D0,01,0

GHH：参与人都是高能力时的支付矩阵

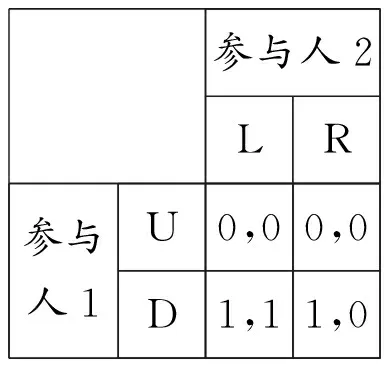
参与人2LR参与人1U0,00,0D1,11,0

GHL：参与人1是高能力且参与人2是低能力时的支付矩阵

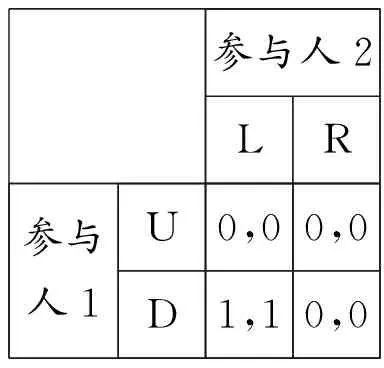
参与人2LR参与人1U0,00,0D1,10,0

GLH：参与人1是高能力且参与人2是低能力时的支付矩阵

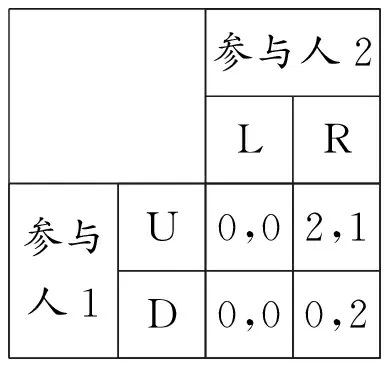
参与人2LR参与人1U0,02,1D0,00,2

GLL：参与人都是高能力时的支付矩阵

由于信念的不一致性，无法使用海萨尼转换，但是此博弈仍然有混合策略均衡。将参与人1的策略记为(x,y)，表示：

● 当参与人1是高能力时，使用混合策略[x(U), (1-x)(D)]；

● 当参与人1是低能力时，使用混合策略[y(U), (1-y)(D)]；

类似的，将参与人2的策略记为(z,t)。在混合策略均衡下，每个参与人的每个类型必须对自己的两个纯策略无差异。因此解得：

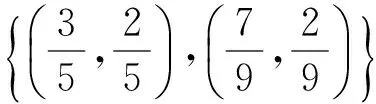
可以看出，CPA所要求的前提实际上十分严格，它不仅要求参与人对“不知道”的事件形成概率层面的认识，更要求这种概率层面的认识是一致的且是共同知识。换句话说，它要求参与人对不知道的事情达成一致。一致性信念的要求很重要，因为即使参与人的信念是共同知识，但是如果他们不一致，海萨尼意义下的BNE依然不适用。而在现实生活中，我们往往很难说清CP是从哪来的。CP所刻画的情形中参与人都必须十分熟悉且达成了思想层面的高度一致。所以，实际上海萨尼意义下的BNE的适用范围十分局限，并不是任意的情形都可以适用。若要适用海萨尼博弈作为分析框架，必须首先验证是否所要模型化的情境之中存在CP的基础*参考文献[14]证明了在所有可能的信念系统集合(belief system)中一致性信念系统集合的勒贝格测度为0。也就是说，海萨尼转换所依赖的一致性信念系统并非是一个容易满足的条件。。

为了解决信念不一致的问题，默滕斯和泽迈尔[15]提出了信念空间(BeliefSpace)的模型，并将在信念空间上重新定义BNE。在信念空间中，并不要求信念是一致的，进而大大拓展了分析范围。然而，这种方法所使用的数学技术较为复杂，在实际研究中，研究者总是希望能利用共同知识来简化模型。总的来说，CPA的合理性在经济学界仍然是一个有争议的话题*对这个问题的讨论可参见[Dekel,E.,& Gul,F.Rationality and knowledge in game theory，Advances in Economics & Econometrics Theory & Applications Seventh world Congress， Volume 1, Econometric Society Monographs,no.26,David M. Kreps and Kenneth F. Wallis,(eds.)，Cambridge, New York and Melbourne:Cambridge University Press,1997,pp.87-172;Morris,S.，“The common prior assumption in economic theory，” Economics & Philosophy, 1995,11(2),pp.227-253;Gul,F.,“A Comment on Aumann’s Bayesian View, ”Econometrica,1998,Vol. 66, No.4,pp.923-927],对CPA假设的质疑，以及奥曼(Aumann,R.J.“Common Priors: A Reply to Gul,”Econometrica,1998,Vol.66,No.4,pp.929-938)为CPA的辩护。。

三、总结性评述

海萨尼贡献的直接产物之一便是现代信息经济学。从以上对海萨尼模型的简单梳理过程便可以很清晰地发现，现代信息经济学分析必须遵从海萨尼模型的前提假设。研究者若要用不完全信息博弈模型对现实进行刻画分析，则必须先验证这些假设是否能被满足。一旦不满足，则必须对标准模型进行修改或建立新模型。一个严重的建模误区是将部分假设看成“建模惯例”而不对其深究。CPA便是一个很好的例子：虽然现实生活中能满足CPA的情形十分有限，但是在分析中对其的使用则显得有些任意。正如宾莫尔[16]所强调的：海萨尼仅仅告诉我们满足CPA的模型该如何处理，但没有告诉我们哪些情况满足它。对模型假设的详细验证不仅保证模型对现实的准确刻画，而且还帮助研究者正确地解释结论并排除那些由不合理假设带来的“有趣”结论。

一个值得注意的问题是，虽然不完全信息最初被引入是为了放松“共同知识”对博弈参与人过于苛刻的要求，但是在海萨尼模型中对CPA的依赖实际上完全背离了这一初衷：共同知识的假设完全没有被放松，甚至可以说是更加严格了。在不完全信息博弈中，CPA假设要求参与人对不知道的事情也要达成一致，即确切地知道别人是如何不知道的、以什么概率认为是什么情况等等信息。这种一致明显更难以达成。此外，由于贝叶斯推断的复杂性远远高于一般选择理论对决策者的理性要求，所以，奥曼认为不完全信息博弈并非体现了决策者的有限理性，而是一个要求超级无限理性的模型。这也导致不完全信息博弈的理论预测结果可能与现实情况产生偏差。

总结来说，纳什均衡的思路在非合作博弈中得到了很好的继承和延续。同时，纳什均衡所要求的严苛前提条件在后续的博弈研究中也并没有得到缓解，反而，以海萨尼博弈为例，甚至被限定得更加苛刻了。因此，研究者在利用博弈论对现实问题进行考察的过程中，必须仔细验证这些条件是否得到了满足，从而保证分析的合理性。

[1]Harsanyi,J.C.Gameswithincompleteinformationplayedby“Bayesian”players, Ⅰ-Ⅲ.PartI.Thebasicmodel[J].ManagementScience,1967,(14).

[2]Harsanyi,J.C.Gameswithincompleteinformationplayedby“Bayesian”players,Ⅰ-ⅢPartII.Bayesianequilibriumpoints[J].ManagementScience,1968a,(14).

[3]Harsanyi,J.C.Gameswithincompleteinformationplayedby“Bayesian”players,Ⅰ-ⅢPartⅢ.Thebasicprobabilitydistributionofthegame[J].ManagementScience，1968b,(14).

[4]Myerson,R.B.Commentson“GameswithIncompleteInformationPlayedby‘Bayesian’Players,I-IIIHarsanyi’sGameswithIncompleteInformation”[J].ManagementScience,Vol. 50,No. 12Supplement,December2004.

[5]Nash,J.Non-cooperativegames[J].AnnalsofMathematics, 1951,(54).

[6]Brandenburger,A.Knowledgeandequili-briumingames[J].TheJournalofEconomicPerspectives,Vol.6,No.4,1992.

[7]Aumann,R., &Brandenburger,A.EpistemicConditionsforNashEquilibrium[J].Econometrica,1995，63(5).

[8]Binmore,K.Playingforreal[M].Oxford:OxfordUniversityPress,2007.

[9]Werlang,S.R.D.C.Commonknowledgeandgametheory[Z].PhDDissertation,PrincetonUniversity，1986.

[10]Gentis,H.GameTheoryEvolving[M].Princeton,NJ:PrincetonUniversityPress,2000.

[11]VonNeumann,J.,Morgenstern,O.TheoryofGamesandEconomicBehavior[M].Princeton,NJ:PrincetonUniversityPress,1944.

[12]Luce,R.D.andRaiffa,H.GamesandDecisions[M].Wiley,NewYork,1957.

[13]Zamir,S.BayesianGames:GameswithIncom-pleteInformation[A].RobertA.Meyers(ed.).EncyclopediaofComplexityandSystemsScience[C].Springer;NewYork,2009

[14]Nyarko.Mostgamesviolatethecommonpriorsdoctrine[J].InternationalJournalofEconomicTheory,2010,6(1).

[15]Mertens,J.F., &Zamir,S.FormulationofBayesiananalysisforgameswithincompleteinformation[J].InternationalJournalofGameTheory, 1985,14(1).

[16]Binmore.K.Chapter1-rationality[Z].HandbookofGameTheorywithEconomicApplications, 2015.

[责任编辑 陈翔云]

Knowledge, Belief and Equilibrium——A Discussion on the Belief System of Solution Concept

Li Junlin1, Wang Qizhi2, Yao Dongmin3

(1,2. School of Economics, Renmin University of China, Beijing 100872; 3. Center for China Fiscal Development， Central University of Finance and Economics, Beijing 100081)

equilibrium solution; high-order belief; common prior; incomplete information game

The development of game theory can be regarded as a process of continuous improvement and refinement of the solution concept, which imposes consistency requirements on behaviors and beliefs. Harsanyi’s contribution is converting a game of incomplete information to a complete but imperfect information game by “Harsanyi transformation”, and proposing the concept of Bayesian Nash equilibrium, which provided an unified analytical framework to cope with information problem and laid the foundation for the economics of information. This paper argues that the Bayesian Nash Equilibrium defined on the Harsanyi game needs to take the common prior assumption as the premise, which is rather demanding. Therefore, any analysis based on the Harsanyi game must make sure the common prior assumptions are satisfied.

李军林，中国人民大学经济学院教授，中国特色社会主义经济建设协同创新中心研究员；王麒植，中国人民大学经济学院博士生(北京 100872)；姚东旻(通讯作者)，中央财经大学中国财政发展协同创新中心讲师(北京100081)。

* 作者李军林感谢近年来在博弈论专题课堂上积极参与讨论的各位博士生、硕士生同学。