高速铁路接触网拉出值和定位器坡度优化研究

罗 健，蒋冀龙

(铁道第三勘察设计院集团有限公司，天津 300251)



高速铁路接触网拉出值和定位器坡度优化研究

罗 健，蒋冀龙

(铁道第三勘察设计院集团有限公司，天津 300251)

高速铁路接触网定位器与受电弓的相对位置关系直接影响弓网运行安全。通过合理设置拉出值和定位器坡度，既能保证弓网受流性能和弓网安全，又能降低受电弓滑板的损耗。通过对直线、曲线区段跨距值、拉出值、定位器坡度、第一吊弦点位置之间的相互关系进行详细研究，为高铁接触网设计优化提供依据。通过研究，在接触网其他主要设计参数一定的情况下，得出针对直线、曲线区段的不同跨距下拉出值的推荐设置，在保证定位器具有合理坡度值的同时，使得受电弓与定位器的匹配关系更加安全可靠，可指导工程设计。

高速铁路；接触网;定位器;坡度控制;拉出值

在高速铁路中，弓网关系的好坏不仅关系到列车的安全、稳定、高速运行，而且还在很大程度上影响着接触网、受电弓的使用寿命。一方面，受电弓在高速运动过程中对接触悬挂产生一定激扰，对接触悬挂的疲劳寿命有着较大的影响；另一方面，接触线、受电弓滑板这对滑动摩擦副的磨耗，与两者的相对硬度、相对几何位置以及弓网离线率大小等因素有着密切的关系[1-3]。

目前高速铁路受电弓滑板绝大多数采用碳滑板，接触线采用铜合金导线，两者布氏硬度接触线较高，从理论上讲，这样的配置有利于减少接触线的磨耗[4-5]。受电弓与接触线的相对几何位置，主要受控于接触导线的拉出值。拉出值是指接触线在定位点处与受电弓中心的距离，在直线区段一般垂直线路方向向两侧拉出，按“之”字形布置，其目的主要是避免受电弓滑板的不均匀磨损并使接触悬挂具有较好的风稳定性[6-7]。接触线拉出值的大小与方向，主要影响接触悬挂风偏值、定位器的坡度值和受电弓滑板的磨损范围[8-9]。

国内设计、施工、验收有关规范未对拉出值、定位器坡度值作出明确规定，拉出值从200～300 mm设置不一，各设计院对定位器坡度控制要求也不尽相同，在设计中很少统筹考虑跨距、拉出值、第一吊弦位置对定位器坡度的影响，往往设计提出的定位器坡度控制要求在工程施工中无法实现。因此，有必要对高速铁路接触网拉出值设置、定位器坡度及控制要求等重要参数进行深化研究，厘清跨距、拉出值、定位器坡度、第一吊弦位置等的相互关系，优化设计，提出合理、可行的参数设置方案，提高弓网运行的安全性。

1 定位器坡度控制要求分析

定位器在接触网系统中用于固定接触线的位置，在直线区段，使接触线沿线路走向呈“之”字形布置[10]。定位器坡度可以用定位器支座中心和接触线底面连线与受电弓平面的夹角表述，也可以用定位器支座中心和接触线底面连线与水平面的夹角表述，二者可通过轨道外轨超高进行转换，本文中的定位器坡度用前者表述。对于限位定位器，定位器坡度等同于定位器本体与受电弓平面的夹角。定位器坡度是由接触网系统参数决定的，在设计中要统筹考虑定位器坡度值对受电弓安全、接触线偏磨等的影响。

1.1 受电弓安全

为保证受电弓的安全运行，在任何时候，定位器不应侵入受电弓动态包络线，且应有一定的安全裕度，直形定位器坡度值与受电弓的相互位置关系见图1～图3[11]。

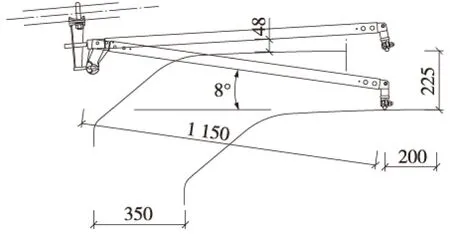
图1 定位器坡度8°安全校验(单位：mm)

图2 定位器坡度6°安全校验(单位：mm)

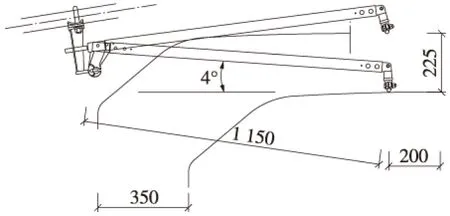
图3 定位器坡度4°安全校验(单位：mm)

受电弓按UIC 608 Annex 4a标准宽度1 950 mm，弓头工作宽度为1 450 mm[12]。横向摆动量按直线区段250 mm、曲线区段350 mm设计，动态最大抬升量150 mm[13]。限位定位装置安装设计按不小于1.5倍动态抬升量进行安全校验[13]。

从图中可以看出，定位器坡度越小，越不利于安全校验。当定位器坡度为4°时，按照1.5倍动态抬升量校验，定位器本体侵入受电弓动态包络线，安全校验不通过。在同等坡度情况下，如采用弧形定位器，会增大定位器与受电弓间的安全距离。

1.2 接触线偏磨

为防止接触线偏磨，应使接触线顶面中心与底面中心连线垂直于受电弓平面，在定位器管与定位钉套筒制造角度为98°[14]的情况下，定位器坡度宜控制在8°左右。

从上述分析可以看出，考虑空间安全裕度，定位器坡度应取较大值；考虑减少接触线偏磨，定位器坡度以8°为宜。综合两方面考虑，定位器坡度宜控制在8°，后文将从其它方面做深入研究。

2 定位器坡度计算

2.1 定位器受力分析

定位器一端安装于定位支座，另一端安装于接触线，安装稳定后达到力的平衡状态。根据定位器工作状态，建立力学模型，进行定位器坡度受力分析，见图4。从受力分析可以看出，定位器主要受接触线作用于定位线夹处的拉力FJ，定位支座作用于定位器根部的拉力Fzz，及定位器自身重力Gdw和定位线夹自身重力Gxj。

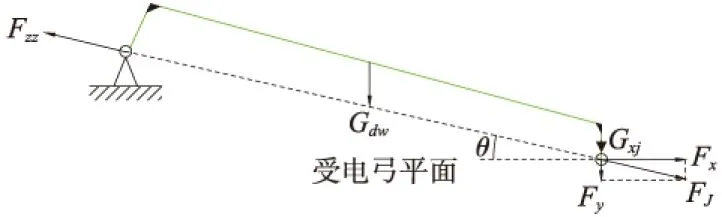
图4 定位器受力分析

定位器坡度为

θ=arctan((Fy+Gdw/2+Gxj)/Fx)

其中，Fx为FJ的水平分量;Fy为FJ的垂直分量

从上式可以看出，Fx和Fy是计算定位坡度的关键参数。Fx可以在接触网水平面内按矢量合成的方式进行计算，见图5。

图5 定位点水平力分析

其中，α为定位点处接触线夹角，其大小与拉出值、跨距值相关；Sj为接触线张力。

Fy即接触线作用于定位器上的垂直力，可以在链型悬挂系统模型中计算得到，见图6。

图6 吊弦点(定位点)垂直力分析

图6中，Leni为第i个跨距的长度；Ln为第n吊弦所在位置的水平坐标，n=1，2，…，MN，N为每跨的吊弦数，M为模型内的跨距数；Sj为接触线水平张力；L为锚段长度；Sc为承力索水平张力。

对于接触线，假设第n根吊弦或定位点处接触线的抬升量为Δyn。Δyn为吊弦或定位点处接触线相对于锚段起点接触线水平高差，它受到竖曲线、外轨超高及导高变化等因素的影响。第n吊弦的拉力或者定位器受力的垂直分量Tn。参照《链形悬挂系统静态弹性的解析计算》[15]可得方程组

通过求解方程组(1)可以得到每个吊弦的拉力Tn，其中包括定位器受力的垂直分量Fy。

2.2 计算输入条件

接触网采用全补偿弹性链型悬挂，接触悬挂线材为JTMH120+CTMH150，张力为21 kN+30 kN[16]；直形限位定位器，长度1 150 mm；跨距(L)50～60 m；拉出值(A)200～300 mm，第一吊弦距定位点距离(L1)一般取5～6 m，困难时4～7 m[17]；线路曲线半径7 000～12 000 m；超高按照350 km/h线路标准设置[18]。

2.3 直线段定位器坡度计算与分析

根据定位器受力分析原理，建立数学模型，编制计算软件，对直线段定位器坡度、拉出值、跨距等参数进行计算。结果见表1。

表1 直线计算结果

从表1可以看出，在跨距和拉出值一定的情况下，第一吊弦点与定位点距离越大，定位器坡度越大；在跨距和第一吊弦点位置一定的情况下，拉出值越小定位器坡度越大；在拉出值和第一吊弦点位置一定的情况下，跨距越大定位器坡度越大。

2.4 曲线段定位器坡度计算与分析

同理，对曲线段定位器坡度、拉出值、跨距等参数进行计算。以曲线半径12 000、9 000、7 000 m为例，计算结果见表2～表4。

从上述结果可以看出，在相同跨距、拉出值、第一吊弦点位置的情况下，曲外的定位器坡度显著小于曲内。因此，为使曲内、曲外定位器坡度都满足标准要求，可通过曲内、曲外设置不同的第一吊弦点位置来解决。

3 拉出值和定位器坡度控制优化方案

根据上述计算结果，针对直线、曲线区段的不同跨距，按照定位器坡度优先8°～9°，最小7°，最大14°，第一吊弦间距优先按5～6 m，困难4～7 m，以拉出值尽量大的次第优先原则进行选取，推荐的配置见表5。其中曲线半径7 000 m，跨距60 m、65 m时，定位器坡度超出上述范围，故此时只能采用50～55 m跨距。

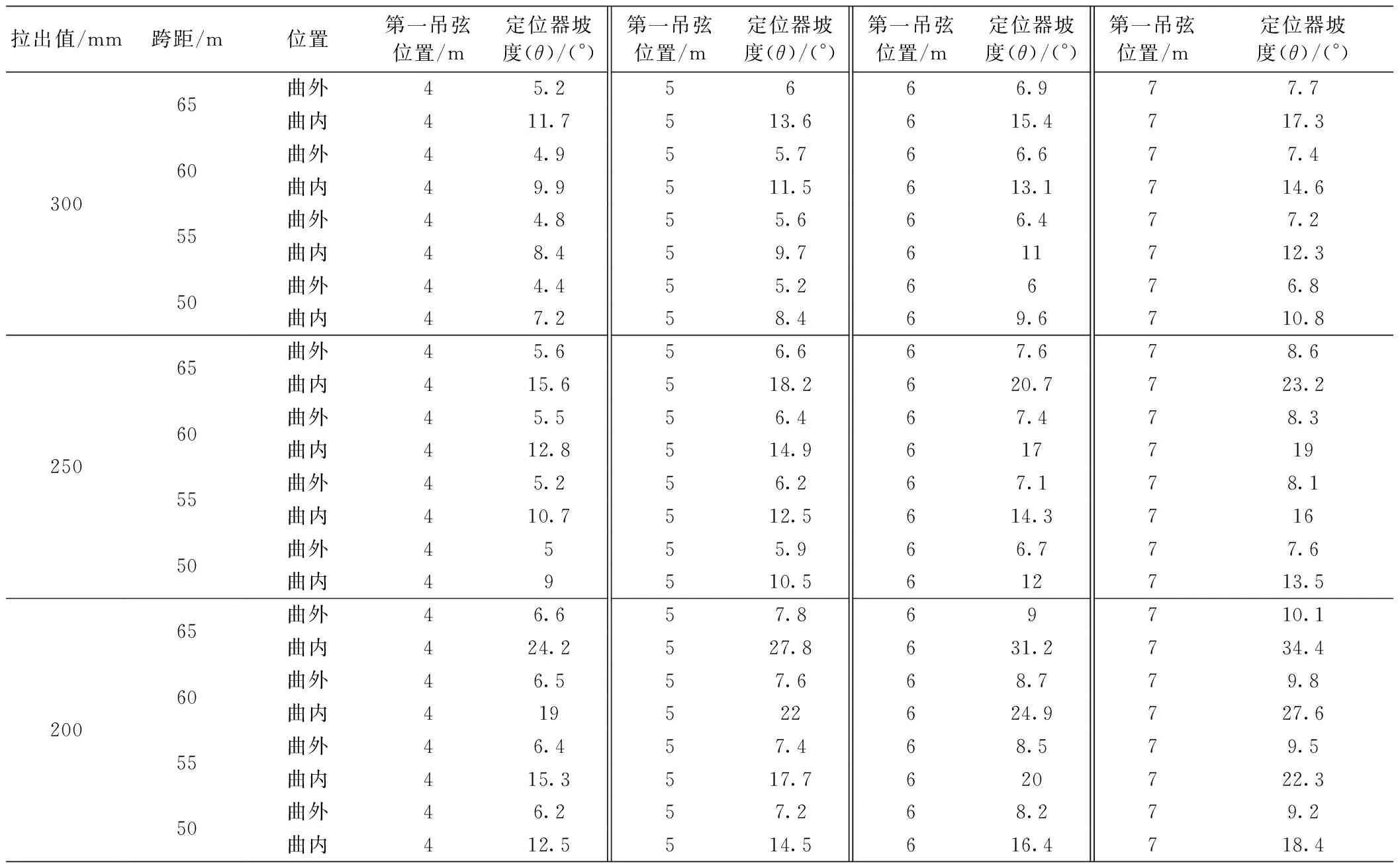
表2 曲线半径12 000 m计算结果

表3 曲线半径9 000 m计算结果

表4 曲线半径7 000 m计算结果

表5 拉出值和第一吊弦点布置

4 结论与建议

基于常用的接触网系统参数配置，通过对第一吊弦点位置、拉出值、跨距、定位器坡度的相互关系进行研究，得出在不同曲线半径和跨距下推荐的拉出值设置，使得受电弓与定位器的匹配关系良好，且滑板磨耗较为均匀，能有效地延长碳滑板的寿命，具备良好的技术经济性。

通过本次研究发现，定位器的外形尺寸和工作范围对跨距、拉出值的设置有较大影响，建议研究采用非限位的弧形定位器，使跨距、拉出值的选取更加灵活。

[1] 张跃新.高速电气化铁路接触网施工技术研究[D].西南交通大学，2006.

[2] 关金发，吴积钦.城市轨道交通弓网系统现状分析与建议[J].铁道标准设计，2016(1):144-147.

[3] 朱飞雄.欧洲铁路接触网受电弓系统兼容标准及其影响[J].铁道标准设计，2005(6):97-100.

[4] 胡艳，董丙杰，黄海，等.碳滑板/接触线摩擦磨损性能[J].交通运输工程学报，2016，16(2).

[5] 王健，胥燕军，汪力，等.机器视觉在钢轨磨耗检测中的应用研究[J].铁道标准设计，2014(9):36-39.

[6] 于万聚.高速电气化铁路接触网[M].成都：西南交通大学出版社，2002.

[7] 刘改红.接触网参数对接触网风致响应的影响及风洞试验验证[J].铁道标准设计，2016(2):144-148.

[8] 肖长春.接触线风偏与拉出值的相互影响分析[J].科技创业月刊，2010(12):231-232.

[9] 韩佳栋.高速铁路接触网风致振动与风偏的动态计算方法[J].铁道标准设计，2016，60(6).

[10][德]基布岭，等.电气化铁道接触网[M].中铁电气化局集团有限公司，译.北京：中国电力出版社，2003.

[11]罗健.高速铁路接触网定位器坡度问题的深化研究[J].铁道工程学报，2013(1)：76-80.

[12]隋延民.接触网定位器坡度计算及定位安全措施[J].铁道工程学报，2011(4)：75-78.

[13]中华人民共和国铁道部.TB10020—2009高速铁路设计规范(试行)[S].北京：中国铁道出版社，2010.

[14]中华人民共和国铁道部.TB/T 2075—2010电气化铁路接触网零部件[S].北京：中国铁道出版社，2010.

[15]白裔峰，等.链形悬挂系统静态弹性的解析计算[J].中国铁道科学，2011，32(1):95-101.

[16]中华人民共和国铁道部.TB 10758—2010高速铁路电力牵引供电工程施工质量验收标准[S].北京：中国铁道出版社，2010.

[17]中华人民共和国铁道部.TB 10009—2005铁路电力牵引供电设计规范[S].北京：中国铁道出版社，2005.

[18]中华人民共和国铁道部.TB 10760—2013高速铁路工程静态验收技术规范[S].北京：中国铁道出版社，2013.

Study on Stagger Value and Steady Arm Slope of High Speed Railway Catenary

LUO Jian， JIANG Ji-long

(The Third Survey and Design Institute Group Corporation, Tianjin 300251, China)

The correlation between steady arm and pantograph of high speed railway is crucial to the safety of railway operation. Rational stagger and steady arm slope play an important role in obtaining good current-collection and safe operation of the pantograph-catenary system and reducing the wear of the pantograph strip. This paper conducts a detailed study on the span length, the stagger, the slope of steady arms and the first dropper position in both tangent and curve lines, providing references for the design and optimization of high speed railway catenary. Given the major design parameters of catenary system, the paper offers recommended stagger values with respect to different curvature radiuses and different spans, which makes it possible to achieve proper slope of steady arm and better matching performance of steady arm and pantograph. The solution may guide the engineering design.

High speed railway; Catenary; Steady arm; Slop control; Stagger

2016-08-31

中国铁路总公司科技研究开发计划项目(2015J005-D)。

罗 健(1980—)，男，高级工程师， 2003年毕业于西南交通大学机械工程及自动化专业，工学学士，E-mail:9195025@qq.com。

蒋冀龙(1992—)，男，2016年毕业于兰州交通大学土木工程专业，工学学士，E-mail:2108016505@qq.com。

1004-2954(2016)12-0140-05

U238； U225

A

10.13238/j.issn.1004-2954.2016.12.031