跨座式单轨列车-轨道梁耦合动力学特性研究
2021-09-10马湿洪
马湿洪

摘要:跨座式单轨列车-轨道梁系统的耦合振动问题涉及因素多,有待进一步研究。基于刚柔耦合理论建立跨座式单轨列车-轨道梁耦合动力学模型,以探讨不同轨道梁跨距和载重状态对系统响应的影响。结果表明:轨道梁跨中竖向挠度和横向挠度均随跨距的增加而增大,跨中竖向挠度影响更显着;跨中竖向挠度随载客量的增大而增大,横向挠度基本不受载客量的影响。研究可为跨座式单轨交通系统的结构设计优化和运输管理提供理论基础。
关键词:跨座式单轨;列车-轨道梁耦合;跨距;载重;运行平稳性
中图分类号:U441 文献标识码:A 文章编号:1674-957X(2021)05-0040-02
0 引言
列车和轨道梁结构之间形成了一个相互作用、相互影响的多自由度振动系统,但目前针对跨座式单轨-轨道梁耦合动力学模型及特性的研究仍然匮乏。KenjiroGoda[1]教授建立三自由度跨座式单轨车辆-轨道动力模型,对单轨车辆曲线通过性能进行仿真,结果表明机车车辆转向架导向轮径向力大于拖车车辆转向架导向轮径向力。C.H.Lee等[2]建立了15自由度车辆模型,并采用模特叠加法建立了桥梁分析模型,以研究车速、旅客数量等因素对旅客舒适性的影响。并在另一研究中提出了轨道梁的横向位移来源于桥梁剪心与列车竖向荷载偏心引起的扭转效应[3]。
基于以上研究,本文分析了跨座式单轨车辆一轨道梁动力相互作用机理,基于刚-柔耦合理论,建立跨座式单轨列车-轨道梁空间耦合动力学分析模型。探讨了不同轨道梁跨距和载重状态对耦合系统振动响应的影响水平。
1 跨座式单轨列车-轨道梁耦合动力学模型
1.1 跨座式单轨车辆动力学子模型
对于单节单轨车辆,通常将车体、前后转向架视为刚体,忽略其弹性变形影响,其中车体和转向架相对于总体惯性坐标系都具有2个平动和3个转动自由度,分别为横移(y)、沉浮(z)、側滚(φ)、摇头(ψ)和点头(θ)运动,共15个自由度。基于拉格朗日方程对15自由度车辆模型进行建立:
1.1.1 车体横移、沉浮方程
(1)
(2)
1.1.2 前、后转向架横移、沉浮方程
(3)
1.2 轨道梁振动模型
本文基于有限元法建立轨道梁空间振动模型,均采用空间离散梁单元,每个节点有6个自由度。其基本思路是,首先将复杂的轨道梁结构离散成有限个单元的集合体,然后在各自单元内选择合适的位移模式,并计算每个单元及整个轨道梁结构的动能和应变能,再由Hamilton原理推导出轨道梁结构振动无阻尼微分方程,最后采用Craig-Bampton固定界面模态综合法进行轨道梁结构振动响应的求解。因此,轨道梁有限元模型的无阻尼运动方程可表示为:
(4)
式中:Mb、Kb分别为质量、刚度矩阵;ub为节点位移向量;Fb为荷载列向量。
基于Craig-Bampton法,将子结构的位移划分为结构内部节点位移ui和界面节点位移uj,故式(5)无阻尼运动微分方程可改写为分块矩阵形式:
(5)
式中:F内部节点处内力矩阵;F为界面处的内力矩阵。
式(6)经过坐标转换,以振型叠加项来替代位移矢量,经过方程简化可得到运动方程的简化形式为:
(6)
引入模态矩阵φb和模态坐标qb,其节点位移可表示为:
(7)
式中:φm为主模态矩阵;φn为约束模态矩阵;qb为提取的模态数。
1.3 轮胎模型
本文选择基于弹性地基梁理论的FIALA轮胎模型来描述走行轮、导向轮、稳定轮的力学行为。根据FIALA轮胎模型,轮胎侧向力方程可以表示为如下:
当时:
(8)
当时:
(9)
式中:θ是侧偏角;Cy为侧偏刚度;sy侧向滑移率。
2 跨座式单轨列车-轨道梁耦合系统动力学响应
2.1 曲线半径对轨道梁系统动态响应的影响
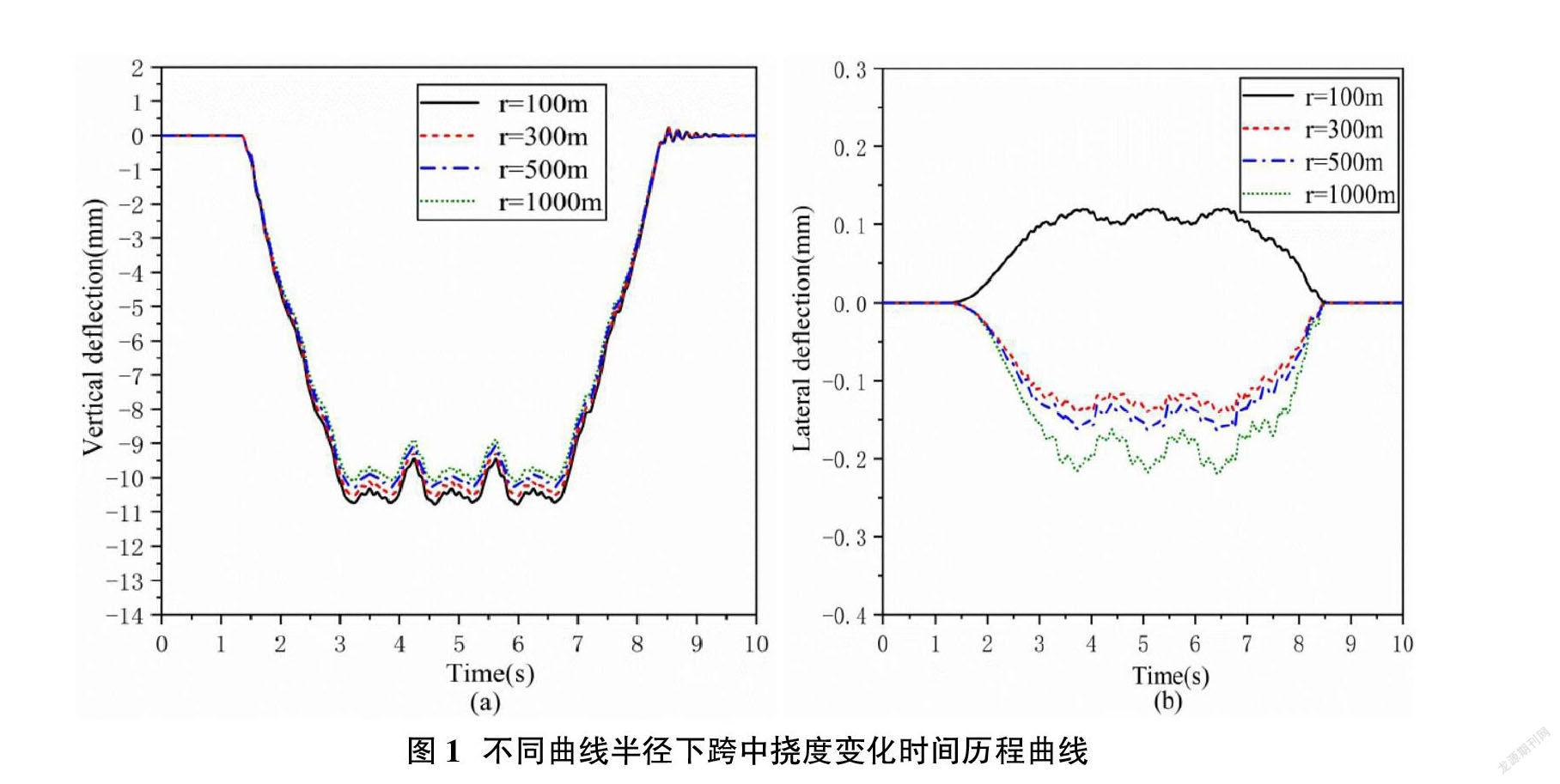
分析曲线半径在100~1000m范围内变化时对跨座式单轨车桥耦合系统振动响应的影响,仿真取车速40km/h,图1为轨道梁跨中竖、横挠度随曲率半径的变化曲线,由图1可知,轨道梁的垂向挠度随曲率半径的增加而减小,曲率半径为100m时其峰值为10.6mm,而横向挠度随曲率半径的增加而增加。
2.2 跨径和载重对轨道梁系统动态响应的影响
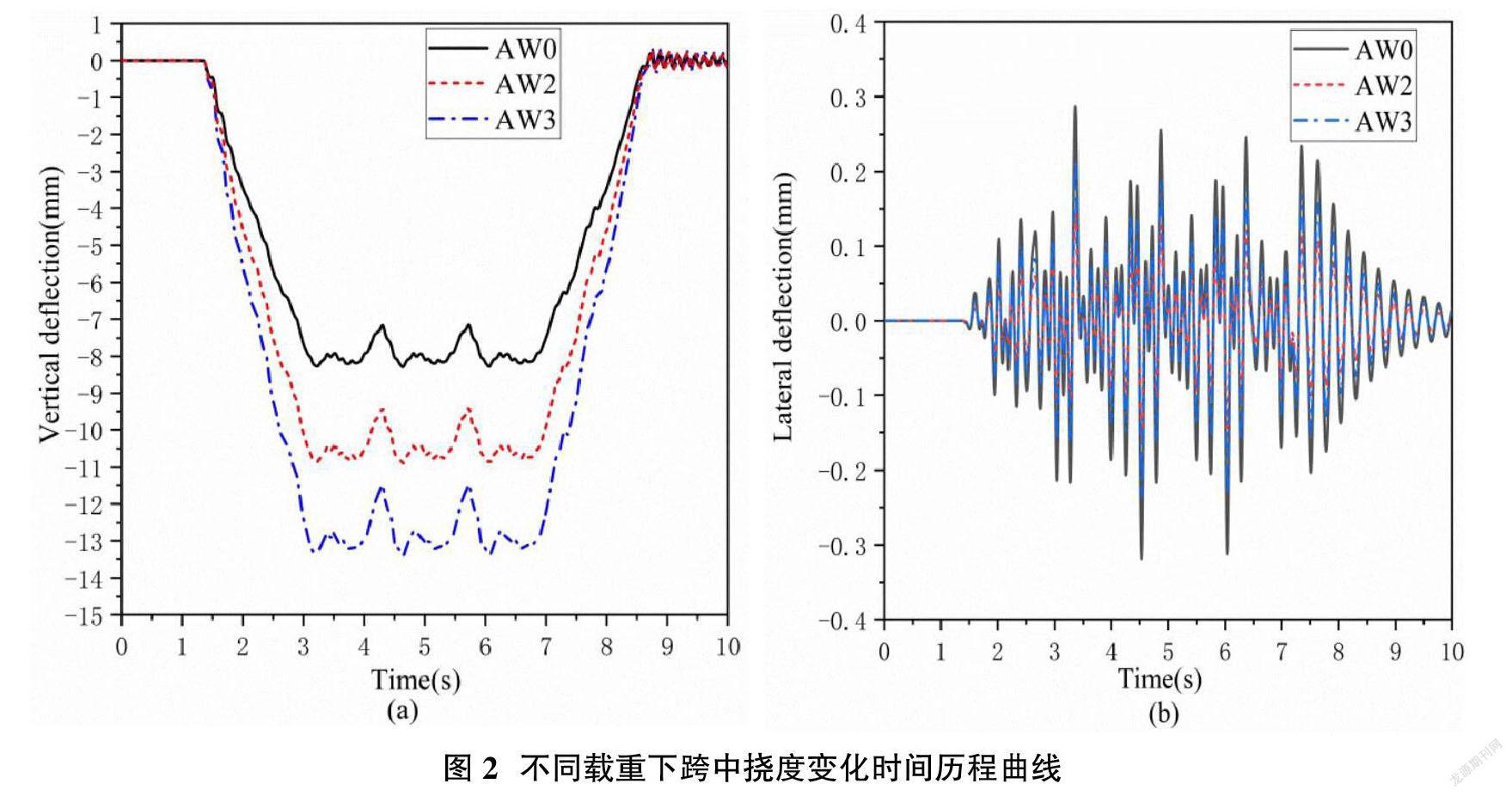
跨座式单轨交通轨道梁常见跨度一般在10-25m之间变化。因而,参数敏感性分析中,桥梁的跨度从10m逐渐增加到25m,考虑三种车辆荷载(空车(AW0)、定员(AW2)和满载(AW3))对轨道梁动态响应的影响。
图2为不同载荷下轨道梁跨中挠度时间历程曲线,由图2可知,随着载荷的增加,横竖向挠度均增大,车辆满载时,竖向和横向的最大挠度分别为13.2mm和0.32mm,车辆荷载对轨道梁有显着影响,跨距大于20m后急剧增加,轨道梁跨中横向挠度变化较为平缓;表明车辆超员状态为控制轨道梁竖向抗弯刚度设计的最不利状态。
3 结论
通过本文建立的跨座式单轨列车-轨道梁耦合动力学模型,研究不同轨道梁跨距和载客量工况对车辆系统响应的影响,结果表明:轨道梁跨中竖向位移和横向位移均随跨距的增加而增加,且跨中竖向位移变化幅度较大;跨中竖向位移随载客量的增大而增大,横向位移基本不受载重的影响。轨道梁的竖向加速度随跨径的增加先增后减,在跨距为18m左右出现拐点,峰值为0.84m/s2。
参考文献:
[1]GodaK, Nishigaito T, Hiraishi M, et al. A curving simulation for a monorail car[C]. Railroad Conference, 2000. Proceedings of the 2000 ASME/IEEE Joint. IEEE, 2000.
[2]Lee Chang Hun, Kim ChulWoo, KawataniM, et al. Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains[J]. Engineering Structures, 2005, 27(14): 1999-2013.
[3]C H. Lee, et al. Dynamic response of a monorail steel bridge under a moving train UJ], Journal ofsound & Vibration 294(2006), 562-579.
[4]Craig R. R. Jr. Bampton M. C.C. Coupling of Substructures for Dynamics Analyses]. ALAAJournal. 1968, 6(7): 1313-1319.