沉井基础竖向承载特性的离心模型试验研究

胡中波，马建林，徐 力，梅新咏，王钦科

(1.西南交通大学，成都 610031；2.中铁大桥勘测设计院集团有限公司，武汉 430056)



沉井基础竖向承载特性的离心模型试验研究

胡中波1，马建林1，徐 力2，梅新咏2，王钦科1

(1.西南交通大学，成都 610031；2.中铁大桥勘测设计院集团有限公司，武汉 430056)

基于离心模型试验对饱和砂土地基中沉井基础在竖向荷载作用下的承载特性进行研究，初步掌握地基极限承载力随基础埋深和基础宽度变化的规律，并对试验结果进行对比分析，结果表明：(1)基础埋深不大于5 m时，荷载-沉降曲线为陡降型，有明显的拐点出现，可取拐点对应的荷载作为极限承载力；基础埋深不小于10 m时，荷载-沉降曲线为缓变型，未出现明显的拐点，建议取相对沉降量(基础的实测沉降量与基础宽度的比值)对应的荷载作为极限承载力。(2)在均质地基环境中，极限承载力随基础相对埋深的增加近似呈指数型曲线增长。(3)进一步推求沉井基础极限承载力随基础宽度和相对埋深变化的函数表达式，其成果可用于估算砂土地基中沉井基础的地基极限承载力。

沉井基础;离心模型试验; 极限承载力; 基础埋深; 基础宽度

地基极限承载力的确定是工程实践中迫切需要解决的课题，大量的试验研究[1，2]表明，随着基础埋深的变化，地基土的破坏模式有着很大的不同，因此，深基础和浅基础承载力的评价形式是不同的。随着现代土木工程的发展，许多高层和超高层建筑、跨江和跨海大桥、高速铁路和高速公路等工程几乎都采用各种类型的桩基、沉井、沉箱、大型管柱等深基础形式，对于恰当评价深基础的地基承载力提出了紧迫的要求。

目前，用于计算地基极限承载力的方法主要有两种[3]。一是极限平衡理论法，即根据平衡方程和边界条件求得微分方程，求解此方程可得到地基土整体达到极限平衡时各点应力状态的解析解，以及相应最大剪切滑动破坏面的形状等。该方法理论严密，但计算过程相对繁琐，且只有个别简单情况才能得到解析解。二是极值法，亦称假定滑动面法，即人为假定地基土的剪切破裂面，结合相应的平衡和边界条件，求得土压力极值的破裂面便是所求的滑动面。然后假定在全部的滑动面上达到极限平衡，选取滑动面所包围的滑动体为脱离体，根据静力平衡条件求得极限荷载。该方法由于假定的滑动面不同往往会得到不同的经验公式。

关于深基础极限承载力的研究，至今已有不少观点，其中比较典型的有如下几种。

(1)太沙基公式[4，5]：认为基底的地基土体达到极限平衡时，分为3个区，滑动面与浅基础一致。这种假设与实际情况严重不符，但因运算简便而被广泛应用。

(2)汉森公式[6]：认为基底以上的土体按边载考虑，即只考虑基础边外土体的压重作用，而不考虑覆盖层的抗剪强度。该方法在基础埋深较浅时，计算精度较高。然而，随着基础埋深的增加，覆盖层的厚度逐渐加厚，由此部分土层的抗剪强度所承担的承载力逐渐增加，因而，该方法在基础埋深较深时，计算误差较大。

(3)梅耶霍夫公式[7，8]：认为塑性区从基底逐渐向上扩展，随着基础埋深的增加，滑裂面与基底水平面的夹角将会逐渐增大，最终尖灭在覆盖层中形成梨形的塑性区。该方法假定地基土为理想的刚塑性材料，未考虑塑性区内体积变化的影响，因而其应用受到一定的限制。

(4)别列赞捷夫公式[9]：针对砂土在密实状态下的承载力远超过以往的理论计算结果而提出的。认为在极限状态下，基础下形成剪切区，基础旁的土体形成压密区，根据这一假设条件下的平衡方程计算得到极限承载力。

(5)球孔扩张理论：球孔扩张理论自被提出后，便被广泛应用于解决静力触探、深基础承载力、沉桩及压密注浆等岩土工程问题[10-12]。在应用球孔扩张理论估算深基础的极限承载力时往往忽视了土在高应力环境下的破坏模式和非线性的强度特性，因而其应用受到一定的限制。

现有的理论已成功用于浅基础地基承载力的估算，但对于深厚而密实的砂性土地基承载力的估算却相差甚远，特别是对于平面尺寸、埋深均较大的沉井基础，其极限承载力计算尚未找到合适的方法，设计往往参考国内现行常用规范的计算公式，这些公式是在平板载荷试验的基础上建立的，试验中的平板最大尺寸不大于1 m2，埋深不超过6 m，公式中虽然考虑了地基土的深度修正和宽度修正，但实质上仍适用于浅基础情况[13]。

本文以土工离心模型试验为研究手段，开展了不同深度土层中沉井基础受力-沉降的模型试验，获取了不同深度、宽度条件下沉井基础在承载能力、沉降特性等方面的试验数据，探索了饱和砂土中沉井基础在竖向荷载作用下地基承载力随基础埋深和宽度的变化规律，为深层土体中沉井基础承载能力的确定提供试验支持。

1 试验方案

1.1 试验设备及装置

本次试验所使用的离心机为西南交通大学TLJ-2型土工离心机，其最大容量为100 gt，最大加速度为200g，有效半径为2.7 m。

试验所使用的模型箱底板及周围三面为钢板，正面为有机玻璃板，模型箱尺寸为80 cm(长)×70 cm(宽)×70 cm(高)。在离心模型试验中，受模型箱侧壁摩阻力的影响，试验的边界受力条件和变形条件往往会发生改变。对于地基承载力试验的基础底板，一般要求其宽度不超过模型箱最小边长的1/5[14，15]。本次试验制作了2种规格的沉井基础，其平面尺寸分别为10 cm(长)×7.5 cm(宽)和20 cm(长)×15 cm(宽)。采用的大沉井基础的宽度与模型箱最小边长的比值约为1/5，小沉井基础的宽度与模型箱最小边长的比值约为1/9，均满足试验要求，可忽略边界效应的影响。

1.2 地基土的制备与物理力学特性

试验土样选用细砂，平均粒径d50为0.329 mm，土粒比重为2.66，最大孔隙比为0.944，最小孔隙比为0.612。在离心模型试验中，由于基础和地基材料缩尺的不一致，往往存在粒径效应问题[16，17]，本次试验采用的大、小模型沉井基础的宽度与试验用砂平均粒径的比值分别为456和228，均满足试验要求，可忽略粒径效应对试验结果的影响。试验中砂土地基厚度为45 cm，分层摊铺，每层厚度为5 cm，根据每层的体积计算出每层砂土质量，使用室内轻型压实仪进行多遍夯击，直至砂土面达到设计高度。如此往复，试验土样全部填筑完成后，通过模型箱四角预埋的注水管缓慢从箱底向上注水，以避免扰动砂层或使砂层中有气泡存在；注入足够水量，以水面高于土面1 cm为宜，终止注水，静置24 h，使砂土在自重作用下压密，以保证每次试验土样的均一性。试验土样基本参数见表1。

表1 试验土样基本参数

1.3 试验加载及量测

图1 试验布置示意(单位：cm)

图3 荷载-沉降关系曲线

试验采用自主设计加工的加载装置施加竖向载荷，如图1所示。试验中每0.5 kN施加一级荷载，荷载施加结束后，观察测力传感器读数的大小，待读数稳定后，记录下稳定读数，施加下一级荷载，以此类推，直至加载至某级荷载时，测力传感器读数不能稳定或小于上一级稳定读数，停止加载，终止试验。

试验采用中国工程物理研究院研发的TY202型土压力盒量测基底及周围土体的土压力，采用CW50型差动式位移传感器测量沉井及周围土体的沉降量，传感器外形如图2所示。

图2 传感器外形

1.4 试验安排

本文针对饱和砂土地基开展了8组土工离心模型试验，其中模型沉井包括大、小两组，每组模型各开展埋深为0、5、10 cm和15 cm 4组试验，具体试验安排如表2所示。

表2 模型试验安排

2 试验结果分析

2.1 荷载-沉降关系曲线

据上述试验条件，按照N=100的模型比放大后，得到小、大原型沉井在不同埋深条件下的荷载-沉降曲线如图3所示。图中横坐标为原型沉井上部施加的荷载，MN；纵坐标S/B(原型沉井的实测沉降量与基础宽度的比值)为归一化后基础的相对沉降量。

由图3可知：(1)荷载-沉降曲线初始阶段，近似为直线，且斜率较小，随着基础埋深的增加，斜率呈减小趋势；(2)基础埋深较浅(0、5 m)时，荷载-沉降曲线为陡降型，当S/B达到0.075左右时，荷载-沉降曲线经过一个明显的拐点，拐点之后，沉降急剧增加；(3)基础埋深较深(10、15 m)时，荷载-沉降曲线为缓变型，当S/B达到0.075左右时，荷载-沉降曲线经过一个不是很明显的拐点，进入另一近似的直线段，且这一阶段斜率较前一阶段大。

上述规律说明随着基础埋深的增加，地基的破坏形式从整体剪切破坏逐渐过渡到局部剪切破坏或冲切剪切破坏。

2.2 极限承载力的确定

原型沉井在不同埋深条件下，随着上部荷载的增加，沉降呈非线性变化，基础埋深不大于5 m时，荷载-沉降曲线有明显的拐点，取拐点对应的荷载为极限承载力。基础埋深不小于10 m时，荷载-沉降曲线的拐点不明显，取斜率不同的两阶段直线段的交点对应的荷载为极限承载力。

根据以上原则，得到不同原型沉井在不同深宽比(H/B)条件下的极限承载力、对应的基础相对沉降量(S/B)、与零埋深比极限承载力增大程度的汇总结果如表3、表4所示。

由表3可知，基础宽度、埋深对地基极限承载力的结果影响显著。当基础宽度B=7.5 m时，不同埋深条件下得到的地基土的极限承载力分别为101.08、120.01、143.28 MN和194.34 MN；对应的基础相对沉降分别为0.064、0.067、0.074和0.075，总体上呈增大趋势，其均值为0.07与零埋深相比，随着基础埋深的增加，极限承载力分别提高了18.73%、41.75%和92.26%。

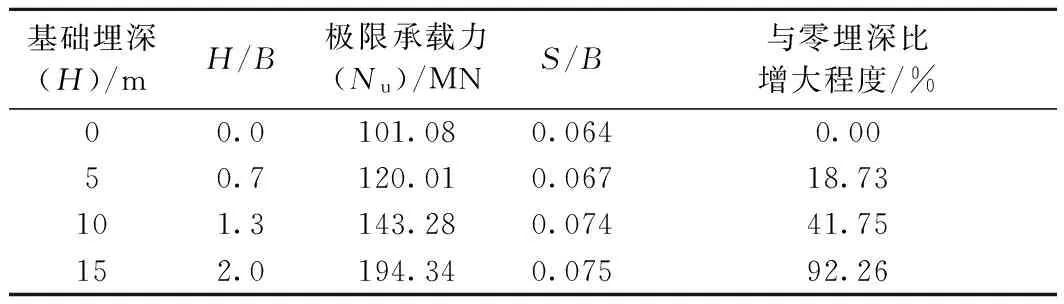
表3 极限承载力试验结果(小沉井)

表4 极限承载力试验结果(大沉井)

由表4可知，基础宽度、埋深对地基极限承载力的结果影响显著。当基础宽度B=15 m时，不同埋深条件下得到的地基土的极限承载力分别为448.92、561.77、812.24 MN和956.52 MN；对应的基础相对沉降分别为0.073、0.075、0.096和0.092，总体上呈增大趋势，其均值为0.08。与零埋深相比，随着基础埋深的增加，极限承载力分别提高了25.14%、80.93%和113.07%。

2.3 极限承载力随基础埋深的变化规律

由前述分析可知，随着基础埋置深度的增加，地基土的极限承载力得到了显著的提高，地基的破坏形式从整体剪切破坏过渡到局部剪切或冲切剪切破坏。地基土的极限承载力与基础相对埋深(H/B)的关系如图4所示。

图4 极限承载力与基础相对埋深关系

由图4可知，极限承载力随基础相对埋深的增加近似呈指数型曲线增长。对试验结果进行曲线拟合(如图4中的实线所示)，拟合结果如表5所示。

2.4 极限承载力计算模型的建立

由前述拟合结果可知，当基础宽度确定时，地基土的极限承载力与基础的相对埋深呈指数函数关系，可用如下形式的表达式表示

表5 指数型曲线拟合结果

式中，Nu为基础不同相对埋深对应的极限承载力，MN；h为基础的相对埋深，h=H/B，其中H为基础埋深，B为基础宽度；y0、A、R0为拟合参数，与土层性质、基础埋深、宽度等因素有关。

由式(1)可知，极限承载力与基础相对埋深的计算模型是非线性模型，难以直接求解。考虑到模型试验的地基土为均质土，土层性质相同，因而可忽略土层性质对拟合参数的影响。基于现有的离心模型试验结果，并假定拟合参数随基础宽度线性变化，分别对拟合参数进行线性拟合，得到的拟合结果如下。

(1)拟合参数y0与基础宽度B的关系

(2)拟合参数A与基础宽度B的关系

(3)拟合参数R0与基础宽度B的关系

将式(2)～式(4)代入式(1)中，得到极限承载力与基础宽度和相对埋深的关系为

Nu=-232.08+41.99B-

式中，Nu为沉井基础的极限承载力，MN；B为基础的宽度，m；h为基础的相对埋深，h=H/B，其中H为基础的埋深，m。

式(5)是基于现有的离心模型试验结果推求的，试验中由于基础宽度组数较少(只有2组)，拟合参数y0、A、R0与基础宽度间假定满足线性分布，其准确性有待进一步检验。

3 结论与建议

本文采用具有多功能控制平台、先进操控系统、数据自动化采集系统的TLJ-2型土工离心机，进行了多组饱和砂土地基环境中沉井基础极限承载力的离心模型试验。对比研究了基础尺寸、埋深等因素对极限承载力的影响。通过试验结果的对比分析，得到如下结论。

(1)基础埋深不大于5 m时，荷载-沉降曲线为陡降型，有明显的拐点出现；基础埋深不小于10 m时，荷载-沉降曲线为缓变型，未出现明显的拐点，说明随着基础埋深的增加，地基的破坏形式从整体剪切破坏逐渐过渡到局部剪切破坏或冲切剪切破坏。

(2)基于本文的试验结果，当荷载-沉降曲线有拐点时，取拐点处对应的荷载为极限承载力；当荷载-沉降曲线未出现明显的拐点时，建议取基础的相对沉降值S/B=0.07～0.08对应的荷载作为极限承载力。

(3)在均质地基环境中，基础埋深、宽度对极限承载力的提高影响显著，极限承载力随基础相对埋深的增加近似呈指数型曲线增长。

(4)基于离心模型试验结果推求了沉井基础极限承载力随基础宽度和相对埋深变化的函数表达式，其成果可用于估算砂土环境中沉井基础的极限承载力。

[1] 殷万寿.深水基础工程[M].2版.北京：中国铁道出版社，2003.

[2] 史佩栋.深基础工程特殊技术问题[M].北京:人民交通出版社，2006.

[3] 郑大同.地基极限承载力的计算[M].北京:中国建筑工业出版社，1979.

[4] Terzaghi K. Theoretical Soil Mechanics[M]. John Wiley， 1943.

[5] Terzaghi K， Peck R B. Soil mechanics in engineering practice[M]. 2nd Edition. John Wiley， 1967.

[6] Hansen J B. A revised and extended formula for bearing capacity. Danish Geotechnical Institute Bulletin， 1970(28):5-11.

[7] Meyerhof G G. Influence of roughness of base and ground-water conditions on the ultimate bearing capacity of foundations[J]. Geotechnique， 1955，5(3):227-242.

[8] Meyerhof G G. The ultimate bearing of wedge-shaped foundations[C]∥Proceedings of the 5th International Conference on Soil Mechanics， London， 1961:105-123.

[9] Berezantsev V C， Khristoforov V， Golubkov V. Load-bearing capacity and deformation of piled foundations[C]∥Proceedings of the 5th International Conference on Soil Mechanics， London， 1961:11-27.

[10]贾尚华，赵春风，赵程.砂土中柱孔扩张问题的扩孔压力与扩孔半径分析[J].岩石力学与工程学报，2015，34(1):182-188.

[11]李镜培，李林，孙德安，等.饱和软土地层静压沉桩阻力理论研究[J].岩土工程学报，2015，37(8):1454-1461.

[12]周航，孔纲强，刘汉龙.基于圆孔扩张理论的静压楔形桩沉桩挤土效应研究[J].中国公路学报，2014，27(4):24-30.

[13]阮静，胡丰.泰州大桥中塔沉井基础承载力模型试验研究[J].中国工程科学，2012，14(5):57-61.

[14]柳飞，李东海，吴炼石.侧摩阻力对桩基粒径效应的影响研究[J].岩土工程学报，2013，35(S2):1016-1019.

[15]Kusakabe O， Kimura T， Saitoh K. Geotechnical model tests of bearing capacity problems in a centrifuge[J]. Geotechnique. 1985，35(1):33-45.

[16]徐光明，章为民.离心模型中的粒径效应和边界效应研究[J].岩土工程学报，1996，18(3):80-86.

[17]王年香，章为民.土工离心模型试验技术与应用[M].北京:中国建筑工业出版社，2015.

Centrifugal Model Test on Vertical Bearing Properties of Open Caisson Foundation

HU Zhong-bo1， MA Jian-lin1， XU Li2， MEI Xin-yong2， WANG Qin-ke1

(1.Southwest Jiaotong University， Chengdu 610031， China; 2.China Railway Major Bridge Reconnaissance & Design Group Co.， Ltd.， Wuhan 430056， China)

Based on centrifuge model test， the bearing properties of open caisson foundation in saturated sand under vertical load are studied， the variation law of the ultimate bearing capacity of soil with the change of the embedded depth and foundation are identified， and contrastive analysis of the test results are conducted. The results show that (1) when the embedded depth of foundation is less than 5 meters， the curve shape of load-settlement is steep and there is a clear inflection point and the desirable inflection point corresponding to the load is the ultimate bearing capacity; when the embedded depth of foundation is not less than 10 meters， the curve shape of load-settlement is flat and no clear inflection point showed in the curve， and it is suggested the loading with relative settlementS/B=0.07 ～ 0.08 be regarded as the ultimate bearing capacity; (2) in homogeneous foundation， the ultimate bearing capacity increases exponentially with the increase of the relative embedded depth of foundation; (3) the expression function on the ultimate bearing capacity of open caisson foundation is further derived in view of the influence of the relative depth and foundation width， which can be used to estimate the ultimate bearing capacity of the open caisson foundation in sand soil．

Open caisson foundation; Centrifugal model test; Ultimate bearing capacity; Foundation depth; Foundation width

2016-05-12；

2016-06-13

中国铁路总公司科技研究开发计划(2013G001-A-2)

胡中波(1987—)，男，工程师，2016年毕业于西南交通大学，工学博士，E-mail：huzhongbo87@163.com。

1004-2954(2016)12-0080-05

TU473.2

A

10.13238/j.issn.1004-2954.2016.12.018