复杂问题简单化
2016-12-28□刘笑
数学小灵通·3-4年级 2016年9期
□刘 笑
复杂问题简单化
□刘 笑
小朋友,在做图形找规律的题目时,我们可以从简单的情况出发,逐个图形分析,找出图形之间的关系,从而找出规律。
同一个平面内画2016条直线,最多可以有多少个不同的交点?
我是这样解的。
要将2016条直线在同一个平面内画出来,几乎是不可能的,因此我们不妨将题目中的条件“化大为小”,从简单的问题入手开始操作分析。
显然,两条直线只有1个交点。
当同一个平面内有3条直线时(如图1),当第三条直线与前2条直线分别相交时交点个数最多,最多交点个数为1+2=3(个)。

图1
当同一个平面内有4条直线时(如图2),只有当第4条直线与前3条直线分别相交时,交点个数也才能达到最多,最多交点个数为1+2+3=6(个)。
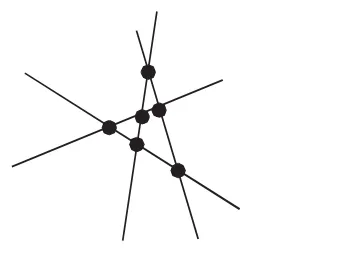
图2
同样的道理,当同一个平面内有5条直线时(如图3),只有当第5条直线与前4条直线分别相交时,交点个数才能达到最多,最多交点个数为1+2+3+4=10(个)。
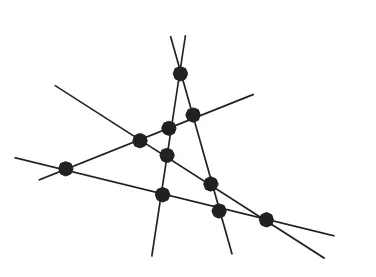
图3
依此类推,同一个平面内的2016条直线,最多的交点个数为1+2+3+4+…+2015=(1+2015)×2015÷2=2031120(个)。
(作者单位:江苏省海门市德胜小学)
