创新设问方式，引导备考方向——以南通通州两道九年级期中考题为例

☉江苏省南通市通州湾海晏中学 姜海平

创新设问方式，引导备考方向
——以南通通州两道九年级期中考题为例

☉江苏省南通市通州湾海晏中学 姜海平

我们知道，最近两年来北京中考数学卷在最后几道把关题上不断创新，一改长期以来“八股化”的试题呈现形式，一方面，加大开放题考查的力度.另一方面，坚持用新定义考题引导中考命题改革，着力培养学生的创新精神.这种更为“现实引领”（相比一些文件，甚或“课标”），使得北京市各区、各校在平时的阶段检测、期中、期末试卷中都出现了大量优秀的考题，所以北京各区的试卷也成为全国各地有命题兴趣的研究者关注的重点，也悄然影响着不少地区.巧合的是，我们发现不但北京有通州区，在江苏南通也有一个通州区，最近我们注意到该地区九年级期中试卷竟然也与北京中考倡导的开放考查、新定义考查高度类似，本文选取该卷中的两道考题，赏析试题并跟进思考，提供研讨.

一、两道九年级考题的解法与赏析

考题1（2016年11月南通通州区九年级期中卷，第26题）如图1，△ABC中，AC=BC，∠ACB=90°，将边AC绕点A逆时针旋转θ（0°＜θ＜90°）得线段AP，作点B关于直线CP得对称点Q，连接AQ，BQ.

（1）求∠AQB的度数；

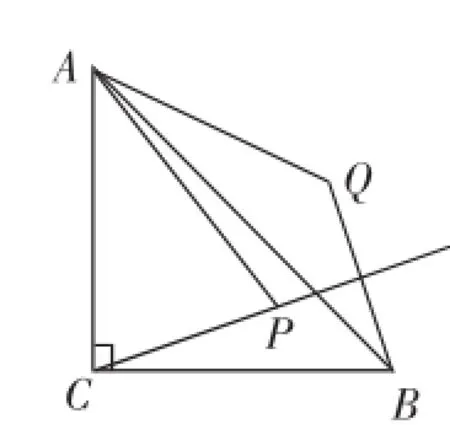
图1

图2

思路简述：（1）如图2，连接CQ.由题意可知，CB=CQ= CA.则∠BQC=90°-∠BCQ，∠AQC=90°-∠ACQ.

（2）求解思路如下：

①过点A作AE⊥BQ，交BQ的延长线于点E，如图2所示；

④由B，Q两点关于直线CP对称，AC=AP，可求∠PCQ=15°，∠ACP=75°；

⑤从而求出θ=30°.（或者写成：从而求出θ的度数）

解后反思：第（1）问解出∠AQB是定值135°，则该问题应该有一个深层结构，这就是如图3这样的两个圆，其实是分别以A、C为圆心的两个等圆，点P在以A为圆心、AC为半径的圆上，而点Q在以C为圆心、CA为半径的圆上！理由容易理解，前者AP=AC；后者有CA=CB=CQ.这样的话，就容易理解∠AQB为定值的原因了，当点Q在劣弧AB上时，∠AQB一定是钝角135°；而去除考题中的限制条件旋转θ（0°＜θ＜90°）后，则Q还可能在优弧AB上，此时∠AQB就为45°！

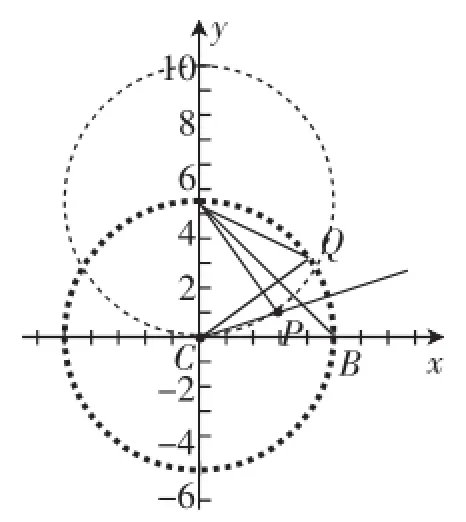
图3

第（2）问的关键在于对几个特殊数据、角度的敏感上，及时构造、利用特殊直角三角形，就可迅速确定转化方向，发现△ACQ为等边三角形是最关键的一步！

考题2（2016年11月南通通州区九年级期中卷，第28题）定义：如图4，对于线段AB及线段AB外一点C，称∠ACB为点C对线段AB的张角，记作∠（C，AB）.

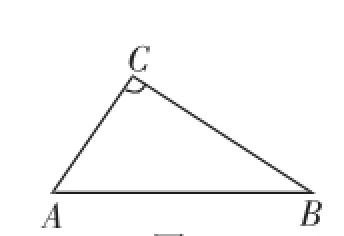
图4

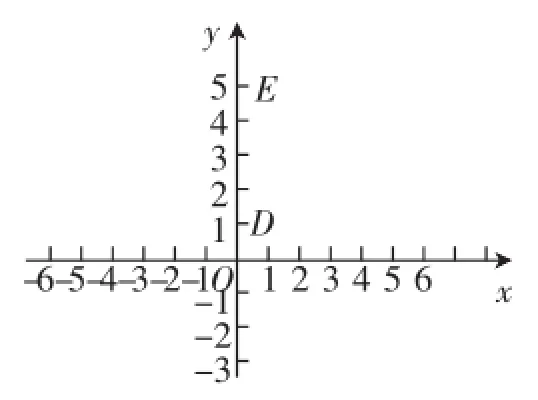
图5

如图5，在平面直角坐标系xOy中，点D（0，1），E（0，5），F是该坐标系内的一个动点.

（1）若∠（F，DE）=30°，则满足条件的点F有_____个；

（2）若点F在x轴正半轴上，且∠（F，DE）=30°，求点F的坐标；

（3）当点F在x轴上移动时，∠（F，DE）是否有最大值？若有，求点F的坐标，并说明最大的理由；若没有，请说明理由.

思路简述：（1）解题的关键是想清楚新定义中的点F的轨迹，即点F应该在一个圆上，该圆经过D，E，F三点，则弦DE所对的圆周角就是符合要求的，故点F有无数个；这里可构造一个草图示意，如图6，先作等边△DEP，则以P为圆心，PE为半径的圆P上的一些点，比如优弧DFE上（端点D，E除外）就是F的位置；当然，根据对称性，点P还可以在第二象限.

图6

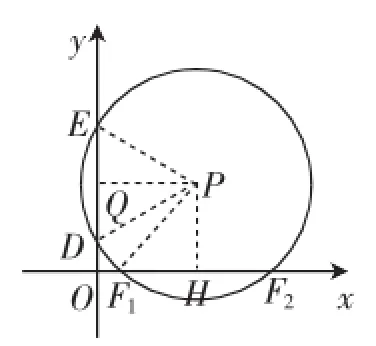
图7

（2）如图6，由（1）知，点F在⊙P上，且圆心角∠DPE= 60°，再将思路转化到图7中，当F点在x轴正半轴上时，一共有2个点，分别是F1、F2.过点P分别向x轴、y轴作垂线，垂足分别为H和Q，在Rt△PDQ中，PD=DE=4，∠PDQ= 60°，则PD=2，PQ=.由辅助线作法可知四边形PHOQ为矩形，则OH=PQ=，PH=OQ=3.在Rt△PHF1中，由勾股定理可知，，所以OF1=同理，所以点F的坐标为，0）或

（3）当过点D，E的⊙P与x轴相切于点F时，∠（F，DE）最大，如图8，⊙P与x轴正半轴相切于点F，连接PD，PF，作PQ垂直于y轴，垂足为Q，则PF=OQ=3，即⊙P的半径为3，得PQ=，所以F .

图8

根据对称性质，关于y轴对称还有一种情形，当点F在x轴负半轴上时，可得.

∠（F，DE）最大的理由是：在x轴正半轴上任取一点M（不与点F重合），连接MD，ME，ME交⊙P于点N，连接ND，则∠DFE=∠DNE.因为∠DNE是△DMN的外角，所以∠DNE>∠DME，所以∠DFE>∠DME，即此时∠（F，DE）最大.

若切点F在x轴的负半轴上，同理可证得∠DFE>∠DME.

解后反思：第（1）问虽然简单，只要填写一个“无数”就能得分，但是想清楚这个“无数”个点F的轨迹，一段圆弧却对于后续问题的求解起到奠基、全局作用.

第（2）问在上一问的基础上，限制和强化了点F的位置，即既要在圆P上，又要出现在x轴正半轴上，这样就是x正半轴与圆P的两个交点了！

第（3）问比较抽象，需要想象出经过点D，E的圆与x轴相切的情形，切点恰为满足题意的F点.

二、进一步的思考

1.地区命题责任重大，引导教学和备考方向

作为一个地区的命题来说，往往几千人的全样本参与限时测试，其影响面之广、之深是一节所谓的公开课、示范课或写一篇案例文章所不能及的，故承担地区命题工作使命光荣，责任重大，既要科学准确诊断、评估学生前一阶段学习情况，又要对后一阶段的教学和备考方向进行有效引领.比如上文中两道考题，不仅考查了学生对旋转、圆的相关知识的考查，而且导向着引导学生自主发现几何图形中蕴含的几何结构，促进深入思考、洞察问题深层结构的能力，当然，这些都是需要教师本人首先要成为命题者的知音，自身先达到对考题的深刻理解，才能将这种反思和发现结构的能力传递给学生.

2.重视开放考题设计，创新考题设问的方式

考题1的第（2）问学习和借鉴了北京卷几何把关题的考查方式，只要求学生展示思路，而不需要拘泥于具体的解题细节，这种开放式的解答要求鼓励学生不同的思路，节约了书写规范语句的时间，使得这一小问的考查目的得到强化，而不需要学生展示细枝末节，对于阅卷、评分也提出了较高的要求，阅卷老师需要仔细辨析学生的思路、解题路径是否有效，能否贯通思路，相比其他试题直接比对标准解答的评分来说，难度增大很多.

三、结束语

坦率地说，限于笔者的搜集和能力所及，现如今很难在一份期中试卷中看出如此的精彩和用心，这样的试题并不是简单的拼凑行为，而是苦心经营和立意引领，相信该地区的师生深入挖掘、深刻理解考题，一定能从中悟出下一阶段的学习与备考方向，而不是把精力都放在一些不符合本地区命题风格的繁杂习题上，甚至是一些不能体现数学本质的试题.也期待更多的承担命题任务的老师能设计出更多这样的“好的题目”.

1.刘东升.一次期中考试阅卷随笔［J］.中学数学教学参考（中），2016（1-2）.

2.夏盛亮.引导回归教材，倡导开放取向——一次县级期末卷的命题取向分析［J］.中学数学（下），2014（1）.

3.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

4.付小飞.明辨并列与递进，引导分离和聚焦——2016年江苏苏州中考第28题解析与教学思考［J］.中学数学（下），2016（7）.

5.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.H