小网格大奥秘——2016年天津市中考试题第18题第（Ⅱ）小题的思考

☉天津市实验中学 刘 涛

小网格大奥秘
——2016年天津市中考试题第18题第（Ⅱ）小题的思考

☉天津市实验中学 刘 涛

2016年天津市中考试题第18题第（Ⅱ）小题，以网格为载体，借助无刻度的直尺，在《义务教育数学课程标准（2011年版）》中对作图的要求统领下，既考查了学生利用网格，综合运用数学知识解决问题的能力，又锻炼了学生理解数学语言并有效运用数学语言进行精准表述的能力，具有较高的思维含量，对提升学生的思维能力和表达能力大有裨益.

一、试题呈现

题目如图1，在每个小正方形的边长为1的网格中，A，E为格点，B，F为小正方形边的中点，C为AE，BF的延长线的交点.

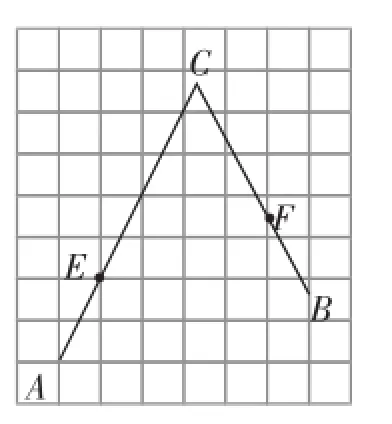
图1

（Ⅰ）AE的长等于_____；

（Ⅱ）若点P在线段AC上，点Q在线段BC上，且满足AP=PQ=QB，请在如图1所示的网格中，用无刻度的直尺，画出线段PQ，并简要说明点P，Q的位置是如何找到的（不要求证明）.

二、思路探究

关于第（Ⅱ）问的画法是从何而来的呢？

如图2，以A为坐标原点，点A所在的横网格线为x轴和y轴，建立平面直角坐标系，可得点A（0，0）、B

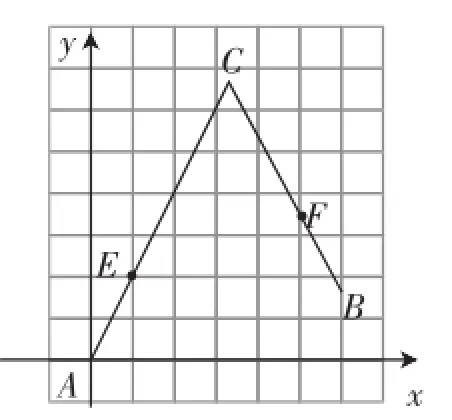
图2

由条件“点P在线段AC上，点Q在线段BC上”，可设点P（m，2m），Q

由条件“满足AP=PQ=QB”，可得：

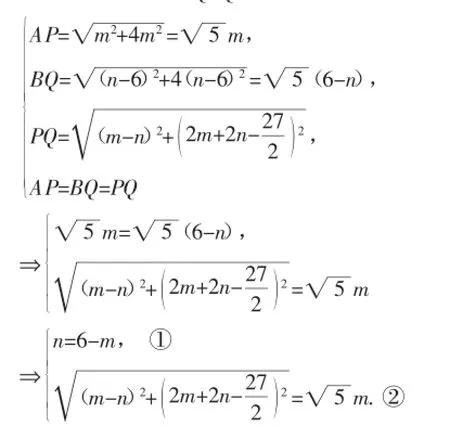
所以，很容易确定线段AC与横网格线的交点即为点P.

对于点Q位置可以从以下两个角度进行分析：

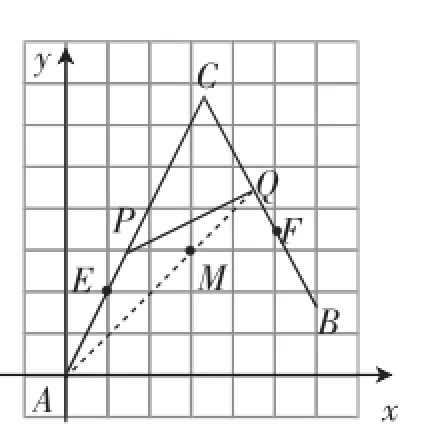
图3

本题通过建立适当的平面直角坐标系，根据要求作出的点所满足的等量关系建立方程，先求出点的坐标再进行网格中定位.这种解析法的求解过程清晰流畅，求解方法自然生成！

三、思路再探

参考答案是从“数”的角度求解的，能否从“形”的角度探究P、Q两点的位置呢？

探究：首先，我们假设P、Q两点的位置已经在线段AC、BC上确定下来了，由条件AP=PQ=QB，可构造如图4所示的全等的直角三角形.

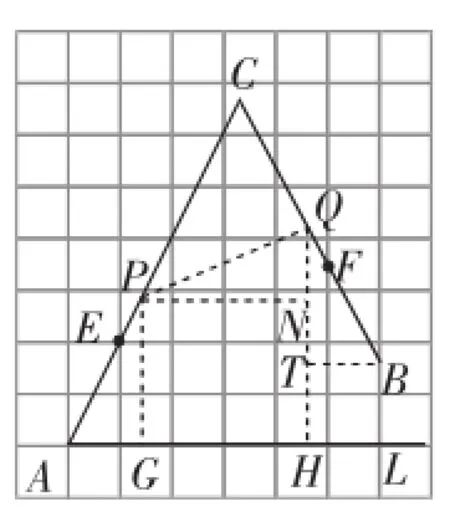
图4

具体做法如下：假设P、Q两点已作出，过P、Q两点分别作PG⊥AL于点G，QH⊥AL于点H，过点P作PN⊥QH于点N，再过点B作BT⊥QH于点H.

由AP=PQ=QB，得EP=FQ.

由tan∠CAG=tan∠CBT=2，则AG=BT=1+t，PG=QT= 2+2t，从而得PN=GH=6-2（1+t）=4-2t，QN=HT=.

在Rt△PQN中，由勾股定理PN2+QN2=PQ2，得（4-2t）2+，整理得4t2+104t-53=0，因式分解得（2t-1）（2t+53）=0，解得t1=，t2=-（舍）.

下面是P、Q两点位置的确定方法：

先考虑点P的确定方法：

①线段AC与网格线相交，得点P；（如参考答案做法）

②取格点M、N，连接MN与AC相交，得点P；（或者是以要求的点P为矩形对角线交点的做法均可，但是要注意在作法中一定要写“与AC相交，得点P”）（如图5）

③取格点H、I，连接HI与网格线相交，得点D，取格点J、K，连接JK与网格线相交，得点G，连接DG与AC相交，得点P；（如图5）

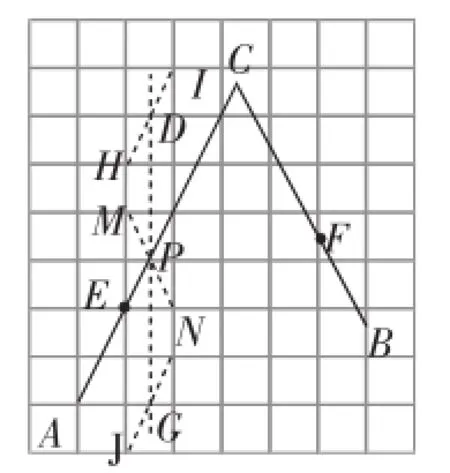
图5

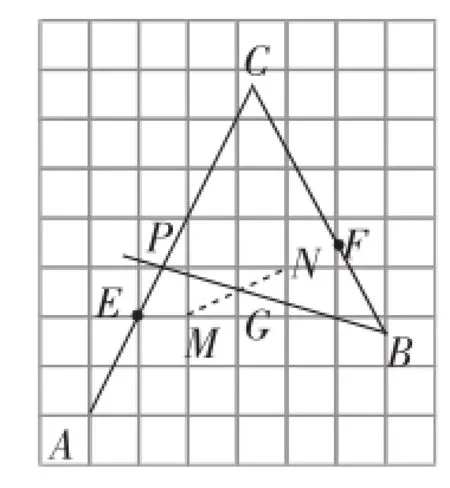
图6

④取格点M、N，连接MN与网格线交于点G，连接BG并延长，交AC于点P.（如图6）

再考虑点Q的确定方法：

①取格点M（3，3）或其他格点M（t，t），作直线AM与BC相交，得点Q；（如参考答案做法）

②取格点M、N，连接MN与BC相交，得点Q；（或者是以上述MN为对角线的小正方形所在的奇数个矩形的对角线与BC相交，均可得点Q）；（如图7）

图7

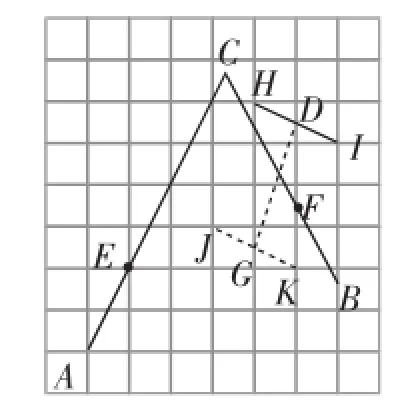
图8

③取格点H、I，连接HI与网格线相交，得点D，取格点J、K，连接JK与网格线相交，得点G，连接DG与BC相交，得点Q（下面两种做法均采用这种叙述过程）.（如图8）继续深入分析图形的性质，如图9，可得PN=PG=QT=3.

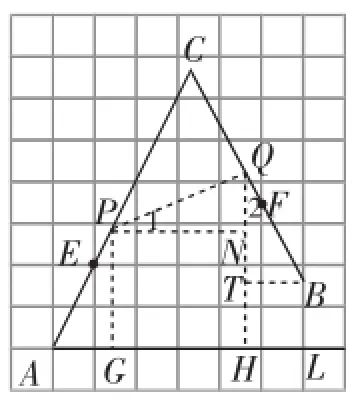
图9

又AP=PQ=QB，∠AGP=∠PNQ=∠BTQ=90°，所以△AGP≌△PNQ≌△BTQ.所以∠1=∠2.

进而得到∠PQB=90°，即PQ⊥BC.

这样一来，点Q便有了新的确定方法：

①取格点G、H，连接GH与网格线交于点D，连接PD交BC于点Q；（如图10）

（Ⅱ）由t=

图10

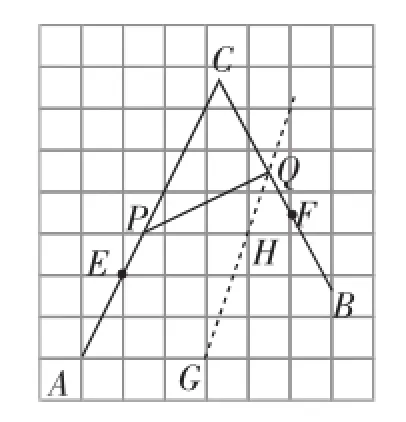
图11

②取格点G、H，连接GH并延长交BC于点Q（如图11）.（这里若连接PG、BG，则四边形BGPQ是正方形）

结合前面的解析法和构造法，我们可以一次性地确定P、Q两点的位置.

①取格点G、H、M、N，连接GH与网格线交于点D，连接MN与网格线交于点O，连接DO并延长分别交BC于点Q，交AC于点P，线段PQ即为所求；（如图12）

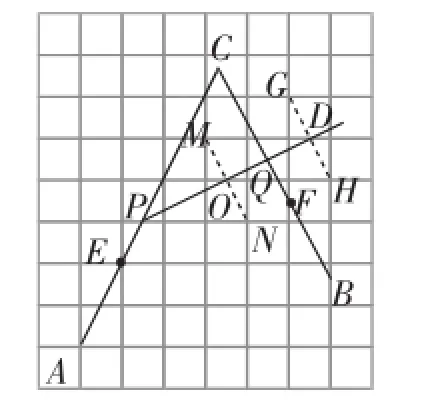
图12

图13

②取格点G、H、S、T，连接GH与网格线交于点D，连接ST与网格线交于点K，连接DO分别交BC于点Q，交AC于点P，线段PQ即为所求.（如图13）

四、数学语言的准确理解和表述

本题在审题环节特别要注意对“如何找到”四个字的理解，这将直接影响我们的数学语言是否到位，是否精准的问题，因此这一点很是关键.本题要寻求的是“点”，那我们就要清楚这一事实：点，不是单摆浮搁的，它必须以线作为载体来呈现，所以本题中的“如何找到”的意思应该理解为“哪两条直线相交得点P，哪两条直线相交得点Q”，又已知点P在线段AC上，点Q在线段BC上，那么在表述中一定要有“与AC相交”、“与BC相交”的说法.

以下就是学生在中考中出现的作法写得不规范，或者有科学性错误的地方：

①取格点P（点P不是格点）；

②点P的找法中的第二种方法错误地说成“取格点M、N，连接MN与网格线相交于点P”，出现了没有在AC上交出点P的错误作法，也就是说，即使这个点确实在AC上，也要直接进行说明；

③连接线段并延长要看清楚方向，最好就说成“作直线”，避免产生科学性错误；

④选取点时尽量不要用平移来叙述，若是从格点平移至格点还可以，若不是格点就有问题了，因为这样的平移不具有可操作性，再有平移点是不能说“与直线交于某点”的，因为点平移后还是点，它与直线只有“在直线上”或者“在直线外”两种位置关系，不能用“相交”来描述.

五、回顾反思

以网格为背景的探究性问题，使得图形问题充满趣味又不失数学味道，简简单单的“小”网格，在数学知识的统领下，指引着我们不断地去探寻其中的“大”奥秘.解析法——网格建系，先算后画，生成自然；构造法——几何直观，方法众多，精彩纷呈.若能将两种方法综合运用，必定珠联璧合，相得益彰，焕发出更为绚烂夺目的光彩.希望我们能在面对网格的问题中都能做到“四精”（即作图精致；语言精准；技法精湛；思维精密），不断前行，探寻“小”网格中更“大”的奥秘.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.沈德辉，顾洪敏.知其源得其法：2014年天津市中考数学第18题第（2）小题的思考［J］.中国数学教育（初中版），2015（3）.

3.白丽娜，刘金英，顾洪敏.探索网格作图问题提升数学思维能力：2015年天津市中考试题第18题第（2）小题的思考［J］.中国数学教育（初中版），2016（7/8）.H