核心素养下的初中数学教学初探

☉江苏省海门市东洲国际学校 夏冬平

核心素养下的初中数学教学初探

☉江苏省海门市东洲国际学校 夏冬平

核心素养是个人终身发展、融入主流社会和充分就业所必需的素养的集合.《中国学生发展核心素养（征求意见稿）》中提出了九大核心素养，就是为了确保学生在校所学的技能能够充分满足后续大学深造或社会就业的需求，成为21世纪称职的社会公民、员工及领导者.

当前，教育正从“知识核心时代”走向“核心素养时代”，核心素养必然会引领、辐射数学课堂教学，彰显数学教学的育人价值，使之自觉为人的终身发展服务.教师要变教学视角为教育视角，突破传统的知识视野、课堂视野，走进学生的生活，走进学生的心田，创造适合学生丰富成长的教育.初中数学教学要实现三个转向，通过一系列的尝试，以期培养孩子适应未来社会的关键能力和必备品格.

一、由“知识传授”转向“合适情境”

数学学科的特质就是逻辑性和严密性强，似乎所学的知识在我们以后的工作和生活中很少用到.学生往往是死记公式、定理，只要掌握解题技能、考试得高分就可以了，而缺乏用数学的眼光去观察、决策身边事物的能力.这就要求我们的教师把“抽象的数学知识”转向“合适情境”，让学生在合适的具体情境中掌握知识，利用掌握的知识解决实际问题，让学生感觉“数学源于现实，寓于现实，用于现实”，而不是高不可攀或无所是处的.

以“二次函数的图像和性质”中的喷泉问题为例.按照传统教学，教师建立适当的直角坐标系，指导学生寻找到（或者自己给出）相应的条件，然后按照要求设出解析式，代入数据，求解完成.在传统教学过程中这个问题就是一个“枯燥”的二次函数问题，学生非常感兴趣的一个实际问题，就这样变成了“被扒光”了的“赤裸裸”的二次函数解析式求法的变式问题，把本题内部蕴含的解决问题的能力扼杀了.

在教学中，我重新设计了如下的提问：

（1）喷泉的路线可以看成什么样的函数图像？

（2）图像有没有最高（低）点？

（3）怎样来建立适当的直角坐标系来表示这个顶点和喷泉的水的落点坐标？

（4）选择一般式还是顶点式来求这个函数的解析式？

（5）如何求出水口的高度？

在这个过程中，学生从发现问题、分析问题、寻找解法，到最后解决问题，完全是在“合适的情景”中进行的.

二、由“数学知识”转向“数学素养”

全国中小学整体改革专业委员会理事长傅国亮认为：“核心素养强调的不是知识和技能，而是获取知识的能力.核心素养教育模式取代知识传授体系，这将是素质教育发展历程中的一个重要节点，意义深远.”

那什么是数学素养？数学素养属于认识论和方法论的综合性思维形式，它具有概念化、抽象化、模式化的认识特征.用南开大学顾沛教授的话说：“‘数学素养’就是把所学的数学知识都排出或忘掉后剩下的东西.”即在先天基础上，受后天环境、数学教育等影响，所获得的数学知识技能、数学思想方法、数学能力、数学观念和数学思维品质等融于身心的一种比较稳定的心理状态.

下面我以学生喜欢的足球问题为背景，分三个方面谈谈我对培养学生数学素养的肤浅认识.

1.用数学的视角去分析世界

问题：如图1，有一种足球由32块黑白相同的牛皮缝制而成，黑皮为正五边形，白皮为正六边形，一块白皮周围有3块黑皮，

图1每块黑皮周围有5块白皮，请问：缝制一个足球需要多少块白皮，多少块黑皮？（山西中考题）视角一：从五边形和六边形的边数着手.

一个正五边形有5条边，一个正六边形有6条边，从图中可以发现每个正六边形中恰好有3条边与五边形的边重合，而正五边形的每条边都与正六边形的边重合.因此，六边形的总边数为五边形的总边数的2倍.

解：设足球中有x块白皮，则有（32-x）块黑皮.

可列方程：6x=2×5（32-x）.

解得x=20.

当x=20时，32-x=12.

即：缝制一个足球需要20块白皮，12块黑皮.

视角二：从五边形和六边形的顶点个数出发.

从图形中可以发现，顶点的相交处总是两个六边形的顶点和一个五边形的顶点，因此，六边形的顶点总数为五边形的顶点总数的2倍，从而通过设未知数联立方程组解决这个问题.

视角三：从五边形与六边形的排列特点出发.

一个五边形周围有5个六边形，而一个六边形周围有3个五边形，若设有x个五边形，则有个六边形.因此，根据五边形和六边形的个数和等于32列方程，解决这个问题.

同一个问题，当用数学的视角去分析时，产生了不同的解法，给予了孩子更广阔的思考空间.

2.用数学的方式去思考问题

足球场上最精彩的就是射门，射门的角度决定了能否进球，可见踢足球是有“学问”的，以下用我们所学的几何知识分析足球射门的问题：如果两个点到球门的距离相差不大，要确定较好的射门位置，关键看这两个点分别对球门的张角大小，当张角较小时，则球容易被对方守门员拦截.

问题：在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到点A时，乙已跟随冲到B点（如图2）.此时甲自己直接射门好，还是迅速将球回传给乙，让乙射门好？（新疆中考题）

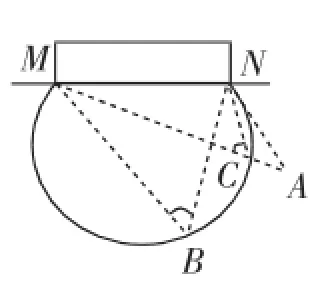
图2

分析：考虑过M、N、B三点作圆，显然，点A在该圆外，设MA交圆于点C，则根据“同弧所对的圆周角相等”可以得到：∠MBN=∠MCN.根据“三角形的一个外角大于与它不相邻的任一内角”，得∠MCN>∠MAN，所以∠MBN>∠MAN.

因此，甲应将球回传给乙，让乙射门.

通过热点问题考查学生综合运用数学的核心知识（平面直角坐标系、圆周角定理、三角形外角定理等）分析问题、解决问题的同时，还借助动态情境考查学生的分类思想、方程思想、模型思想及重要的数学方法——构造法，让学生在实际情景中用数学方式去思考问题.

3.用数学的方法解决问题

2014年在巴西进行世界杯比赛，其中巴西、墨西哥、喀麦隆、克罗地亚分在A组进行单循环足球比赛，争夺出线权，比赛规则规定：胜一场得3分，平一场得1分，负一场得0分.小组中名次在前的两个队出线.

提示：按积分多少排名次；积分相等的两队，净胜球数多的队名次在前；积分相同、净胜球数都相同的两队，进球数多的队名次在前.

如果克罗地亚队的积分为6分，问：克罗地亚能否小组出线？

学生如何去解决这个实际问题？把茫无头绪的实际问题转化为数学问题，通过数学的方法去解决.

方法1：如果小组中有一个队的战绩为全胜，克罗地亚队能否出线？

假设巴西队的战绩为全胜，根据下表可得：克罗地亚出线.

巴西墨西哥喀麦隆克罗地亚巴西—胜胜胜墨西哥负—负喀麦隆负—负克罗地亚负胜胜—

方法2：如果小组中积分最高的队积6分，克罗地亚队能否出线？

请按上面的方法进行分析，然后填空.

如积分最高的队积6分，则积6分的队可能有（1或2或3）个，当积6分的队（有1个或2个）时，克罗地亚队一定出线，当积6分的队（有3个）时，克罗地亚队不一定出线.

正如日本学者米山国藏曾经说过的：“数学知识可以记忆一时，但数学精神、思想和方法却永远发挥作用，可以受益终生，是数学能力之所在，是数学教育目的之所在.”

三、由“教为中心”转向“学为中心”

美国在培育学生的“21世纪素养”时，要求教师在教学过程中以学习者为中心，参照每个学生的知识和经验，满足他们独特的需要，使每个学生的能力都得到发展，并确保学生有真实的机会去运用和证明他们对“21世纪素养”的掌握.由“教为中心”转向“学为中心”，促进学生主动学习和合作学习的意识与能力，小组合作学习是很好的数学课堂实践模式.

遵循把学习的权利还给学生，把展示的机会还给学生，把交流的机会还给学生，把动手的机会还给学生，把选择的权利还给学生的原则，学生未学已懂的，老师不讲；学生自学易懂的，教师不讲；学生互助能懂的，教师不讲；讲了学生也基本不懂的，教师不讲；有学生能讲的让学生讲，教师也不讲！

小组合作学习主要有课前预习、互助对话、踊跃展示、大胆质疑、高效演练、总结提升六个步骤.

（1）课前预习：学生通过教师提供预习提纲，自主阅读课本，对书中提供的概念、定理、公式等边看边思考，弄清知识的来龙去脉.通过勾画圈点将预习中自己无法解决的问题、无法理解的知识等标记出来，通过预习发现自己的疑惑.

（2）互助对话：对预习中存在的疑惑，小组成员进行对话交流，让小组内的成员帮忙解决，再通过小组间的对话，生成共性的问题.

（3）踊跃展示：鼓励学生将小组间共性的问题拿出来展示交流，或者将小组在解决问题中得到的经验、方法等进行分享.

（4）大胆质疑：针对不同的学生在同一知识上不同的理解，让学生将自己不同的见解表达出来，从而使他们想得深、想得远，形成问为什么的好习惯，提高思维的深度.

（5）高效演练：教师精心设计练习题，让学生先独立思考，然后小组讨论，最后通过教师提问或学生板演的形式促进全班小组合作学习，创造性解决问题.

（6）总结提升：巧妙的课堂小结能达到“课虽终，趣犹存”的境界，通过学生谈学习体会、学习心得，谈学习中应注意的问题，教师再对所学内容进行归纳整理，深化所学知识，不仅能巩固知识、强化兴趣，还能进一步激起学生求知的欲望，使学生进一步产生对数学的兴趣、活跃学生的思维、开拓学生的思路，在愉快的氛围中把一节课的教学推向高潮.

课堂教学中学生成了主角，小组合作学习成了主要的学习方式，教学流程、教学理念、师生角色、教学模式的重构，让学生始终处于主体地位.走向素养导向的初中数学教学改革，定能培养出充满自信的人、能主动学习的人、积极奉献的人、心系祖国的公民.Z