对初中数学开放题编制的几点思考

☉福建省厦门市厦门一中海沧分校 王旭辉

对初中数学开放题编制的几点思考

☉福建省厦门市厦门一中海沧分校 王旭辉

初中数学新课程标准要求：“为了考查学生的创造能力，可以设计开放性问题.”这里的“开放性问题”就是本文所说的开放题.关于开放题的概念，没有唯一的答案，在我们初中数学中答案不固定或者条件不完备；具有多种不同的解法或有多种可能的解答；条件多余需选择，条件不足需补充或答案不固定及答案不唯一的问题等都可以称为开放题.开放题是种非常灵活的新题型，它的开放性主要在于它的问题的条件可以具有不完备性，答案可以具有不确定性，解题策略具有创新性等特点.

在实施素质教育的今天，培养初中生对数学的积极态度，使学生体验做数学的乐趣，提高初中生的数学素质，已成为中学数学教学十分重要的任务，同时，近些年在中考中考查开放性题目所占的比重也越来越大.因此，加强对初中数学开放题编制的研究就显得十分重要和有意义.

一、编制数学开放题的必要性分析

（一）有助于培养学生分析解决问题的能力

由于学生在解答开放题时，会表现出不同层次、多种水平的解答方案：有的学生可能只找到一种答案，有的学生能找到多种答案.不同的解答方案和结果会表现出不同的思维水平.学生通过探索的过程、寻找方法和计算的过程，变简单机械模仿过程逐步上升为深化提高知识的过程.在这样的解题过程中，学生分析问题、解决问题的能力得到培养和提高.

（二）有助于强化学生的创新意识

传统的封闭性题目答案是唯一的，学生往往找到一个答案就不必再进一步思考了.而开放题的答案一般需要根据不同的条件选择不同的结果.这样，可以培养学生不断进取的精神，强化学生的创新意识，提高学生养成创新习惯的自觉性.

（三）有助于形成宽松的教学氛围

由于开放题可达到教学形式的开放，使学生的学习可以是个别竞争，也可以合作完成；可以是畅所欲言，也可以是实践操作.在这一过程中，师生之间的教学关系已开放为平等的合作伙伴关系，学生可以怀着轻松、愉快的心情进行学习，有利于形成宽松和谐的课堂教学氛围.

（四）有助于培养学生的思维品质

开放题的教学，变单一的由教师讲解提问为师生共同研究问题的知识与能力的综合训练，变个体操作为集中交流合作，并触发思维的火花.这样，把开放性问题融入课堂教学中，可有效地激发学生敢于从多角度去思考问题，主动参与知识的建构过程，从而培养与发展学生思维的深刻性、广阔性、灵活性和创造性等良好品质.

（五）有助于学生体验数学的价值

由于开放题题材多数贴近学生生活实际，吸收并引进与现代工农业生产、科技等密切相关的具有时代性、地方性的数学信息资料，以丰富学生的数学认识.使学生把学习延伸到与之联系的现实生活中，并拓宽获得相关领域的新知识，从而认识到数学的价值，体验数学的本质.

二、数学开放题的编制类型

（一）从构成数学题系统的四要素出发来编制

从构成数学题系统的四要素出发，开放题的编制主要包括四类：条件开放题、策略开放题、结论开放题和综合开放题.

1.条件开放题

如果一个数学开放题，其未知的要素是假设，则称为条件开放题.这类开放题给出了结论，要求从多种不同角度去寻求这个结论成立的条件.

例1如图1，已知，在△ABC和△DCB中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加一个条件是________.

此题可以根据三角形全等的判定方法，从边、角等多方面去补充条件.

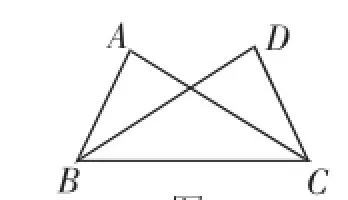
图1

图2

2.策略开放题

如果一个数学开放题，其未知的要素是推理，则称为策略开放题.这类开放题一般都给出了条件和结论，而怎样由条件去推断结论，或怎样根据条件去判断结论是否成立的策略未知，或者解法有多种.

例2小芸在为班级办黑板报时遇到了一个难题，在版面设计过程中需将一个半圆面三等分（图2），请你帮助她设计一个合理的等分方案.要求用尺规作出图形，保留作图痕迹，并简要写出作法.

此题可以通过三等分圆周角，或者把直径四等分等方法去解决.

3.结论开放题

如果一个数学开放题，其未知的要素是判断，则称为结论开放题.结论开放题就是给出了一定的条件，满足条件的答案有多个.

例3已知点P在第二象限，它的横坐标与纵坐标的和为1.则点P的坐标是______（写出符合条件的一个点即可）.

题目的结论很多，比如（-1，2）、（-3，4）等.

4.综合开放题

如果一个数学开放题，只给出一定的情境，其条件、解题策略和结论都要求解题者自行设定和寻找，这类问题称为综合开放题.

例4某家庭装饰厨房需用480块某品牌的同一种规格的瓷砖，装饰材料商场出售的这种瓷砖有大、小两种包装，大包装每包50片，价格为30元；小包装每包30片，价格为20元，若大、小包装均不拆开零售，那么怎样制定购买方案才能使所付费用最少？

此题的解决方法和瓷砖大小的选择都要由解题者来选择，答案虽然是唯一，但是过程却是开放的.

（二）从开放题答案的开口情况出发来编制

从开放题答案的开口情况出发，数学开放题可以分成三类：弱开放题、中开放题和强开放题.

1.弱开放题

弱开放题是指答案情况（包括可能情况）只有两种的开放题.

例5等腰三角形的两边长是4和6，则它的周长是_______.

这里要求我们分4为腰和6为腰两种情况去讨论.

2.中开放题

中开放题是指答案情况（包括可能情况）超过两种，但其数目是有限种的开放题.

例6桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图3所示，则这个几何体可以由______个这样的正方体组成.

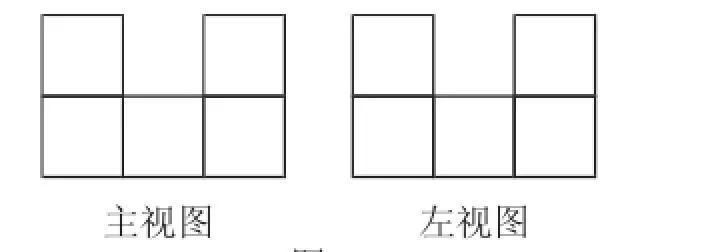
图3

满足条件的结论是有3种以上的，答案可以是8个、9个、10个或者以上，但是答案有限.

3.强开放题

强开放题是指只能给出部分答案情况，答案情况（包括可能情况）总数难以确定的开放题.

例7有一块边长为10米的正方形空地，现在要在空地上设计一个花坛，使花坛的面积是空地面积的二分之一，该如何设计？

此题的答案个数就难以确定了，因为花坛的形状千变万化，只要面积是空地面积的二分之一就可以了.

三、数学开放题的设计方法

好的数学开放题，能够充分体现出新的教育教学理念，加大教改力度，对教学的目标和学生的学习发展方向具有指导意义.现行教材中开放题数量较少，因此教师应该掌握开放题的设计方法.本文总结了如下四种方法：

（一）弱化成题的条件，使其结论多样化

把原题目的条件减少一个或两个，可以使题目的结论呈现开放性.

例8已知等腰三角形的底角比顶角大15°，求各内角的度数.

可以将条件改为：等腰三角形的两个内角之差为15°.这样就可以让学生考虑到等腰三角形的内角有底角和顶角之分，达到分类讨论思想训练的目的.

（二）在既定的条件或关系下，探讨多种结论

对于一些题目，在其条件不变的前提下，可以把题目的结论删去，让学生去发现，从不同的角度去考虑，得到的结果往往不同，从而达到开放的目的.

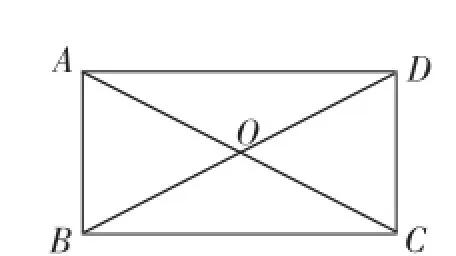
图4

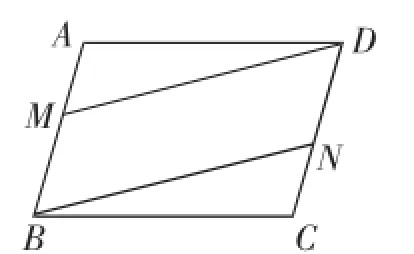
图5

例9如图4，矩形ABCD的两条对角线交于点O，且∠AOD=120°，你能说明AC=2AB吗？

可以将结论改为：你能从中得到什么结论？（至少写出三个）这样改变就可以让学生从边、角、对角线、三角形等多方面去考虑题目的结论了.

（三）给出结论，寻求使结论成立的充分条件

给出题目的结论，让学生寻找使结论成立的条件，同样可以达到题目开放的目的.

例10如图5，在平行四边形ABCD中，已知M和N分别是AB、DC边上的中点，试说明四边形BMDN也是平行四边形.

可以改为：如图5，在平行四边形ABCD中，要使四边形BMDN也是平行四边形，只需添加一个什么条件？

（四）加强结论，追加条件

对一个命题，对其结论进行加强，以研究得到这个结论需增加些什么条件，可得到一些开放题.

例11如图6，在平行四边形ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H，证明四边形EHFG是平行四边形.

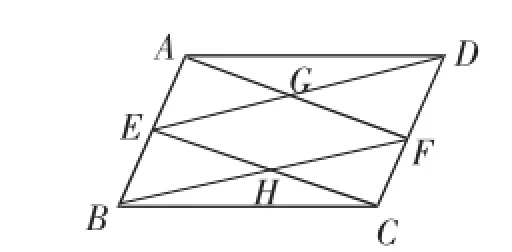
图6

可以把题目进一步补充：当添加什么条件时，可以使四边形EHFG变为菱形？

数学开放题是一种能很好地培养学生创新能力的新题型，它的编制还有很多奥妙的地方，有待在以后的题目编制中进一步的发掘.

1.中华人民共和国教育部.全日制义务教育数学课程标准（实验稿）［M］.北京：北京师范大学出版社，2001.

2.曾黄淑芳.初中数学开放性题目初探［J］.考试周刊，2015（45）.

3.钱丽娟.数学开放题研究及启示［J］.数学学习与研究，2015（11）.H