不同年级“关联”试题的命题实践与思考

☉江苏省南通市通州区兴仁中学 赵 建

不同年级“关联”试题的命题实践与思考

☉江苏省南通市通州区兴仁中学 赵 建

在各级考试中，对于重要位置的把关题、关键题来说，是随意复制粘贴各地所谓的考题到一次测试卷中还是精心挑战经典问题背景是值得每一个命题老师认真面对和深入思考的.在最近一次期中命题过程中，笔者参与了初二、初三的命题工作，在这次命题中，我们在两份试卷中分别设计了两道“关联”的数学把关题，考试之后得到两个年级师生的好评和热议，本文先给出这两道考题及命题意图，并跟进命题思考和教学导向，提供研讨.

一、两道“关联”的把关题

考题1（初二上学期期中考题）如图1，在Rt△ABC中，∠BCA=90°，AC＞BC，射线CM平分∠ACB.

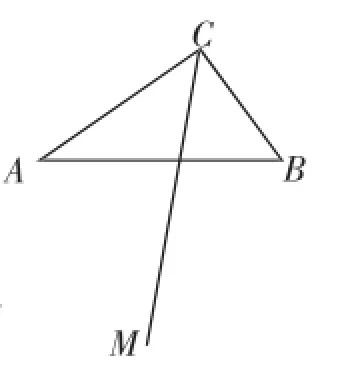
图1

（1）设CM交AB于点D，DE⊥BC于点E，DF⊥AC于点F，连接EF.求证：CD与EF互相垂直平分.

（2）若射线CM上有一点N到△ABC的顶点A，B的距离相等，连接NA，NB.

①请指出△NAB的形状，并说明理由；

②当AC=6，BC=4时，求四边形ANBC的面积.

命题意图：这道题源自人教版教材八年级上册习题.［1］只是强化了∠ACB是直角，重点考查角平分线的性质与判定定理、垂直平分线的判定与性质、全等三角形的判定与性质，对初二上学期的全等三角形、轴对称一章的知识重点考查、联合考查.解决第（2）题要注意第（1）问两条垂线段的启示作用，这样可以快速打开思路.

考题2（初三上学期期中考题）如图2，AB是⊙O的直径，AC是⊙O的弦，∠ACB的平分线CD分别交⊙O于D，交AB于M，连接AD、BD.

（1）请你过点D分别向AC、BC作垂线，垂足分别为点E、F，求证：四边形CEDF为正方形；

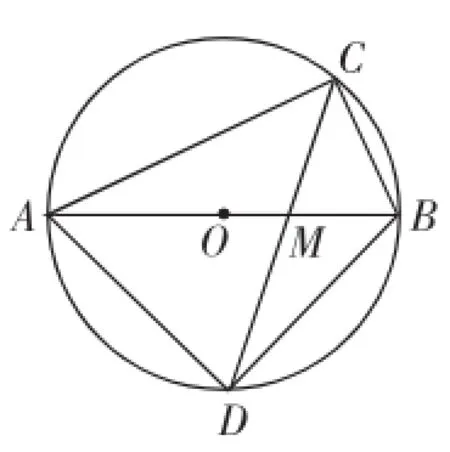
图2

（2）设DA=m，DC=n，试用含m、n的代数式表示△ABC的周长；

命题意图：这道题是在上面初二考题的基础上变换设问角度，融入了初三新学的圆、相似等知识点，使得探究方向进一步拓展.第（1）问证明四边形CEDF是正方形是常规问题；第（2）问进一步利用四边形CEDF是正方形，先证△ADE≌△BDF，得出AE=BF，从而代换得AC+ BC=2CE；再证△CDE为等腰直角三角形，所以CE=n，所以AC+BC=又AB是⊙O的直径，得∠ADB=90°.又CD平分∠ACB，所以AD=BD，所以AB=，即△ABC的周长=n.

第（3）问可以过点M向AC，BC引垂线段MG，MH，然后利用相似比和，相加得=1，而，即的值不变，这个不变值为

简要反思：第（1）问的正方形启示着第（2）问的AC+ BC=n.从而问题获得进展.第（3）问除上面利用比例式转化之外，还可借助于面积法处理.

二、“关联”试题的进一步思考

初中阶段很多试题的背景都是十分相像，但在不同年级不同章节中对其研究和解释的角度不一，就像需要灵活选用工具处理一样，本文提供的两道“关联”试题也是试图阐释这样的道理.以下就围绕“关联”试题的命题给出进一步的思考.

1.关联试题的命制要重视教材开发

认真研习初中版教材的同行应该知道，教材上的例题、习题不仅都是经典问题，而且相互呼应，若不加以对比研习，常常容易忽略不同分册教材之间的习题上的对应与关联.比如上文两道考题之间的关系，在初二、初三教材中都能找到原型.再如，初一图形初步知识学习之后，教材上曾安排学生度量三角形的内角和，再度量四边形的内角和，意图让学生通过度量这样的一种实验的方式直觉感知多边形内角和，为初一下学期学习和证明三角形内角和形成铺垫；该题还要求学生进一步取四边形的各边中点，并度量中点四边形的各边的长、各个内角的度数，发现中点四边形的对边相等、对角相等，这些实验操作其实都对应着初二年级要学习的平行四边形、中位线性质.如果我们不了解教材上的这些拓展习题的设计意图，不引导学生重视这些试题的开发与利用，则可能丢失了很多重要价值.

2.关联试题的问题背景要简洁好懂

关联试题的问题背景需要简洁好懂，这样可以减少学生“进入”该题的障碍，但是需要经过确认和识别才能进一步理解问题求解的方向与目标，并灵活调用相关数学知识实现求解.这里我们也可提及一些关联试题的问题情境，比如代数领域，以二次三项式为研究对象在初一可以引导学生辨别二次项式的次数、系数、项数；而在初二则可安排学生先运用整式乘法得到二次三项式，再逆向因式分解一个二次三项式，还可以基于完全平方式的角度对二次三项式的非负性、最值进行初步探究；到初三时，针对二次三项式可以从一元二次方程、二次函数的角度设计试题考查.这样来看，以二次三项式为背景的试题就是一个很有“数学味”的关联试题.

3.关联试题的求解力争能殊途同归

所选关联试题作为把关题的重要教学引领还在于，鼓励和引导师生在平时教学中重视那些解法可以殊途同归的试题，比如可以在不同年级选用不同方法的试题就值得充分关注.比如，几何领域，初二教材上曾要求学生解决过下面这道经典几何题：

教材习题如图3，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点.若∠AMN=90°，求证：AM=MN.

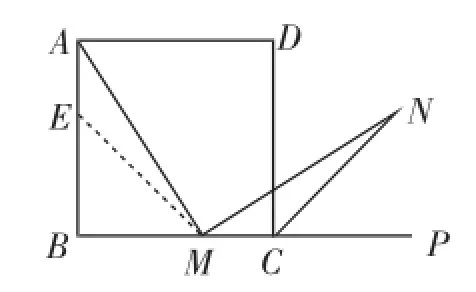
图3

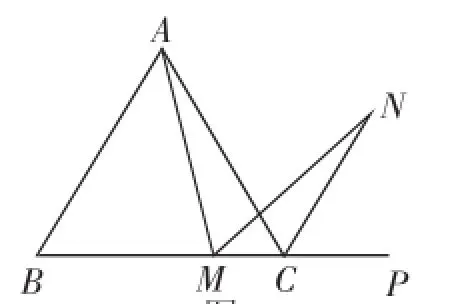
图4

初二的证明思路是这样的：在边AB上截取AE=MC，连接ME.在正方形ABCD中，∠B=∠BCD=90°，AB=BC.所以∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE.进一步证出△AEM≌△MCN，故AM= MN.

该题还可变式成等边三角形、正多边形的问题，比如下面的变式：

变式题1：正三角形ABC中（如图4），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由.

变式题2：正n边形ABCD…X，请你作出猜想：当∠AMN的度数是多少时，结论AM=MN仍然成立.

讲解：变式1，2的结论仍然成立.初二证明时还可继续采用截取的方式利用全等实现问题的解决.到了初三圆的学习之后，我们还可从结论出发，如图5，若连接AF，则Rt△AEF应该是等腰直角三角形，如果作出Rt△AEF的外接圆，有何发现呢？点C也在这个圆上吗？一个接近问题深层结构的“辅助圆”证法来到眼前！

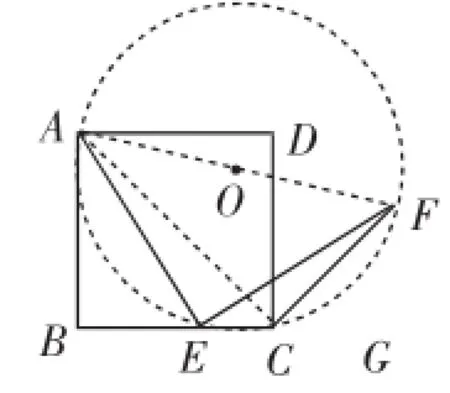
图5

图6

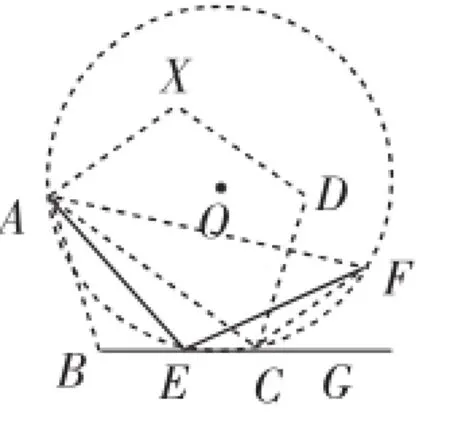
图7

重要的是，基于外接圆的思路，正三角形问题、正n边形问题也有类似的结构（如图6，图7）.

三、写在最后

有人说命题基本功是教师专业精进的突破口，笔者深有共鸣.一次考试常常影响着测试范围内的“全样本”的师生，不但作为一种教学反馈，更是一次教学诊断、评估和引领，我们提出在把关题处设置“关联”试题的想法还是初步的，也是个性化的一些认识，期待更多命题爱好者的题例跟进.

1.课程教材研究所中学数学课程教材研究开发中心，编著.义务教育教科书·数学·八年级上册［M］.北京：人民教育出版社，2013.

2.郑毓信.多元表征与概念教学［J］.小学数学教育，2011（10）.

3.陈爱军.预设互动促进对话，课件简约渐次展现——李庾南老师“函数的图像”课例赏析［J］.中学数学，2016（10）.

4.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

5.许燕.从解题赏析走向教学研究——以2016年无锡卷第27题为例［J］.中学数学（下），2016（10）.H