“问题”唤醒“沉睡”的数学复习课堂——对问题驱动下的数学复习课的感悟

☉浙江省宁波市鄞州区姜山镇中心初级中学 王 冲

“问题”唤醒“沉睡”的数学复习课堂
——对问题驱动下的数学复习课的感悟

☉浙江省宁波市鄞州区姜山镇中心初级中学 王 冲

《义务教育数学课程标准》中提出课堂教学应激发学生学习兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维.学生学习应当是一个生动活泼的、主动的和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式.因此，让学生主动、轻松、愉快地学习，已经成为当下课堂教学改革的主题.

在日常的教学过程中，笔者曾发现这样一个现象：在上新授课的时候，学生面对新知识的探索欲望强烈，能积极主动地参与到课堂活动中来；但是，上复习课的时候，学生面对旧知识的探索欲望显得有些低落，不能积极主动地参与到复习课堂活动中来，复习效率低下.同时，学生觉得数学复习课很枯燥、乏味.所以，笔者觉得有必要落实学生在数学复习课中的主体地位，激发学生在数学复习课上的学习兴趣，让学生在数学复习课中主动、轻松、愉快地学习.

著名数学教育家波利亚曾说过：“问题是数学的心脏.”而数学课堂正是在提出问题和解决问题的循环反复过程中培养、发展和提高学生的思维品质与学习能力的.同时，学生探究知识的欲望一般都是从问题开始的.所以问题应该是数学课堂的中心.因此，笔者认为，我们可以根据教学任务和学生学习的需要，将复习内容问题化，让学生自主、合作、探究学习，落实学生在复习课堂中的主体地位，激发学生的学习兴趣.同时，以“问题解决”获得知识与技能，提高学习能力和思维能力，促进情感、态度与价值观发展.

笔者结合自己曾经面向初二学生执教过的“直角三角形中求线段长度的方法”的教学片断，谈谈自己对问题驱动下的数学复习课的感悟.

一、问题驱动，生成相关方法

问题1：如图1，已知在Rt△ABC中，∠ACB=90°，AB= 10，CD是斜边AB上的中线，则CD=______.

生1：CD=5.

师：你是怎样求得的？你的依据是什么？

生1：直角三角形斜边上的中线等于斜边的一半.

（板书：①利用性质定理）

图1

图2

问题2：如图2，已知在Rt△ABC中，∠ACB=90°，AB= 10，∠B=30°，CD是斜边AB上的中线，你能求哪些线段的长度？

师：如果我再添一个条件，∠B=30°，你能求图2中哪些线段的长度？

生2：利用直角三角形斜边上的中线等于斜边的一半可以求得CD=5.

师：请你谈谈求解的过程并叙述其依据.

生3：因为∠ACB=90°，∠B=30°，所以根据30°所对的直角边等于斜边的一半，可以求得AC=AB=5.

（板书：②利用特殊角）

生3：因为∠ACB=90°，AC=5，AB=10，所以根据勾股定理可以求得.

（板书：③利用勾股定理）

生3：因为CD是斜边AB上的中线，所以根据三角形中线的意义可以求得AD=BD=AB.另外，根据直角三角形斜边上的中线等于斜边的一半，可以得到CD=5.

师：就是刚才生1总结的利用性质定理求直角三角形中的线段.

师：良好的开始是成功的一半，同学们已经总结了三种在直角三角形中求线段长度的方法，请大家思考一下，这三种方法在下题中是否适用？

问题3：如图3，已知在Rt△ABC中，∠ACB=90°，AB= 10，AC=6，CD是斜边AB上的高线，则BC=______，CD= ______.

生4：可以根据勾股定理求得BC的长等于8.

师：那么CD呢？

生4：可以利用面积法.

师：有点儿意思了，可以更具体些.

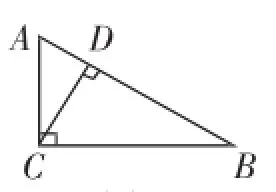
图3

生4：因为∠ACB=90°，AC=6，BC=8，所以S△ABC=AC· BC=24.又CD是Rt△ABC的斜边AB上的高线，所以S△ABC=AB·CD=5CD=24，因此CD=.

（板书：④利用面积法）

生5：我认为可以利用勾股定理求CD的长，因为CD是Rt△ACD与Rt△BCD的公共边，那么CD的计算方法有两种.第一种：CD2=AC2-AD2，第二种：CD2=BC2-BD2.如果设AD=x，则BD=10-x，所以可以得到方程36-x2=64-（10-x）2，解得x=，然后代入CD2=AC2-AD2，可以求得CD=

师：感谢你的发言，给同学们开启了另一扇思维的天窗.

师：当两个直角三角形有一条公共直角边的时候，我们可以利用勾股定理，构建方程模型求直角三角形中线段的长度.

感悟：回顾自己刚参加工作的时候，上复习课习惯于先梳理、归纳知识点，然后讲解一两道典型例题，接着让学生进行课堂练习，检测学生的掌握情况.现在想想，这种形式的复习课，学生被动地接受复习内容，没有经历思考、探索等体验活动，导致学生不能积极主动地参与到课堂活动中来，复习效率低下.同时，学生也觉得数学复习课很枯燥、乏味.所以，在本次“直角三角形中求线段长度的方法”的专题复习课中，笔者摒弃了传统复习课的基本思路.

课堂伊始，笔者就抛出了一道已知直角三角形斜边长，求斜边上中线长的题目.笔者再提出“递进式问题”———你是怎样求得的？你的依据是什么？引导学生主动归纳出直角三角形中求线段长度的方法之一：利用性质定理.问题2是问题1的延伸，在问题1的基础上添加了一个特殊角的条件.此时，笔者提出一个“开放性的问题”———你能求哪些线段的长度？不再局限于学生求某条线段的长度，旨在让学生从多角度去探究直角三角形中求线段长度的方法.问题3是问题2的拓展，在解决问题2的过程中，学生已经主动探究出了直角三角形中求线段长度的的另外两种方法：利用特殊角；利用勾股定理.所以，学生很轻松地求得了BC的长.这时，笔者就提出了一个“引导性问题”———那么CD呢？引导学生积极主动地去探究求CD的方法.这样就出现了直角三角形中求线段长度的第四种方法：利用面积法.同时，生5利用勾股定理，构建方程模型求直角三角形中线段的长度的方法，让学生在亲身经历解决问题的过程中，不仅领略了数形结合思想和方程思想的魅力，而且很好地处理了知识与方法应用之间的关系，提高了复习课的效率.

通过三个“循序渐进式的问题”，让学生去求解直角三角形中的线段长度，并叙述求解过程及依据，使学生轻松、自主地复习了与求直角三角形中线段长度有关的知识与方法，通过让学生自主、探究学习，激发学生的学习兴趣.同时，学生通过亲身经历求直角三角形中线段长度的过程，主动构建了直角三角形中求线段长度的方法的知识网络.

二、更换背景，促进知识迁移

师：我们从边、角入手梳理了直角三角中求线段长度的方法，同时对解决直角三角中求线段长度的方法也有了进一步的体验.下面让我们继续探究.

问题4：如图4，已知在Rt△ABC中，∠ACB=90°，AC=6，AB=10，且AD是△ABC的内角∠CAB的平分线，求BD的长.

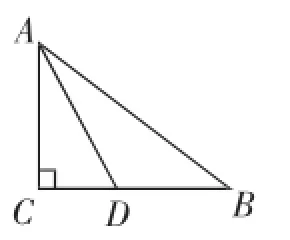
图4

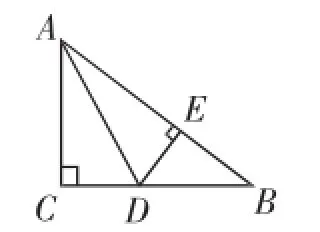
图5

师：大家好像遇到了困难，刚才我们归纳了在直角三角形中求线段长度的四种方法，而现在BD不在直角三角形中，我们该怎么办？

生齐答：可以构造直角三角形.

师：如何构造？

生齐答：过D作DE⊥AB于E.

师：当所求的线段不在直角三角形中时，我们可以通过作垂线将一般三角形转化成直角三角形，我们把这种数学思想称为转化思想.

师：同学们，观察图形，你们发现了哪些结论？

生6：因为AD是△ABC的内角∠CAB的平分线，∠ACB=90°，DE⊥AB，所以根据角平分线的性质可以得到CD=DE.

生7：根据刚才生6的结论CD=DE，再结合∠ACB= 90°，DE⊥AB，AD=AD，就可以证明△ACD≌△AED，所以AE=AC=6.

师：非常棒，现在以小组为单位讨论解决这道题的不同方法.

师：A组把你们集体讨论的成果跟大家分享一下.

A组：第一种方法：先根据勾股定理求得BC=8.设BD= x，则CD=8-x.结合刚才生6和生7发现的结论，可以得到DE=CD=8-x，BE=AB-AE=AB-AC=4.所以在Rt△BDE中，根据勾股定理，列出方程x2=（8-x）2+42，解得x=5，即BD=5.

第二种方法：因为∠ACB=90°，所以S△ABC=AC· BC=24.由DE⊥AB，得S△ABC=S△ACD+S△ABD.设BD=x，则DE= CD=8-x.可以得到关于x的一元一次方程×6（8-x）+× 10（8-x）=24，解得x=5，即BD=5.

第三种方法：因为∠ACB=90°，所以S△ABD=AC· BD.由DE⊥AB，得S△ABD=AB·DE.设BD=x，则DE=CD= 8-x.可以得到关于x的一元一次方程×6x=×10（8-x），解得x=5，即BD=5.

师：集体的力量真是大，想出了那么多方法.我也跟大家分享一下我的想法.刚才大家发现△ACD≌△AED，也就是说如果将△ACD沿AD所在的直线对折，△ACD与△AED将互相重合.所以，我们可以把它归类于折叠问题.当在直角三角形中碰到折叠问题时，我们就可以利用面积法或利用勾股定理构建方程模型求线段的长度，请看直角三角形中的折叠问题.

问题5：如图6，已知在Rt△ABC中，∠ACB=90°，AC=6，AB=10，沿DE所在的直线折叠，使得点A与点B重合，折痕DE交BC于D，交AB于E，求BD的长.

师：分析条件，大家能得到哪些结论？

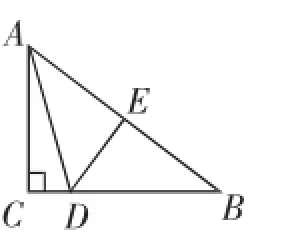
图6

师：你的思维真敏捷，一下子发现了这么多结论，结合生8发现的结论，哪位同学可以帮忙解答？

生9：根据生8发现的结论，设BD=x，则AD=BD=x， CD=8-x.因为∠ACB=90°，所以62+（8-x）2=x2，解得，即BD=.

师：你表达得特别清楚，让大家一听就懂.当某条线段所在的直角三角形无法求解时，我们不妨通过数量关系转化到另一个直角三角形中，求与之相关的线段的长度.

感悟：问题4的设置建立在前三个问题的基础之上，此时学生已经基本掌握了直角三角形中求线段长度的四种方法.所以，笔者提出思考力度较大的问题，有部分学生一时之间难以想到解题思路.这时，笔者就提出了一个“引导性问题”———大家好像遇到了困难，刚才我们归纳了在直角三角形中求线段长度的四种方法，而现在BD不在直角三角形中，我们该怎么办？让学生自主去探究发现可以过D作DE⊥AB于E，构建直角三角形.然后，笔者又提出了一个“引导性问题”———观察图形，你们发现了哪些结论？通过这两个问题，学生拾级而上，主动探究发现CD=DE，△ACD≌△AED，为问题的解决奠定基础.

“义务教育数学课程标准”在7～9年级的学段目标中提出：让学生经历从不同角度寻求分析问题和解决问题的方法的过程，体验解决问题方法的多样性，掌握分析问题和解决问题的一些基本方法；在与他人合作和交流的过程中，能较好地理解他人的思考方法和结论.所以，笔者让学生通过小组合作的形式探讨问题4的多种解法，培养学生从多角度思考问题的习惯，同时也让部分学生主动发现自己在求直角三角形中线段长度时方法方面的缺漏，亲身经历解决问题的过程，掌握解决问题的方法，主动弥补缺漏的知识，形成对知识的深层次理解.最后，笔者引导学生发现问题4可以类比于折叠问题，为探究问题5埋下伏笔，培养和提升学生举一反三、触类旁通的能力.

以“问题”代替直接复习知识点，充分激发学生在数学复习课堂中的探究欲望，落实学生在数学复习课堂中的主体地位.学生通过亲身经历求直角三角形中线段长度的过程，主动构建直角三角形中求线段长度的方法的知识网络.同时，“问题”助推了师生互动与生生互动，学生不再是“静止”状态，而是积极主动地参与到教学活动中来.所以，笔者认为，教师在上复习课的时候，应该以“问题”代替直接复习知识点，引发学生积极主动地参与到教学活动中来，通过问题让学生自主归纳，总结知识点和方法，使学生在数学复习课中主动、轻松、愉快地学习.

1.王建波.初中数学新课程标准［M］.北京：北京师范大学出版社，2012.

2.黄勤新.问题，数学的心脏——数学课堂观察反思［Z］.百度文库.

3.陈锋，薛莺.以问题引领，提升复习效能——对初三“圆的复习”课几个片段的感悟［J］.中学数学（下），2013（5）.

4.朱绍志.“问题引领，自主学习”的教学探讨——《一元一次不等式》复习课实录与反思［J］.中小学数学（中学版），2012（6）.

5.姜晓翔.“问题串”引领下的“导学式生本课堂”——由一堂“平行四边形性质与判定”的复习课说起［J］.上海中学数学，2012（12）.

6.覃小平.以问题为中心引领教学，以思维为核心促进发展——小学数学“以问导学”教学方法探究［J］.广西教育（小教版），2012（1）.Z