铺平垫稳拾级而上，引导回顾反思提升——中考综合题教学的一些思考

☉江苏省江阴市石庄中学 姚卫金

铺平垫稳拾级而上，引导回顾反思提升
——中考综合题教学的一些思考

☉江苏省江阴市石庄中学 姚卫金

在当前的中考复习背景下，初三第二学期在中考备考期间，学生会接触大量综合题，这里所指的综合题是指综合了多个知识点且难度较大的试题，题型有选择、填空、解答，以解答为主.这类试题在讲评时如果简单的告知答案或思路，往往难以取得较好的教学效果，我们在中考综合题教学中积累了一些教学经验，比如，增设铺垫，引导学生拾级而上，解后安排学生回顾反思，积累问题的深层结构或本质特点.本文以近期收集的一些典型综合题，呈现讲评记录，并跟进思考，提供研讨.

一、综合题解题教学案例

考题1（上海宝山区初三一模考题）已知：如图1，两块全等的斜边为10cm，含30°角的直角△ABC和直角△ACD按如图放置，在将△ACD以1cm/s的速度沿AC的方向匀速平移至△PNM位置的同时，点Q从点C出发，沿着CB方向也以1cm/s的速度匀速移动，如图2，当P与C重合时，点Q停止移动，设AP=x，连接PQ、MQ、MC.

（1）当x为何值时，PQ∥MN？

（2）设△QMC和四边形ABQP的面积比为y，求y与x之间的函数关系式.

（3）求使△PQM为直角三角形时AP的值.（若不可能，请说明理由）

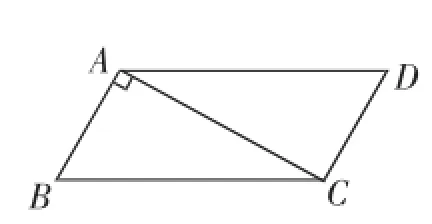
图1

图2

解题教学记录：我们主要预设了如下一些问题，帮助学生设计了铺垫，使得学生在这些铺垫问题的基础下，自主发现问题解答.

比如第（1）问的讲评时设计如下一些问题：

问题1：在平移过程中，分析MN与AB的位置关系，并说明理由.（预设：因为∠BAC=∠MNP=90°，所以AB∥MN）

问题2：当PQ∥MN时，PQ与边AB有怎样的位置关系？

问题3：当PQ∥MN时，PQ与边AC有怎样的位置关系？

问题4：用含x的式子表示PC的长.

设计意图：在上述铺垫问题启发之生，学生可将目光聚焦在直角△PCQ中利用锐角三角函数来列出方程获得解答.

第（2）问的讲评时预设如下的一些问题：

问题5：在平移过程中，PM与BC边有怎样的位置关系？

问题6：有人认为，在平移过程中，恒有△PQC与△MQC的面积相等.你觉得道理何在？

问题7：如图3，作PG⊥BC于G点，试用含x的式子表示PG.

问题8：用含x的式子表示△PQC和△MQC的面积.

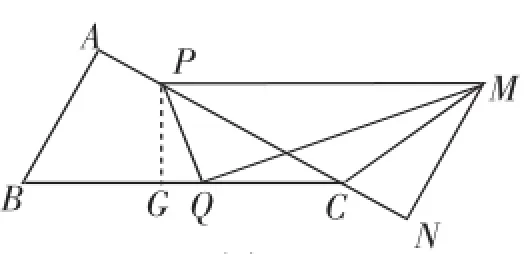
图3

问题9：用含x的式子表示四边形ABQP的面积.

设计意图：在上述铺垫问题启发之生，学生可将△QMC和四边形ABQP的面积比为y用含x的式子表示出来.

第（3）问的讲评时预设如下的一些问题：

问题10：在运动过程中，∠MPQ为直角时，求x的值.

问题12：求使△PQM为直角三角形时AP的值.

设计意图：通过前两问的分别求解，暗示了原考题第（3）问的解答.

解后反思：

问题13：解决本题时你发现哪一类特殊直角三角形是很关键的？为什么？

问题14：解决本题过程中，你还能积累哪些基本图形或性质？

问题15：第（3）问为什么只要考虑两处直角的可能？你是根据什么直接舍去一种情形的？

考题2（江苏海门中学自主招生考题）已知：在平面直角坐标系xOy中，双曲线与直线y=-x+k都经过点M，且OM=2，求k的值.

解题思路：这道题看上去非常简洁，然而需要解读的信息量很大，且十分隐蔽，需要调取不同知识领域的数学工具综合求解.比如条件“OM=2”本质上是以原点为圆心，2为半径的圆一个动点M；而双曲线与直线的一个交点又恰为M点，也即点M应该是三个图形的交点.于是可以联立双曲线与直线方程得到关于k的一元二次方程，再把点M的条件利用起来（设点M的坐标为（m，n），则m2+n2=4），组合方程组实现求解.

一是防汛抗旱取得积极成效。2013年，河南省因持续高温少雨，发生了较为严重的春旱、伏旱和秋旱。全省累计投入抗旱资金22.2亿元，累计抗旱浇地13 349万亩次，解决21.94万人临时性饮水困难，挽回经济作物损失22.53亿元、粮食作物损失88.58亿元。完成了56个平原县计算机网络、视频会商系统和264个山丘乡（镇）视频会商系统建设，完善了防汛抗旱指挥体系。

教学预设：

问题2：在坐标系中，OM=2，则点M在哪种图形上？

问题3：设点M的坐标为（m，n），则m，n之间有怎样的数量关系？（m2+n2=4）

问题5：设点M（m，n）为“问题4”中关于k的一元二次方程的两根，则可得关于m，n的哪两个等式？能否联立并解出m，n？解出的m，n是否都符合题意？

最后，在学生充分讨论的基础上，给出本题完整解答如下：联立得，化简并整理得，因为OM=2，所以OM2=4，所以x2+（-x+，设点k）2=4，整理得2（x2-kx）+3k2-4=0，由（*）得x2-kx=-2k，则2（-2k）+3k2-4=0，解得k1=2，k2= -.经验证：当k=-时，Δ＞0，当k=2时，Δ＜0，所以k的值为-.

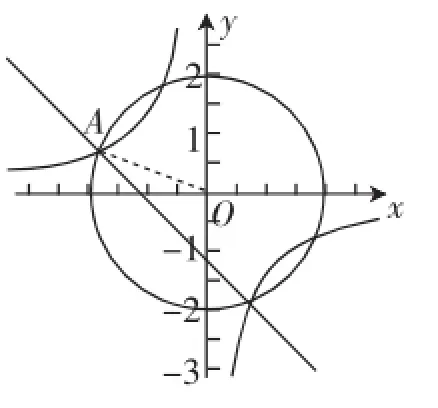
图4

反思时给出本题的图像结构，如图4所示.

二、关于综合题讲评的进一步思考

1.深刻理解综合题思路，充分展开解法步骤，想清思路的自然生成

理解教学内容，即弄清教什么永远是教学的经典问题.只有在弄清教什么之后，才能进一步思考怎么教的话题.当我们还没有弄清一道试题解题思路怎样贯通，有哪些不同的贯通路径，不同的思路对应着哪些数学概念或解题念头，对比不同的思路，发现哪些思路更能体现“回到概念去解题”的自然、简洁的特点.这些是作为教师解题的一些思考方向，而不只是满足于贯通思路，获取答案的“低级阶段”.

2.预设铺垫式问题，引导学生调动已有数学概念或解题经验

在教师对综合题达到了深刻理解之后，就需要思考“怎样教”，即怎样把“冷冰”的解题思路以启发学生“火热思考”中自主发现难题的突破思路，让学生不但学会解题，更重要的获得自主发现思路的愉悦感.而这些铺垫式问题需要从简单的阅读理解条件信息出发，以简单的思考开始，渐次生长，并引导学生合并来自不同条件信息的进展，获得思路贯通.当问题在强化条件不断添加后，还要引导学生兼顾前后不同的问题，使得思路的连通变得自然而合理.

3.重视解后回顾与反思，提示问题深层结构或直观形式

较难题讲评之后如果缺少必要的回顾反思环节，往往是“入宝山而空返”（罗增儒语）.在学生下次再遇类似问题常常又是懂而不会，或者会而不对.所以在这类难题讲解之后需要跟进必要的回顾与反思，使得学生对该题的深层结构、本质特点有更深的认识，如果能与学生已有解题经验“联通”，并入到此前积累的一些解题模型或经验中，则可以达到对一类问题的深刻理解，从而追求“做一题，会一类，通一片”的解题效果.

4.跟进变式再练，反馈综合题讲评效果

近两年，《中学数学》（初中版）发表了很多解题教学的文章，其中不少文章都倡导开展听课检测的教学环节，笔者也深受教益，并在教学工作中积极开展变式再练活动，取得较好的效果.作为文末，我们也对上文中“考题1”给出一道变式再练题，提供研讨.

变式再练：（上海宝山区初三一模考题，改编）题干不变，这里略，见上文.

（1）求证：PM∥BC.

（2）用含x的式子表示△PQC的面积.

（3）当x为何值时，四边形ABQP的面积取得最大值？

（4）当x为何值时，△PQC与△PMN相似？

（5）△PQM可能为直角三角形吗？如果可能求出x的值，如果不能，说明理由.

1.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

2.郑毓信.善于提问［J］.人民教育，2008（19）.

3.孟慧.几何综合题研究：从思路贯通到教学微设计［J］.中学数学（下），2016（9）.

4.杨卫东.客从何处来：一道几何把关题的命制历程［J］.中学数学（下），2016（8）.

5.孙莉.思路生成贵在自然，一题一课追求简约——一道考题的思路突破与习题课设计［J］.中学数学（下），2016（9）.

6.吴忠妙.一道考题的思路、难点与教学设计［J］.中学数学（下），2016（9）.H