基于评价指标的EIT算法参数选择方法研究

陈晓艳，常晓敏

(天津科技大学电子信息与自动化学院，天津 300222)

基于评价指标的EIT算法参数选择方法研究

陈晓艳，常晓敏

(天津科技大学电子信息与自动化学院，天津 300222)

为客观准确地选择EIT算法参数，采用8种评价参数指标对共轭梯度算法的迭代次数和Tikhonov正则化算法的正则化因子的选择进行研究．首先，构建EIT正问题模型，并求得两种算法的逆问题解；然后，根据8种评价参数的定义，获得图像重建时的最佳参考值范围：共轭梯度迭代算法的迭代次数在70～80次，正则化因子的取值范围为0.01～0.1．为了验证上述结论，重建EIT图像，并进行对比分析．结果表明：基于评价指标获得参数重建图像的效果更令人满意；针对参数选择，提出的方法可为其他电阻抗图像重建算法提供一种客观的评价依据，为EIT图像质量评价体系的构建奠定基础．

EIT算法；参数选择；共轭梯度迭代法；Tikhonov正则化算法；评价标准

电阻抗断层成像技术(electrical impedance tomography，EIT)是近几年发展起来的新兴医学成像技术，由于其具有无辐射、廉价、响应快等特点，在医疗诊断和生物研究等领域有广阔的应用前景．电阻抗断层成像技术根据物场中介质的电特性，通过施加激励电流来获得相应的电压，以此来估计物场内介质电导率分布或电导率变化，因为不使用超声、射线、电磁波等技术，所以对人体无损害，并且可以多次不间断重复测量，成本低廉，是一种理想的无损伤医学成像技术[1-3]．

目前，EIT重建算法已被广泛关注，不断有新的算法被提出[4-6]．国内外的研究主要是集中在算法的改善、提高空间分辨率和减小计算量等方面，而对于各种算法的参数选择尚缺乏客观的、科学的、统一的衡量指标．

本文以共轭梯度迭代算法[7-8]和Tikhonov正则化算法[5，9]为例，采用8种指标分别对迭代次数和正则化因子进行选择，旨在探索一种能客观科学地选择算法参数的方法．8种指标分别是图像相对误差、图像相关系数、结构相似度、振幅响应、位置误差、分辨率、外形形变和瞬时震荡，前3项指标常用于图像质量评价[5，10]；后5项指标是由Adle等[11-12]于2009年提出的，并在EIDORS软件中所采用．

1 评价参数指标

1.1 图像相对误差

图像相对误差的计算公式为

式中：σ∗表示原始图像真实电特性分布；σ表示重建图像的电特性分布．

图像相对误差ER用来衡量真实图像与重构图像之间的偏差；图像相对误差越小，反问题求解(图像重建)的质量越好，重建图像的质量也就越高．

1.2 图像相关系数

图像相关系数的计算公式为

式中：Ne为重建图像的单元数；σ∗表示原始图像真实电特性分布；σ表示重建图像的电特性分布；、分别为重建值和原始值的平均值．

图像相关系数r用于判断重建图像与真实图像之间的相关程度，这一性能指标可以有效地权衡重构图像的好坏，取值范围为0～1．图像相关系数r越大，相关性越强，重建图像的质量越高．

1.3 结构相似度

结构相似度的计算公式为

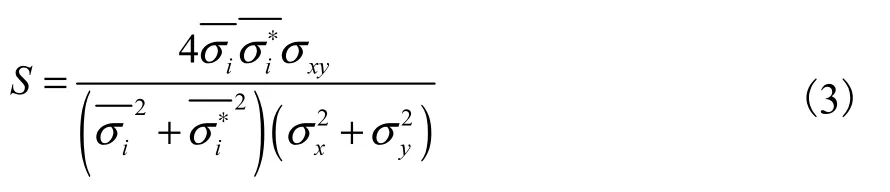
结构相似度S表示重建图像对于所建模型的非线性改变程度，取值范围为[0，1]，当S越接近1时，表明重建图像与真实图形之间的像素有越高的相似度，对所建模型有越小的非线性改变，重建图像的质量越高．

1.4 振幅响应

振幅响应的计算公式为

式中：Δσ=σt−σr，σt是加入目标之后的电导率(即满场电导率)，σr是均匀场域的电导率(即空场电导率)；[]k是重建图像中每个单元的电导率；Vt是球形目标的体积．

振幅响应RA代表了重建图像的像素振幅与电导率归一化差值的比值．对于目标的任意位置，RA的值都应是恒定不变的．否则，如果目标在场域中处于不同位置时，就会呈现不同的RA，从而呈现不同的电导率值，这对于图像判读有严重影响．

1.5 位置误差

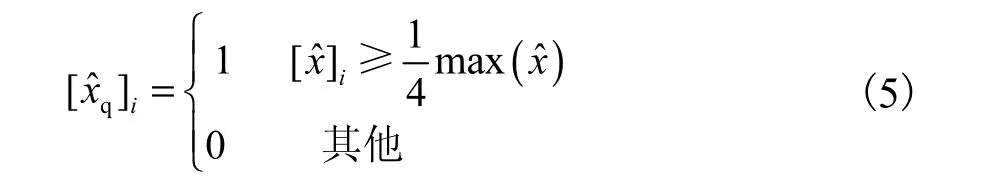
位置误差的计算公式为

式中：rt是的重心到场域中心的距离；rq是的重心到场域中心的距离．

位置误差EP体现了重建图像真实地表现目标真实位置的程度，EP应该尽可能小，且目标位于不同位置时，EP应能显示出变化．

1.6 分辨率

分辨率的计算公式为

为了能够准确反映目标电导率分布的轮廓，分辨率R的值应该是一致的，并且值要小．非一致的R会引起对大目标进行重建时的重建位置的错误，R越小，相邻目标的区分度越高．

1.7 外形形变

广播影视主要是根据观众的需求以主动的方式给他们提供，自行选择收看节目的公共服务。在数字条件下，我们不但要提供公共服务，还要提供多样化、个性化的服务。因此，节目内容生产将面临前所未有的巨大需求和挑战，这就要求传播内容要适应社会发展，从封闭、分散、独立的传统服务模式向开放服务、个性化服务、信息聚合服务转变，按照社会化规律和市场的要求，进行结构调整、资源重组、合理分工、高效运行。

外形形变的计算公式为

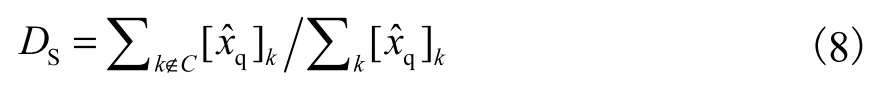
外形形变DS体现了重建目标的形状偏差程度，DS的值应一致，且足够小．较大的DS会造成对图像的分析不正确．

设C为以重建目标xˆq的重心为圆心的圆，面积与Aq相等．本文所建模型中，成像目标为圆形，故重建目标也应是圆形的，若重建目标xˆq的某些元素不在圆形范围内，则表示重建图像中的目标产生了形变，超出了轮廓的边界，与原始的目标无法吻合．

1.8 瞬时震荡

瞬时震荡的计算公式为

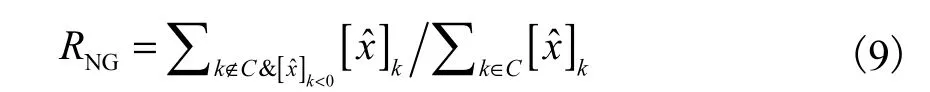
瞬间震荡RNG用于评价重建图像对于目标区域的异号程度(是否有伪影及伪影程度)，RNG应是一致的，且足够小．

2 参数的选择

在COMSOL Multiphysic的平台上，建立正问题模型．模型是半径为9,cm的16电极圆形场域，场域中心坐标为[0，0]，目标圆的中心坐标为[－4，2]，半径为2,cm，设定场域的传导率为0.01,S/m2，目标圆的传导率为1,S/m2，选用钛电极，电极宽度的占空比为20%,，并选取相邻激励测量的工作模式．采用共轭梯度算法进行逆问题的求解，迭代次数N取1～100．按照式(1)—式(9)计算各指标，获得各项指标(纵坐标)随迭代次数(横坐标)增加而变化的曲线，见图1．

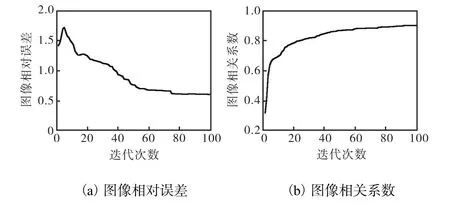
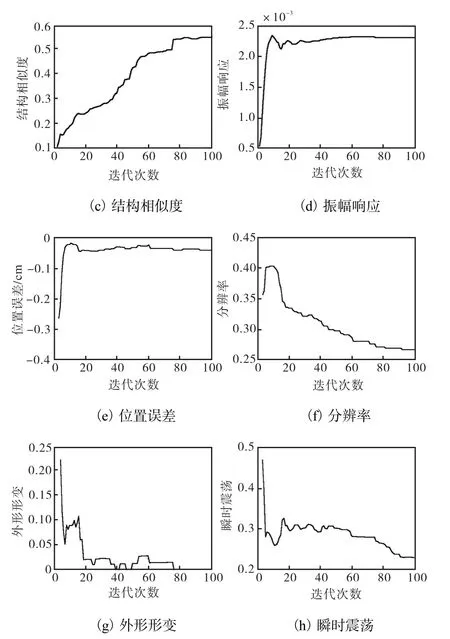
图1 不同迭代次数时的性能指标曲线Fig. 1 Performance index curves of different iteration times

为了更清晰地在图1中显示各参数指标的变化情况，图中纵坐标尺度是不同的．根据数据可以得到如下推论：

图像相对误差ER随迭代次数增加呈现指数衰减趋势，当N＞50，衰减缓慢；当N＞85，衰减至最小(N＝100，ER值为0.607)．

图像相关系数r随迭代次数增加呈现指数增加趋势，当N＞20，增速减慢；当100＞N＞70，r值相近，且最接近1(N＝100，r值为0.899)．

结构相似度S随迭代次数增加呈现抛物线增加趋势，当N＞60，增加缓慢；当100＞N＞75，S值几乎不变，且达到最大(N＝100，S值为0.551)．

振幅响应RA随迭代次数增加总体保持不变．位置误差EP随迭代次数增加在[-0.263,4，-0.018,5]内小幅变化．

分辨率R随迭代次数增加呈现指数衰减趋势，当N＞60，衰减缓慢；当N＞75，衰减至最小．

外形形变DS随迭代次数增加呈现减小的趋势，当N＞75，减小至最小(N＝100，DS趋于零)．

瞬间振荡RNG随迭代次数增加呈现抛物线衰减趋势，当N＞90，衰减至最小(N＝100，RNG值为0.231)．

总之，根据各指标的含义和其曲线图的总体大小、整体走向以及收敛性，可推断当迭代次数取[70，80]区间时，重建图像综合指标均呈现满意效果．

为了验证上述结论，针对给定的具体模型，在Matlab仿真环境中得到图2所示的重建图像．

从图2可以看出：3种迭代次数的成像结果与性能指标的参数选取是吻合的，迭代次数为70时，伪影较小，空间分辨率较高，重建质量较高；尽管当N＝100时，重建图像的质量要略优于N＝70，但消耗的求解时间会增大，选取N＝70可以达到相对满意的效果．

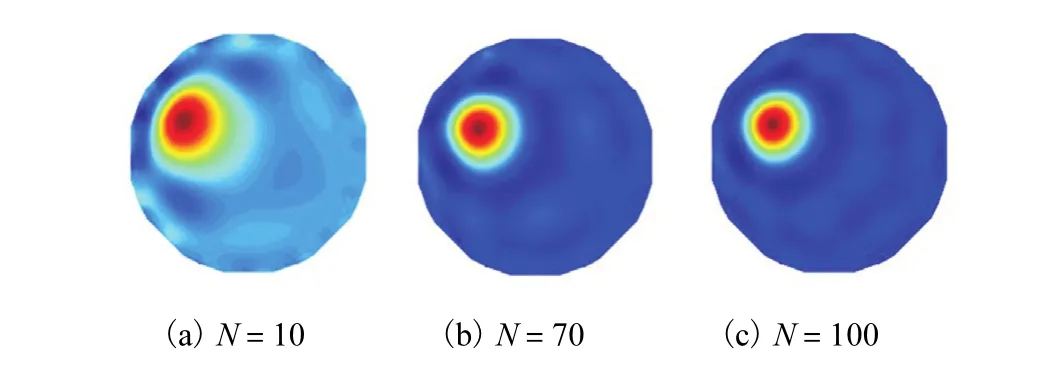
图2 不同迭代次数时的重建图像Fig. 2 Reconstructed images with different iteration times

2.2 Tikhonov正则化算法中正则化因子α的选取

根据正则化算法的原理，不同的正则化参数α的选取，会直接影响阻尼作用的强弱，最终会导致逆问题的解不同．在[0，1]区间，按照8项指标计算式(1)—式(9)，获得各项指标(纵坐标)随正则化因子(横坐标)增加而变化的曲线，见图3．

图3 不同正则化因子时的性能指标曲线Fig. 3Performance index curves of different regularization factors

从图3可以看出：根据各指标的含义和其曲线图的总体大小、整体走向以及其收敛性，当正则化参数α取较小值(0.01～0.1)时， ER、r、S、RNG指标表明，图像质量较好；RA值在[2.242×10-3，2.276×10-3]，区间也十分稳定，EP集中分布在[－0.046，0.012]区间，R在[0.225，0.236]区间变化，DS在0～0.06内变化，说明了这4项指标受正则化因子影响较小．

根据文献[5]提出的正则化图像重建算法，针对上述模型，分别取3个不同参数α进行图像重建，结果如图4所示．从图4可以看出，当正则化因子α逐渐增加时，目标形状愈加不规则，轮廓愈加模糊，伪影逐渐增大，分辨率逐渐下降，成像效果逐渐变差，这说明图像重建的质量逐渐变低．

图4 不同正则化因子时的重建图像Fig. 4Reconstructed images of different regularization factors

3 结 语

本文在分析8种评价参数指标的定义和共轭梯度迭代法、Tikhonov正则化算法两种EIT算法原理的基础上，利用有限元仿真软件COMSOL和Matlab建立场域目标，得到两种算法的性能指标曲线图；根据曲线图选取了两种EIT算法较适合的参数，迭代次数N在[70，80]区间，正则化因子α在[0.01，0.1]区间；最后根据图像重建算法，将选择的参数与其他参数的重建效果进行对比，验证了采用本文根据评价指标所选择的参数进行图像重建的效果．

在采用评价指标进行EIT算法参数的选择时，需要根据正问题模型求得雅克比矩阵J，计算TJ J，然后根据文献[5]的Tikhonov算法进行逆问题求解．当正问题模型发生改变时，由于矩阵J的改变，而导致8项评价指标发生改变，需要重建计算指标，获得新的算法参数的参考值，即可获得满意的成像效果，可避免因算法参数选择的不恰当导致成像效果不理想．

本文提出的方法可为其他电阻抗图像重建算法的参数选择提供一种客观的评价依据，从而为构建EIT图像质量评价体系奠定基础．

［1］ Bayford R H. Bioimpedance tomography(electrical impedance tomography)[J]. Annual Review of Biomedical Engineering，2006(8)：63-91.

［2］ 陈晓艳，张静. 采用阈值修正法改善电阻抗图像质量[J]. 中国生物医学工程学报，2011，30(4)：481-486.

［3］ Chen X Y，Wang H X，Zhao B，et al. Lung ventilation functional monitoring based on electrical impedance tomography[J]. Transactions of Tianjin University，2009，15(1)：7-12.

［4］ 陈民铀，杨艳丽，何为，等. 基于粒子群优化算法的电阻抗图像重建[J]. 重庆大学学报，2011，34(1)：82-87.

［5］ 陈晓艳，房晓东. 一种新的正则化图像重建算法及参数优化[J]. 天津科技大学学报，2014，29(6)：74-77.

［6］ 杨琳，徐灿华，付峰，等. 一种基于加权频差阻尼最小二乘的准静态EIT算法[J]. 仪器仪表学报，2013，34(8)：1879-1885.

［7］ Hestenes M R，Stiefel E. Methods of conjugate gradients for solving linear systems[J]. Journal of Research of the National Bureau of Standards，1952，49(6)：409-436.

［8］ Dai Y H，Kou C X. A nonlinear conjugate gradient algorithm with an optimal property and an improved Wolfe line search[J]. SIAM Journal on Optimization，2013，23(1)：296-320.

［9］ 邓娟，王妍，吕靖华，等. 三种EIT算法重建图像评价的仿真研究[J]. 医疗卫生装备，2010，31(5)：1-3，7.

［10］ 陈晓艳，李宏英，赵秋红，等. 3D-EIT系统电极优化设计[J]. 中国生物医学工程学报，2014，33(2)：155-160.

［11］ Adler A，Arnold J H，Bayford R，et al. GREIT：A unified approach to 2D linear EIT reconstruction of lung images [J]. Physiological Measurement，2009，30(6)：S35-S55.

［12］ Adler A. EIDORS：Electrical impedance tomography and diffuse optical tomography reconstruction software [EB/OL]. [2015-03-06]. http://www.sce.carleton.ca/ faculty/adler/eidors/index.shtml.

责任编辑：常涛

Parameter Selection Method of EIT Algorithm Based on Evaluation Index

CHEN Xiaoyan，CHANG Xiaomin
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

To select the parameters of EIT algorithm objectively and accurately，a novel approach was proposed to decide the number of iterations of the conjugate gradient(CG)algorithm and the regularization factors of Tikhonov regularization(TR)algorithm．Eight evaluation criterion were employed to evaluate the performances．Firstly，we encoded CG and TR algorithms respectively based on a circle EIT forward model，and obtained the solutions of each algorithm．Secondly，according to the definition of the eight evaluation criterion，the optimal reference values of the algorithms were obtained．The iteration number of the CG algorithm is 70-80 times，and the regularization factor of TR is suggested between 0.01-0.1．Thirdly，the EIT images were reconstructed with and without the reference value and compared．The quality of the image with the reference value is more satisfactory．After modification，the proposed method provides an objective assessment for the parameter selection of the electrical impedance image reconstruction algorithm，which lays a foundation for EIT image quality evaluation system.

EIT algorithm；parameter selection；conjugate gradient method；Tikhonov regularization algorithm；evaluation criterion

TP391.9

A

1672-6510(2016)06-0064-05

10.13364/j.issn.1672-6510.20150129

2015-09-22；

2016-04-07

国家自然科学基金资助项目(61301246)；天津市自然科学基金资助项目(12JCYBJC19300)

陈晓艳（1973—），女，四川成都人，教授，cxywxr@163.com.

数字出版日期：2016−07−11；数字出版网址：http：//www.cnki.net/kcms/detail/12.1355.N.20160711.1610.006.html.