一个新分数阶混沌系统的分析与同步

李 雪，薛 薇

(天津科技大学电子信息与自动化学院，天津 300222)

一个新分数阶混沌系统的分析与同步

李 雪，薛 薇

(天津科技大学电子信息与自动化学院，天津 300222)

提出一个新的同量阶2.7阶分数阶混沌系统，基于预估-校正时域法，采用Matlab绘制了该分数阶混沌系统的相轨迹图、Lyapunov指数图和分岔图，并用数值仿真验证了该系统在一定参数变化范围内存在混沌吸引子．研究该分数阶混沌系统的同步问题，基于极点配置方法以及扩展的非线性状态观测器理论，设计了一种投影同步方案．数值仿真与理论分析的结果一致，充分验证了该同步方案的可行性和有效性．

分数阶；混沌系统；状态观测器；投影同步；数值仿真

近年来，对于混沌理论及其应用的研究已经成为了科学界的热点问题．各种新的混沌系统[1-3]不断被发现和提出，促进了学者们对混沌理论的认识，丰富和完善了混沌学的研究内容，并且提高了混沌学在图像加密、视频加密、保密通信、故障诊断等领域的实际应用能力．自1983年Mandelbort[4]提出分数维以来，分数阶微积分理论已取得了极其重大的进步．不同于整数阶微积分，分数阶微积分更注重函数的整体信息，因此在将混沌系统应用到实际工程领域时，分数阶模型比整数阶模型的应用范围更广泛，效果更明显．这一现象促使越来越多的学者开始投身于研究和认识分数阶混沌系统，例如已发现的有分数阶Rössler系统[5]、分数阶Chen系统[6]、分数阶Liu系统[7]、分数阶Lü系统[8]、分数阶广义增广Lü系统[9]等．

混沌同步是实现保密通信等混沌应用的基础．随着人们对分数阶混沌系统的认识不断深入，分数阶混沌系统的同步问题得到了越来越多的关注．目前，已提出了很多分数阶混沌系统的同步方法，诸如：线性反馈同步[10]、滑膜控制[11]、投影同步[12]、自适应同步[13]、广义同步[14]等各种同步控制方法，这些同步方法的提出对混沌在实际工程领域的应用具有重要的意义．

本文提出一个新的同量阶分数阶混沌系统，给出了该分数阶混沌系统的相轨迹图、Lyapunov指数图和分岔图等特性．在此基础上，应用状态观测器的投影同步方法对所给的新分数阶混沌系统进行了同步研究．

1 新分数阶混沌系统分析

1.1 数学模型

系统含有3个非线性项，其数学模型为

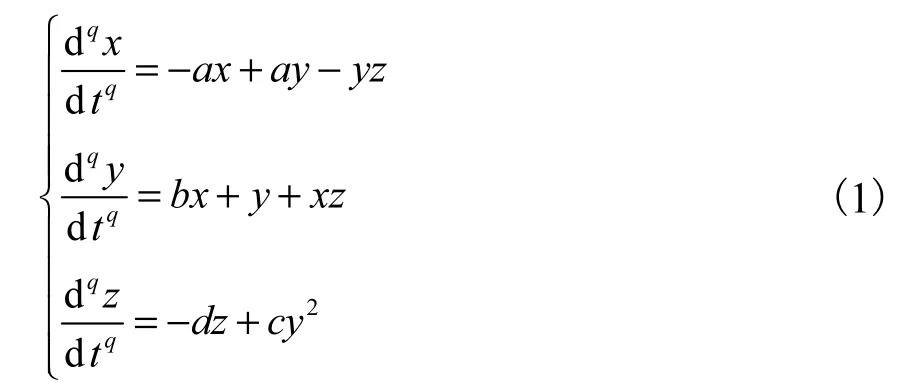
式(1)系统中各状态变量的分数阶微积分阶次为q，且q∈(0,1)，系统阶次为3q，系统参数为a, b, c, d．

1.2 分数阶次q对系统的影响

取a=34.4，b=50，c=3，d=15时，绘制式(1)系统随阶次q∈[0.7,1]变化的分岔图，如图1所示．由图1可以看出：当q∈[0.7,0.874]时，系统处于周期或者稳定状态；当q∈[0.874,1]时，系统状态解开始出现混乱现象，说明系统处于混沌状态．

图1 q∈[0.7,1]时式(1)系统在x轴上的分岔图Fig. 1 Bifurcation diagram of system(1) on x axis when q∈[0.7,1]

1.3 相轨迹分析

为了方便观察式(1)系统的混沌特性，本文选取分数阶次q=0.9时的情况进行分析．当a=34.4，b=50，c=3，d=15，q=0.9时，绘制出2.7阶系统的相轨迹图如图2所示．从图2中可以观察到式(1)系统的混沌吸引子具有丰富的几何形状和复杂的拉伸轨线．

1.4 Lyapunov指数及分岔图

这里分析2.7阶系统随参数a变化时，系统的Lyapunov指数变化和分岔情况．固定参数b=50，c=3，d=15，当a∈[20,60]时，绘制式(1)系统的Lyapunov指数图和分岔图，分别见图3和图4．

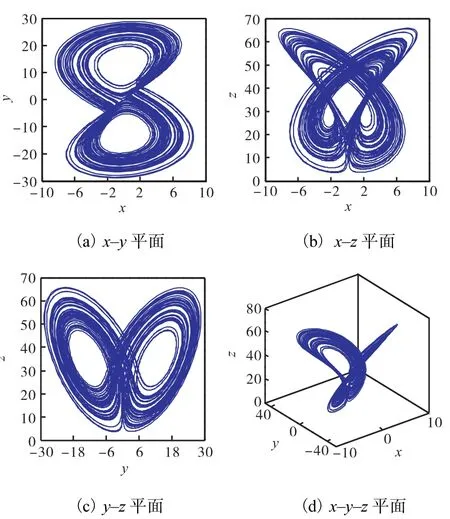
图2 式(1)系统的相轨迹图Fig. 2 Phase trajectory diagrams of system(1)

图3 a∈[20,60]时式(1)系统的Lyapunov指数谱图Fig. 3Lyapunov exponent diagram of system (1) when a∈[20,60]

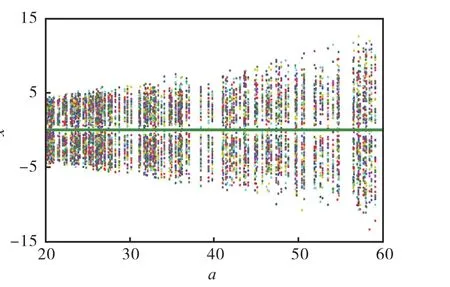
图4 a∈[20,60]时式(1)系统在x方向上的分岔图Fig. 4Bifurcation diagram of system(1)on x axis when a∈[20,60]

由图3和图4可以看出，系统随参数a变化的分岔图与其对应的Lyapunov指数谱图保持一致．当参数a=34.4时，该系统的3个Lyapunov指数分别为λ1=6.4295，λ2=−0.215 2，λ3=−54.6645．其最大LE指数比目前很多分数阶混沌系统的最大LE指数都大，如2.7阶Chen系统[6](λ1=2.397 5)、2.7阶Liu系统[7](λ1=0.0158)等．一般情况下，混沌系统的LE指数越大，其混沌特性越明显，混沌程度越高．因此，本文提出的2.7阶系统在图像加密、保密通信等方面应该会有较好的应用前景．

2 同步控制器的设计

考虑如下两个分数阶混沌系统：

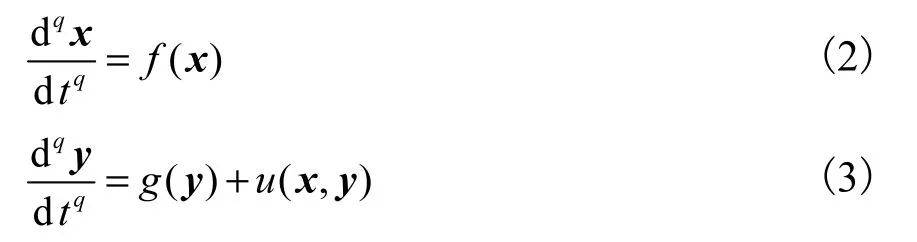
式中：状态变量为x=(x12, x2,…,x)T∈Rn和y=(y1, y2,…,yn)T∈Rn；连续向量函数为f:Rn→Rn和g∶Rn→Rn；控制器为u( x, y)．令式(2)和式(3)系统分别为驱动系统和响应系统．

定义1[15]假设∃α，且α≠0，使得式(2)系统和式(3)系统满足则称以上两个系统获得了投影同步，其中α为状态比例因子，为范数运算．

假设驱动系统为

式中：A∈Rn×n为Jacobian矩阵；B∈Rn×m为系数矩阵；F( x)为非线性项．响应系统(分数阶状态观测器)满足

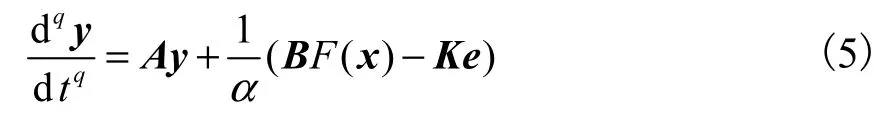
定义同步误差为e=αy−x，则误差系统为

其中K∈Rn×n为误差反馈增益矩阵．若矩阵(A−K)的特征值为负数，由分数阶线性系统的稳定性理论可知，当时，有，则驱动系统和响应系统获得了投影同步．

依据控制理论中的极点配置方法[16]适当地选取反馈增益矩阵K，使得矩阵(A−K)的特征值为负数，即可实现驱动系统和响应系统的投影同步．

以本文所提出的新分数阶混沌系统为例，令驱动系统为

将驱动系统转化为式(4)的形式，得到

响应系统可以构造成

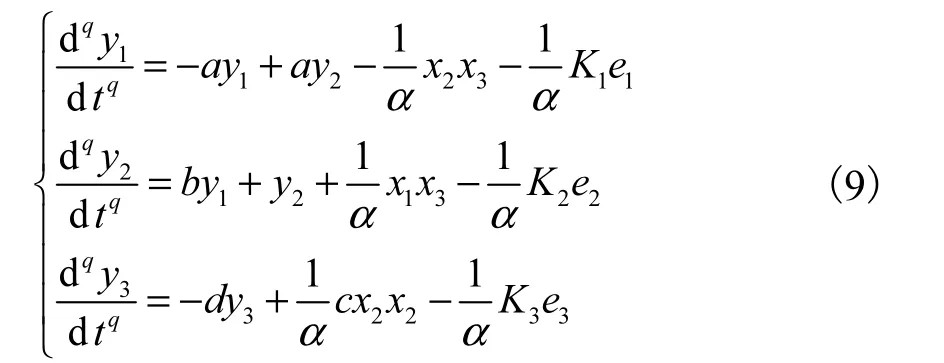
将响应系统转化为式(5)的形式，得到

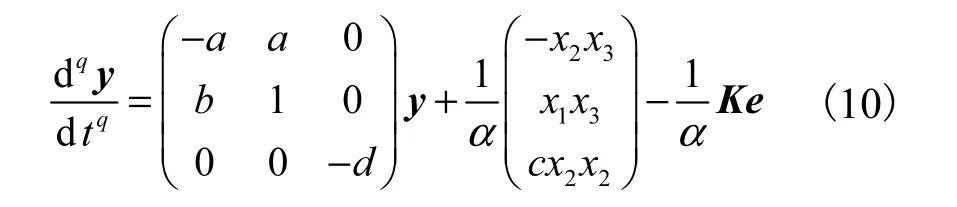
将式(8)和式(10)代入式(6)，可得

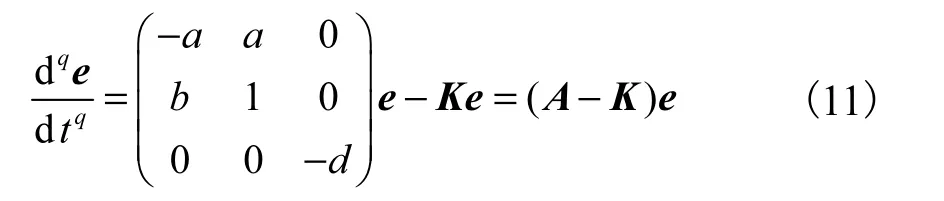
其中a＝34.4，b＝50，c＝3，d＝15，则系数矩阵A为

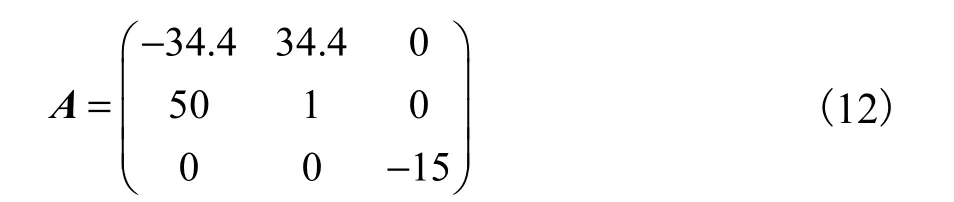
可见矩阵(A, I)可控，并且(I, AI,…,An−1I )是满秩的．依据极点配置法选取反馈增益矩阵K为

将式(12)和式(13)代入式(11)，可得到误差系统为

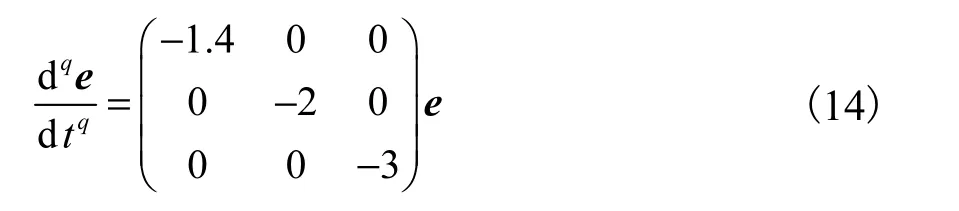
由于矩阵(A−K)的特征值为λ1=−1.5，λ2=−2，λ3=−3，也就是所有的特征值λi(i =1,2,3)全为负数．根据分数阶线性系统的稳定性理论，可以得到即式(7)驱动系统和式(9)响应系统实现了投影同步．

3 同步仿真

运用预估-校正法进行数值仿真，选取的参数a=34.4，b=50，c=3，d=15，比例因子α=1，时间步长h=0.01，驱动系统和响应系统的初始值分别为x1(0)=−1，x2(0)=−2，x3(0)=−2，y1(0)=−1，y2(0)=−2，y3(0)=3，得到的数值仿真结果如图5和图6所示．由图5可知，随着时间的增加，驱动系统和响应系统状态变量的运动轨迹完全一致．由图6可以看出，误差e1( t)、e2( t)、e3( t)可以在较短时间内渐近稳定于零，进一步说明该同步方法是可行的．

图5 同步曲线图Fig. 5 The synchronization curve

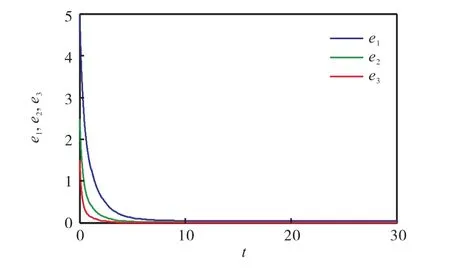
图6 同步误差随时间的变化Fig. 6 Synchronization errors versus time

4 结 语

本文提出了一个新的分数阶混沌系统，并对该系统的混沌特性进行了分析，运用Matlab软件绘制了该2.7阶新混沌系统的相轨迹图、Lyapunov指数图和分岔图．数值仿真结果表明，该系统在较大参数变化范围内存在混沌吸引子．在此基础上，研究了该分数阶混沌系统的同步问题，设计了一种投影同步方案，该同步方案依据极点配置法选取合适的反馈增益矩阵并对状态比例因子进行简单控制，所需的同步代价较小并且同步时间较短，具有一定的普遍性．通过理论分析和数值仿真充分验证了该同步方法的可行性和有效性，为该分数阶混沌系统在保密通信、图像加密等实际工程中的进一步应用提供了技术支持．

［1］ Liu C X，Liu T，Liu L，et al. A new chaotic attractor[J]. Chaos，Solitons and Fractals，2004，22(5)：1031-1038.

［2］ Qi G Y，Du S Z，Chen G R，et al. On a 4-dimensional chaotic system[J]. Chaos，Solitons and Fractals，2005，23(3)：1671-82.

［3］ 仓诗建，陈增强，袁著祉. 一个新四维非自治混沌系统的分析与电路实现[J]. 物理学报，2008，57(3)：1493-1501.

［4］ Mandelbrot B B. The Fractal Geometry of Nature[M]. New York：W H Freeman，1983.

［5］ Li C G，Chen G R. Chaos and hyperchaos in the fractional order Rössler equations[J]. Physica A，2004，341(2)：55-61.

［6］ 邵永晖，钟启龙，郑永爱. 基于分数阶Chen系统的图像加密新算法[J]. 科学技术与工程，2014，14(2)：159-164.

［7］ 陈向荣，刘崇新，王发强，等. 分数阶Liu混沌系统及其电路实验的研究与控制[J]. 物理学报，2008，57(3)：1416-1422.

［8］ Lu J G. Chaotic dynamics of the fractional order Lü system and its synchronization[J]. Physics Letters A，2006，354(4)：305-311.

［9］ Xue W，Xu J K，Cang S J，et al. Synchronization of the fractional-order generalized augmented Lü system and its circuit implementation[J]. Chinese Physics B，2014，23(6)：82-89.

［10］ Yassen M T. Controlling chaos and synchronization for new chaotic system using linear feedback control[J]. Chaos，Solitons and Fractals，2005，26(3)：913-920.

［11］ Yau H T，Yan J J. Desgn of sliding mode controller for Lorenz chaotic system with nonlinear input[J]. Chaos，Solitons and Fractals，2004，19(4)：891-898.

［12］ Wang X Y，He Y J. Projective synchronization of fractional order chaotic system based on linear separation [J]. Physics Letters A，2008，372(4)：435-441.

［13］ Yassen M T. Adaptive chaos control and synchronization for uncertain new chaotic dynamical system[J]. Physics Letters A，2006，350(1/2)：36-43.

［14］ Wang T S，Wang X Y. Generalized synchronization of fractional order hyperchaotic lorenz system[J]. Modern Physics Letters B，2009，23(17)：2167-2178.

［15］ 王兴元. 混沌系统的同步及在保密通信中的应用[M].北京：科学出版社，2012：320-330.

［16］ Paraskevopoulos P N. Modern Control Engineering[M]. New York：Marcal Dekker，2002.

责任编辑：常涛

Analysis and Synchronization of a Novel Fractional-order Chaotic System

LI Xue，XUE Wei
(College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China)

In this research，a novel commensurate 2.7-order fractional-order chaotic system is proposed．The phase trajectory diagrams，the Lyapunov exponent spectra，and the bifurcation diagrams of the fractional-order chaotic system were establisher by using Matlab software and based on the predictor-corrector time domain method．The results imply there exists a chaotic attractor in the system with a certain range of change in system parameters．On this basis，the synchronization of the fractional-order chaotic system was investigated and a projection synchronization scheme based on the pole assignment method and the extended nonlinear state observer theory was designed．The simulation results are consistent with the theoretical analysis，which further demonstrates the feasibility and effectiveness of the proposed synchronization scheme.

fractional-order；chaotic system；state observer；projection synchronization；numerical simulation

TP391.9

A

1672-6510(2016)06-0069-05

10.13364/j.issn.1672-6510.20160004

2016-01-05；

2016-07-08

国家自然科学基金青年科学基金资助项目(11202148)

李 雪（1991—），女，河北人，硕士研究生；

薛 薇，教授，xuewei@tust.edu.cn.