数学思考：让数学教学回归本原

周海荣

回归本原的价值审思

2011年12月28日，义务教育数学课程标准修订稿出台，随后，各大版本数学实验教材也相继修订并推广使用，这在一定程度表明，义务教育数学课程改革进入到一个新的阶段。向学科本身回归，是这一阶段比较鲜明的特征。也就是说，数学课要更加具有“数学味”，数学学习要能充分地显示出数学学科的育人价值。

这种回归可以看成是对前一阶段数学课程改革的修正。《人民教育》记者李帆曾发表过这样的评论：“从本世纪初伊始的新课程改革，到2010年《教育规划纲要》颁布，十年间，基础教育经历了一场深刻的思想和观念的洗礼，选择、多元、个性，人人耳熟能详。然而，观念难落地！”（《人民教育》2014第22期）个人以为，“难以落地”的重要表现之一就在人们对新课程理念始终处在接纳、领悟、理解和实践摸索阶段，其间走了不少弯路，遭遇到很多阻力。有一段时间，形式化、浅表化的东西充斥着课堂，数学课上得不像数学课了，数学课应该承载的学科价值和育人价值被削弱了。

这种回归可以看成是对我国学校教育形态的顺应和遵从。长期以来，我国基础教育阶段的学校教育都是分学科进行的，学科教学是学校教育的基本形态——通过一门门学科的学习，让学生获得不同的学科知识、能力、素养，并最终汇聚成人的全面发展。也就是说，学好每一门学科，是培育全面发展的人的前提和基础。数学，作为小学生学习的主要课程之一，其价值和功能是毋庸置疑的，应该给以重视，不折不扣地加以落实。

这种回归还可以看成是对数学学科特有的育人价值的充分肯定。学生为什么每天都要坐在教室里上数学课？老师到底为了什么而给孩子上数学课？数学学习对一个人的成长到底产生着什么样的影响？这些看似形而上的问题，恰恰是数学教学最本原的问题。要回答这些问题，就得思考数学这门学科具有怎样的特点，数学学习过程中这些特点是如何得以呈现，被学习者感受，又如何在思考、思维乃至智慧生长方面发挥作用等。把这些想清楚了，数学教学的品质就不一样了。

总之，向学科本身回归，就是要慎重而全面地考量数学学习对儿童所产生的深刻影响，充分发挥好数学学科的育人价值。这是数学学习的本真意义，也是数学学科的价值所在。

在回归中超越

追求“数学思考”的理性把握是数学课堂教学的必然归宿，也是数学教育价值的根本体现。怎样才能在教学中实践“数学思考”的教学追求呢？我们将通过几个教学案例，从数学自身的整体性、逻辑性、理性特点，谈谈在课堂教学中对“数学思考”理性把握的实践。

◎一、数学的整体与结构化思维

数学学科的重要特点之一就是思维的整体性、结构性。数学学习，既要注重知识的“生长点”，也要关注思维的“链接点”。从日常的每节课或每个单元来看，每一个知识点可能是分散的、琐碎的，这样的教学造成了儿童认知结构的脱节和割裂，所以学习要站在系统的高度，运用结构化思维，将看似分散的知识点，集成一个有机的知识整体。

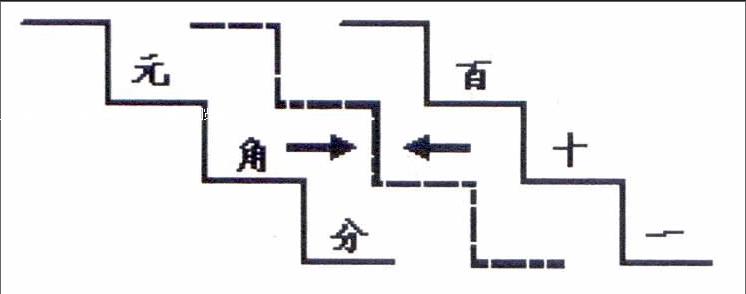
【案例】一年级下册“认识人民币”教学片段（P66、67）：

师：学完这一节课，我们已经认识了哪些人民币单位？

生：元、角、分。

师：（出示）这是一个1分的硬币，1分1分地往上加，加到10分就产生一个新的单位，就是——

生：角。

师：如果1角1角地往上加，加到10角，又产生了一个大一些的单位——

生：元。

师：这里有一个台阶，你能把这三个人民币单位按照一定的顺序摆放在上面吗？（生说过程，师课件操作。）

师：刚才数的过程，与之前学习的认数有什么相同的地方？

生1：数数的时候，也是一个一个地数，数满十个一就是1个十，数满10个十就是1个百。

生2：老师刚才数钱的时候，一个一个地往上加，就好像摆小棒，一根一根地摆，摆满10根就捆成一捆；然后再一捆一捆地摆，摆满10捆，就再捆成一个大捆。

师：我们也可以把一、十、百这三个计数单位放在台阶图上。谁来试一试？

师：这两个不同的单位之间有什么相同的地方？

生：都是满十进一。

师：正因为它们都是满十进一，所以我们可以把这两个台阶合二为一。虽然它们代表的单位不一样，但相邻两个单位之间的关系都是10。这样的一个关系，在以后我们认识更大的数、学习其他的单位时还会遇到。

《义务教育数学课程标准（2011版）》开篇即说：“数学是研究数量关系和空间形式的科学。”这句话点出了数学学科的本质：关系。在这个案例中，从纵向角度分析，将元、角、分这三个人民币单位用相邻两个单位之间的进率是10的关系建立起台阶图；从横向角度分析，将使用中的货币单位与计数中的计数单位进行比较，融通了计数单位和货币单位的“十进制”关系，让学生深刻体会到数学知识间的联系。这样的处理，不仅帮助学生加深对货币单位之间关系的理解，还融通数学内部联系，体现出数学知识的结构性。进而让学生获得融会贯通的酣畅，豁然开朗的喜悦，自主建构的兴奋，应用自如的徜徉，让数学学习也成为他们快乐的生命之旅！

◎二、数学的逻辑与联系性思维

数学是一门逻辑性很强的学科。小学数学的内容虽然多数比较简单，其中不少内容是描述性的，但内容的编排上仍体现着前后的连贯性和很强的逻辑性。在平时的课堂教学中，我们同样需要通过联系性思维，来开启学生的心智，让他们好好地学习小学数学这门学科。我们都知道，对于知识的学习和掌握是来源于学生的好奇心。只有让他们对于某个知识产生了好奇心，才能让他们对这个知识产生兴趣，从而去学习、去研究其中的奥秘。

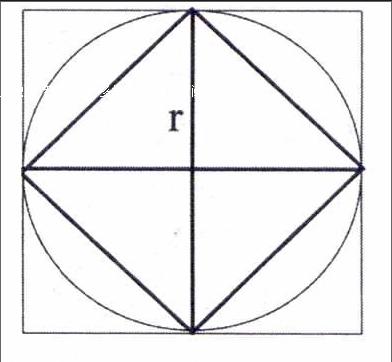
【案例】五年级下册“圆的面积”教学片段（P96、97）：

师：刚才，我们以圆的半径r为边长画一个小正方形和一个大正方形，得出小正方形的面积是2r2，大正方形的面积是4r2。猜测一下圆的面积大约是多少？

生：大约是3r2。

师：回想一下，以前我们推导新图形的面积公式，是怎么做的？

生：转化成已经学过的图形。比如平行四边形沿它的一条高剪开，可以拼成长方形。

师：这种转化的方法很不错，能不能顺着这个思路，把圆也转化成学过的图形呢？请小组讨论，再动手剪一剪、拼一拼。

师：（学生演示：将圆平均分成4份）这个图形有点像什么图形？

生：平行四边形。

师：有一点点像，但还不太像，能想办法使它更像一点吗？

……

师：通过刚才的操作，你发现了什么？

生：平均分的份数越多，拼成的图形就越像平行四边形。

师：我们把圆平均分成4份，拼成的图形有点像平行四边形；平均分成8份，像多了；平均分成16份，更像了；平均分成32份，拼成的图形开始趋向于长方形。请大家闭上眼睛想象，如果把圆平均分成64份、128份、256份……随着等分的份数越多，拼出的图形最终会转化成什么图形？

生：长方形。

【导学单】：（1）拼成的长方形的面积与圆的面积有什么关系？

（2）长方形的长与圆的周长有什么关系？宽与圆的半径呢？

（3）思考：圆的面积应该怎样计算？

……

师：通过推导，得出圆的面积就是r2的π倍，这和开始推导出圆的面积在4r2和2r2之间是吻合的。

对事物本质的认识，是数学思考的核心。从生活化的情境到数学化的过程，是学生数学学习的重要过程，也是数学理性发展的重要逻辑。在本案例中，从学生熟悉的正方形面积入手，提供给学生思考、想象、猜测的机会，体会图形转化的前后联系，渗透数学思想方法于整个教学过程，使学生充分体会到数学思之有“据”、思之有“理”、思之有“序”。从繁杂到简单，学生在追求简约化的数学学习中，感受到转化思想的精髓。这不仅是让学生在解决问题中学会数学思考，更是让学生在对生活现象的反思之中运用数学的思想方法，厘清本质，使整个学习过程“数学化”，数学素养得到培养和升华。

◎三、数学的理性与批判性思维

首都师范大学王尚志教师说：“数学要讲逻辑推理，更要讲道理。”理性是数学特有的气质，数学理性也是数学文化的一个重要内涵。数学思维的训练、数学思想的感悟、数学活动经验的积累，都离不开数学理性的参与。而小学生的思维以感性为主，如何让感性的小学生撩起神秘的理性面纱，让抽象的数学学习更接“地气”，让数学学习不能停留在知道“是什么”，还要明白“为什么”，这就需要寻求从形象到抽象的思维路径。对“为什么”的追问可以看成是培养学生理性思维的一个方面。

【案例】五年级上册“小数乘小数”教学片段（P64、65）：

师：同学们，刚才我们用竖式来计算1.15×3.2的小数乘小数。请同学们回想一下，我们在计算小数加减法的时候，写竖式要注意什么对齐？

生：小数点和小数点对齐，也就是相同数位对齐。

师：为什么在小数加减法中是相同数位对齐，而在小数乘法里又是末位对齐呢？数学上为什么要这样规定？

（学生茫然）

师：我们把1.15×3.2分开来算，1.15×0.2等于多少？（0.230）1.15×3等于多少？（3.45）按照数位把它们写出来应该是什么样子？（学生写）

相同数位对齐： 末位对齐：

师：观察我们按照相同数位对齐的格式写出的竖式，你有什么想说的？

生1：算结果是简单的，但是把这个结果写到竖式里比较麻烦。

生2：特别要注意小数点的位置，一不小心就会错。

师：对比这两种书写的格式，你有什么想说的？

生3：在算的过程中，我们都是把它们当成整数进行计算的。

生4：相同数位对齐的写法，比较麻烦，特别是写竖式时要注意小数点的位置，容易错。

生5：第二种书写格式，和我们之前学习的整数乘法是一样的，只要在最后的得数里点上小数点就行了。

生6：末位对齐的书写格式，比较整齐、方便。

师：同学们，小数乘法末位对齐的这种书写格式，它不仅是一个数学规定，更是数学追求方便、简洁的一种思考。

数学学习为每一个认识、理解、逻辑、思考都提供一种可行的注解，是数学理性能力的重要表现。许多数学规定在历经丰富的过程后，逐渐变得简约，约定俗成了。然而在现实的教学中，教师往往用“数学规定”一言以蔽之。从学习的角度来看，“冰冷的美丽”背后一定有“火热的思考”，这种思考可以和前人发现数学规律的经历一致，可以和知识的结构脉络一致，也可以和儿童特有的经验一致。但不管怎样，都是为了学生能更好地理解数学，学好数学。上述案例书写格式的探讨，借助对比的感性认识，让学生对“末位对齐”的这个“数学规定”有了进一步理性思考，最终建立起自己的数学理解、数学认识、数学逻辑和数学思考。

“数学是思维的体操。”学生能够理性地思考，才能生长出数学智慧；学生能够自主地感悟，才能够具有生命的意义。唯有从数学学科本质出发，向学生展现数学的独特魅力，学生才能从中获取智慧的启迪、素养的滋润和生长的力量！