余能原理基面力元法在桁架大变形分析中的应用

任 聪，李瑞雪，单岩岩，彭一江

(北京工业大学建筑工程学院，北京 100124)



余能原理基面力元法在桁架大变形分析中的应用

任 聪，李瑞雪，单岩岩，彭一江

(北京工业大学建筑工程学院，北京 100124)

为了对桁架弹性大变形问题进行针对性研究，对平面二维问题的基面力单元模型进行了改进，把平面四边形四边中节点基面力单元退化为平面二节点桁架基面力单元，推导了桁架大变形余能原理控制方程和单元轴力、节点位移表达式，根据由控制方程得出的桁架大变形问题的非线性方程组，利用Matlab语言编制了基面力元程序，计算了桁架结构几何非线性算例。与大型通用有限元软件ANSYS的计算结果进行了对比分析，所用方法的结果与理论解一致，与ANSYS的计算结果相差较小。因此可得结论：所介绍的基面力元模型是可靠的，可以应用于对桁架结构的几何非线性问题分析，具有较广阔的前景。

弹性力学；基面力元法；余能原理；桁架；弹性大变形

随着高强、轻质、弹性好的合成材料相关研究的不断发展进步，柔性杆件已经在很多工程结构中被广泛应用。经典的小变形理论已不能满足建筑结构的需求，人们越来越多的将研究工作重点放在了杆件弹性大变形的研究工作中。有限元法作为研究工程结构力学的重要数值方法之一，近些年来随着计算机技术水平的提高，取得了显著的进步。但是传统的有限元法均是以二阶应力张量作为描述体系，在这种理论框架下，建立和表述弹性大变形问题的数学模型较为复杂繁琐，高度非线性，适用性较差。

GAO[1-2]提出了“基面力”的概念，给出了弹性大变形问题新的描述方法，利用基面力可以较简洁地完全描述一点的应力状态，为研究弹性大变形问题提供了一个良好的分析工具。在高玉臣[3]提出的基面力理论体系基础上，彭一江等[4-9]进行了基于基面力概念的新型有限元方法“基面力元法”的研究工作，推导了适用于弹性大变形余能原理大位移、大转动问题基面力元法模型，把基面力元法应用到了弹性大变形有限元问题的分析中。经过近几年的研究，余能原理基面力元法在弹性大变形问题的研究取得了一些成果[10-13]。

本文以余能原理基面力元法理论为基础，针对桁架结构弹性大变形问题，推导了对应的余能原理基面力桁架单元模型，并利用Matlab语言编制了有限元程序，验证了该模型的适用性。

1 弹性大变形问题的余能原理基面力元法

1.1 基面力的二维表示

对于二维平面问题，分别用P，Q来表示物质变形前后的径矢，用xα(α=1,2)来表示Lagrange随体坐标，则对每个点可以建立以下2种标架：

(1)

为了描述一点Q的应力状态，在向量dx1Q1,dx2Q2上作一个平行四边形微元,将基线力定义为

(2)

式中：dx3=dx1；dTα为第α边上的合力。

1.2 基面力的平面二节点桁架单元

如图1所示为传统的具有平面四边中节点平面四边形基面力元法有限元单元[14]。当单元足够小时，假设应力均匀地分布在每一个边上，I，J分别表示平面4节点单元的第I个边和第J个边,且I，J=1,2,3,4；TI，TJ为作用在第I个边和第J个边中点上面力的合力，简称为单元面力。

本文把基面力元法四边形单元退化为平面二节点桁架单元，如图2所示。I，J分别表示单元的第I个边和第J个边,且I，J=1,2。

图1 平面4节点的单元Fig.1 Four-nodes plane element

图2 平面2节点桁架单元Fig.2 Two-nodes plane truss element

以基线力作为基本未知量，物质余能密度可表示为

(3)

式中：W为变形前的应变能密度；AP为变形前的基面；uα为位移梯度。

(4)

根据式(3)和式(4)，可将余能密度分为变形和转动两部分

(5)

单元余能变形部分的具体表达式为

(6)

式中：A0为单元的面积；pI,J为I边和J边边中节点变形前径矢PI和PJ的点积；MI为第I边边中点的径矢，其表达式为

MI=MPI。

(7)

式中：M为由PI到MI的转动张量，对平面单元其表达式为

(8)

单元余能转动部分的具体表达式为

(9)

式中：U为单位张量。

1.3 修正的余能原理

设桁架结构存在n个桁架单元，则余能原理有限元的支配方程是下列系统泛函的约束极值问题：

(10)

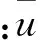
单元的余能泛函可用单元面力T和单元转角θ组成的显式来表示：

(11)

利用Lagrange乘子法，放松平衡条件约束，则修正后的单元余能泛函可以表示为

(12)

式中λ=[λ1,λ2]为Lagrange乘子。

则系统的修正泛函为单元的修正泛函总和

(13)

由修正的余能原理可得，系统泛函的驻值条件写为

(14)

由式(14)可以得到系统关于未知量单元面力T单元转角θ，以及单元拉格朗日乘子λ组成的控制方程的一组非线性方程组：

(15)

对单元之间的面力协调约束条件，传统的基面力单元只有2个面相交，交点处共用一个节点号，利用编程，分别赋予两单元接触面以大小相等、方向相反的单元面力T和-T即可。但对于桁架结构的基面力元法杆单元来说，多个杆单元交于一个点，显然是不适用的。

本文利用编程，根据单元节点处力的平衡条件∑Tα=0，对于n根杆交于一点处的情况，赋予n-1个相应单元的节点编号，通过程序自动生成n-1个节点号相应的控制方程元素，使这一约束条件得到满足。求解上述非线性方程组，即可得到各单元的面力T。

1.4 轴力及位移表达式

在求出单元面力T后，各单元应力可由式(16)计算:

(16)

式中：TI为平面节点桁架单元第I边上的单元面力；QI为变形后单元第I边边中节点的径矢；AQ为变形后的单元面积。

由于桁架单元受单向应力状态，一点的主应力仅有一个非零，则其轴向应力表达式为

(17)

轴力表达式为

(18)

式中A为桁架的横截面面积。

平面单元的边中节点位移可通过各单元的支配方程求得，其公式可写为

(19)

节点位移的显式表达式可写为

MI-PI+λ。

(20)

2 数值算例

2.1 算例1

如图3所示的平面2单元桁架，为方便研究，取各杆的刚度均为EA=10 000 N，泊松比v=0。在单元的交点处作用一个大小为1 000 N竖向集中力P。通过Matlab程序计算得出各单元轴力和各节点位移解(BFEM解)与运用ANSYS有限元软件建模计算进行了对比分析，结果如表1和表2所示。

图3 平面2单元桁架Fig.3 Two plane elements of truss

单元号轴力/NBFEMANSYS理论解线性12000.01995.72000.01666.72-1176.5-1173.2-1176.5-1333.3

由表1和表2可得该算例的Matlab程序计算结果与该问题的理论解吻合[15]，与ANSYS计算结果相比误差较小，结果具有较高的精度。

表2 节点位移

根据计算结果可知，该桁架结构弹性大变形与线性弹性变形的节点位移、轴力相差较大。图4为结构的变形图，其中位置A为本文的几何非线性解，位置B是线性变形解。

图4 桁架结构变形图Fig.4 Map of the deformation of the truss structure

2.2 算例2

计算条件：如图5所示的平面14单元桁架，为方便研究，取各杆的刚度均为EA=10 000 N，泊松比v=0。在单元节点5处作用一个大小200 N竖直向下的集中力P。通过Matlab程序计算得出各单元轴力和各节点位移(BFEM解)，与运用ANSYS有限元软件建模计算进行了对比分析，结果如表3和表4所示。

图5 平面5单元桁架Fig.5 Five plane elements of the truss

单元号轴力/NBFEMANSYS1-450.1230-450.13562-468.3929-468.39293-432.6308-432.64644-393.8450-393.88065441.4040441.44986436.1052436.15297410.8765410.8940单元号轴力/NBFEMANSYS8410.9600410.97469-14.3509-14.359710-18.6855-18.68671128.435128.417712-74.2537-74.227313-13.4145-13.456714-114.1244-114.1370

表4 节点位移

由计算结果可得该算例的Matlab程序计算与ANSYS计算结果相比误差较小，具有较高的精度。

图6所示为该桁架结构的几何非线性变形图。

图6 桁架结构变形图Fig.6 Map of the deformation of the truss structure

3 结 论

与传统的位移模式有限元相比，本文介绍的桁架结构大变形分析余能原理基面力元模型具有简洁的表达形式，有利于应用软件进行编程计算。给出的桁架结构几何非线性基面力元分析方法的结果与理论解一致，与ANSYS有限元软件的非线性解相差较小，具有较高精度和收敛性，具有较好的计算性能。以基面力为基础建立的桁架结构几何非线性分析基面力元模型具有良好的适用性，可以用于分析各种类型的复杂桁架结构问题。

[1] GAO Yuchen. Large deformation field near a crack tip in rubber-like material[J]．Theoretical and Applied Fracture Mechanics，1997，26(3)：155-162．

[2] GAO Yuchen. A new description of the stress state at a point with applications[J]. Archive of Applied Mechanics，2003，73(3)：171-183．

[3] 高玉臣. 固体力学基础[M]. 北京: 中国铁道出版社, 1999.

[4] 彭一江.基于基面力概念的新型有限元方法[D].北京:北京交通大学,2006. PENG Yijiang. A New Finite Element Based on the Base Forces[D].Beijing:Beijing Jiaotong University,2006.

[5] PENG Yijiang,LIU Yinghua. Base force element method of complementary energy principle for large rotation problems[J].Acta Mechanica Sinica,2009,25(4):507-515.

[6] PENG Yijiang, DOGN Zhanlong, PENG Bo,et al. The application of 2D base force element method (BFEM) to geometrically non-linear analysis[J].International Journal of Non-Linear Mechanics，2012,47(3):153-161.

[7] PENG Yijiang, PU Jiwei, PENG Bo, et al. Two-dimensional model of base force element method (BFEM) on complementary energy principle for geometrically nonlinear problems[J]. Finite Elements in Analysis and Design，2013, 75: 78-84.

[8] PENG Yijiang, GUO Qing, ZHANG Zhaofeng,et al. Application of base force element method on complementary energy principle to rock mechanics problems[J].Mathematical Problems in Engineering,2015, 2015:1-16.

[9] LIU Yinghua，PENG Yijiang, ZHANG Lijuan, et al. A 4-mid-node plane model of base force element method on complementary energy principle[J]. Mathematical Problems in Engineering，2013,2013:1-8.

[10]彭一江，刘应华．基面力概念在几何非线性余能有限元中的应用[J]．力学学报,2008, 40(4): 496-501. PENG Yijiang,LIU Yinghua.Application of the base forces concept in geometrically nonlinear finite element method on complementary energy[J].Chinese Journal of Theoretical and Applied Mechanics,2008, 40(4): 496-501.

[11]彭一江，刘应华．基于余能原理的有限变形问题有限元列式[J]．计算力学学报,2009，26(4)：460-465. PENG Yijiang， LIU Yinghua. Finite element formulation for finite deformation problem based on complementary energy principle[J]. Chinese Journal of Computational Mechanics,2009，26(4)：460-465.

[12]LIU Yinghua，PENG Yijiang．Base force element method(BFEM) on complementary energy principle for linear elasticity problem[J].Science China Physics，Mechanics and Astronomy，2011，54(11)：2025-2032．

[13]张昭锋，彭一江，郭庆，等.余能原理基面力元法在重力坝应力分析中的应用[J].河北工业科技,2014,31(5):425-428. ZHANG Zhaofeng, PENG Yijiang, GUO Qing,et al.Application of complementary energy principle based base force element method in stress analysis of gravity dam[J].Hebei Journal of Industrial Science and Technology,2014,31(5):425-428.

[14]PENG Yijiang, DONG Zhanlong, PENG Bo,et al. The application of 2D base force element method (BFEM) to geometrically non-linear analysis[J]. International Journal of Non-Linear Mechanics，2012, 47(3): 153-161.

[15]徐友良.桁架结构大变形问题的位置解法[J].工程力学，2010,27(sup1)：43-47. XU Youliang.Location vector method to solve the large deformation of truss structure[J].Engineering Mechanics, 2010,27(sup1):43-47.

Application of base force element method on complementary energy principle in large deformation analysis of the truss

REN Cong, LI Ruixue, SHAN Yanyan, PENG Yijiang

(College of Civil and Engineering，Beijing University of Technology，Beijing 100124，China)

In order to pointedly research the large elastic deformation problems of the truss, the model of the plane base force element method is improved. The plane 4-side 4-node base force element is degenerated into the 2-node truss element. The governing equations of the BFEM for large elastic deformation of truss, the expressions of the axial force and the displacements formulation of nodal point are derived. According to the system of nonlinear equations for the large elastic deformation problems of the truss obtained by the governing equations, the base force element program is developed by MATLAB technology. The typical numerical examples of the truss in geometric nonlinearity are calculated. The result is compared with that calculated by the ANSYS finite element software. It shows that the result of the proposed method is in accordance with the theoretical solution, and the difference between the result and that calculated by ANSYS is little. So the conclusion can be made that the model of BFEM given in this paper is reliable, and it can be used for geometric non-linear analysis of truss structure with wide application extension.

elastic mechanics；base force element method; complementary energy principle; truss; large elastic deformation

1008-1534(2016)04-0288-05

2016-04-12;

2016-05-12；责任编辑：陈书欣

国家自然科学基金(10972015)

任 聪(1990—)，男，河北保定人，硕士研究生，主要从事余能原理基面力元法方面的研究。

彭一江教授，博士生导师。 E-mail:pengyijiang@bjut.edu.cn

O343

A

10.7535/hbgykj.2016yx04004

任 聪，李瑞雪，单岩岩，等.余能原理基面力元法在桁架大变形分析中的应用[J].河北工业科技,2016,33(4):288-292. REN Cong, LI Ruixue, SHAN Yanyan,et al. Application of base force element method on complementary energy principle in large deformation analysis of the truss[J].Hebei Journal of Industrial Science and Technology,2016,33(4):288-292.