基于模糊理论的汽车冷凝器PFMEA改进

张佳栋，夏蓓鑫

(上海大学机电与自动化工程学院，上海 200072)

基于模糊理论的汽车冷凝器PFMEA改进

张佳栋，夏蓓鑫

(上海大学机电与自动化工程学院，上海 200072)

为了解决传统PFMEA中RPN分析存在的分辨率和准确性不高的问题，提出一种利用权重赋予法和模糊分析的综合评价方法。通过引入专家组构建评价指标的判断矩阵，基于一致性检验及算术平均法计算得到各评价指标的权重，以提高RPN的分辨率；综合考虑评价指标权重集对指标的模糊评价矩阵的影响，赋予专家组的模糊评价矩阵不同的权重，以量化不确定的主观判断因素。研究结果表明：在汽车空调冷凝器制造PFMEA中出现工序RPN值相同和其风险顺序不能反映实际情况的问题时，该综合评价方法能够对工序风险程度进行正确排序，加强了PFMEA对风险控制和预判的作用。

机械制造工艺与设备其他学科；PFMEA；汽车空调冷凝器；风险顺序；RPN；模糊分析

作为一种风险评估工具，PFMEA主要应用于生产制造过程，是一种识别生产过程中失效潜在影响的重要方法[1]。管理者可以通过PFMEA实现风险排序，进而将有限的资源投入到最高风险的控制措施中，从而有效降低整个过程风险[2-3]。传统的PFMEA一般使用RPN来确定风险顺序，其中RPN=严重度(S，Severity)×发生频度(O，Occurrence)×探测度(D，Detectability)[4]。

随着市场竞争动态化、全球化和用户驱动的趋势加剧，制造业所面临的挑战也越来越严峻，PFMEA的作用开始凸显[5]。然而，使用RPN来衡量风险的传统PFMEA方法暴露出一系列问题[6-7]。其中一个重要问题是在一些情况下RPN值无法表征风险顺序，具体包括：当RPN值相同时，无法判断应当优先采取哪一项措施；RPN值越大并不意味着优先采取措施。例如在汽车空调冷凝器生产PFMEA中有A和B两道工序，A钎焊工序的RPN为90，严重度为9，B氦检工序的RPN为112，严重度为7。在这样的情况下，即使B工序的RPN值比A工序的高，也不能确定是否应该对B工序先采取措施，因为A钎焊工序是全铝式冷凝器制造过程中的核心工序[8]。另一个重要问题是，传统风险分析的过程带有很强的主观判断，如有时小组成员在评定风险时试图通过设定一个较低的数值来降低RPN值[9]。这种行为虽然可以使措施的工作量减少，但是会使产品的风险大大增加。

鉴于以上情况，本文提出模糊综合评价方法以解决上述问题。模糊综合评价方法的优点在于能对信息呈现模糊性的资料作出比较科学、合理、贴近实际的量化评价[10]。因此，根据该方法，在综合考虑严重度、发生频度、探测度差异的基础上，通过引入专家组，量化专家组的主观因素，并对结论进行评分来确定风险优先级别[11]，从而加强PFMEA对风险控制和预判的作用。

1 模糊综合评价法的PFMEA分析

1.1 收集PFMEA数据

收集PFMEA数据，建立PFMEA表格，这些数据应该包括：

1) 潜在的产品失效模式，是指过程中可能出现的不满足设计要求和性能的问题点；

2) 潜在的后果，是指失效模式对产品质量可能引发的不良影响；

3)潜在的失效原因，是指失效是怎样引起的，针对每个潜在的失效模式列出尽可能多的失效原因；

4) 现行控制的方式，是指在当前过程中，尽可能防止失效模式发生的控制方法的描述；

5) 风险顺序，是指该项特性对于产品性能影响的严重程度。

1.2OSD权重评估

成立专家小组，对评价指标严重度(S)、发生频度(O)、探测度(D)进行比较分析，建立判断矩阵，行、列按照O，S，D3个元素排列，可通过表1选取O，S，D之间的比较数值Vij，其中用整数表示前者和后者比的重要程度，倒数表示后者和前者比的重要程度[12]。

表1 O，S，D比较数值

注：*选取数值2，4，6，8表示介于上述比较程度之间。

式(1)是第i个专家对O，S，D的判断矩阵

(1)

对判断矩阵Zi进行一致性检验，要求CR<0.1，否则需要对判断矩阵进行修正，直到通过一致性检验。

CR=CI/RI，

(2)

1.3 确立各权重值

设评价指标权重向量为A，

A=(a1a2… an) 。

(3)

使用算术平均法对判断矩阵Zi的每列进行平整化处理，分别得到O，S，D的权重分配[13]

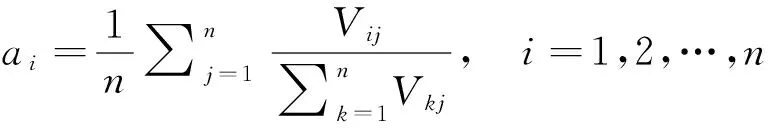
(4)

1.4 建立模糊评价矩阵

首先对各工序中的失效因素的评价指标给予不同的评价等级Vj，让专家组对各项指标进行评定，设V为评价等级集，它包含j个由专家组对指标的主观评定信息的评分结果。

V={V1,V2,…,Vj} 。

(5)

一般取j=5，即极低、较低、一般、较高、极高5级评价等级：

V={V1,V2,V3,V4,V5}={极低，较低，一般，较高，极高} 。

(6)

然后由专家组对项目中的失效因素依据O，S，D3个指标进行打分，用Vij表示对第i项指标的第j级评价等级，再计算出不同评价等级在各项指标评价等级中的比例，用rij表示

(7)

最后，将上述专家组的主观评价信息汇总，建立指标的模糊评价矩阵[14]

(8)

1.5 模糊综合评价

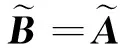
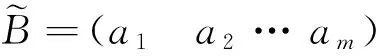
(b1b2…bn)。

(9)

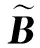
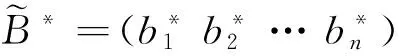
(10)

为了方便风险顺序的排序，设M为模糊评价结论等级值，再建立等级矩阵C，矩阵中包含n项等级的评分数值，将模糊评价矩阵B点乘等级矩阵C的转置矩阵，赋值后即得到结论等级值M：

C=(C1C2…Cn) ，

(11)

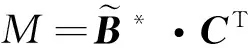
(12)

2 模糊综合评价法的PFMEA应用

根据以上分析，以某汽车空调制造商为例[15]，按照客户和TS16949要求制作冷凝器产品的PFMEA，如表2所示。

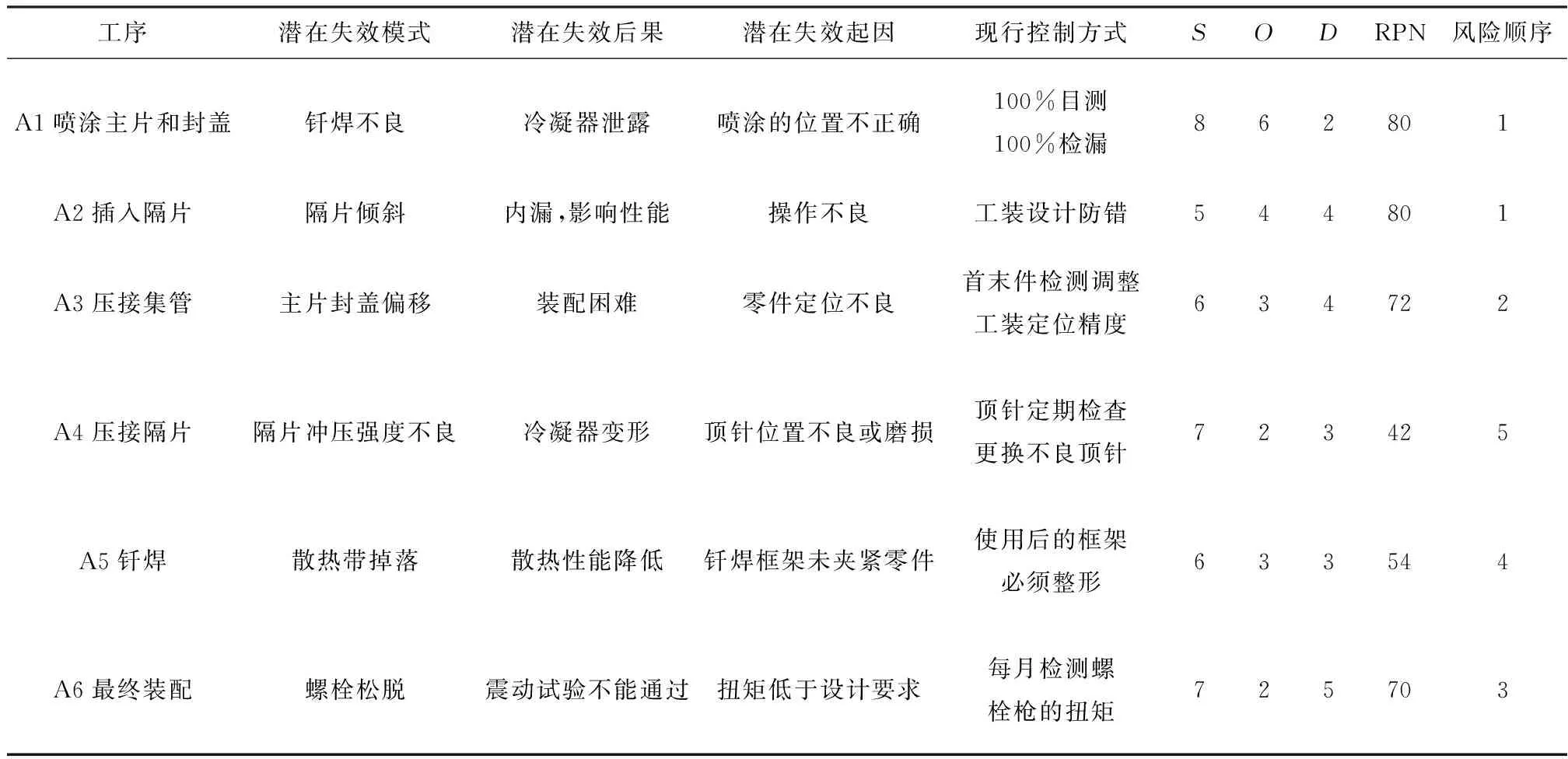
表2 冷凝器PFMEA

在该传统的PFMEA表中存在2个问题。其一，存在A1工序和A2工序RPN值相同的情况。难以区分采取措施的优先顺序。其二，存在不合理的情况。以A3工序和A5工序为例，两者只在D上稍有偏差，使得A3工序比A5工序的RPN值高，但是A3工序的失效不会对冷凝器的性能有任何影响，而A5工序的失效则会使冷凝器性能下降。

现在使用模糊综合评价法对表2中工序的风险进行重新排序。

1)建立项目专家小组，小组成员由质量经理、工艺经理、生产经理、项目工艺工程师、产品工程师、现场生产工程师组成，对表2中的评价指标O，S，D进行权重评估，根据评价结果建立判断矩阵，见表3。

使用算术平均法计算每个专家的O，S，D权重矩阵Z，见表4。

对6个专家的权重结果进行平均化，得到权重向量A=(0.149 9 0.663 2 0.187 0)

专家组对失效模式从O，S，D3方面进行等级评价，见表5。

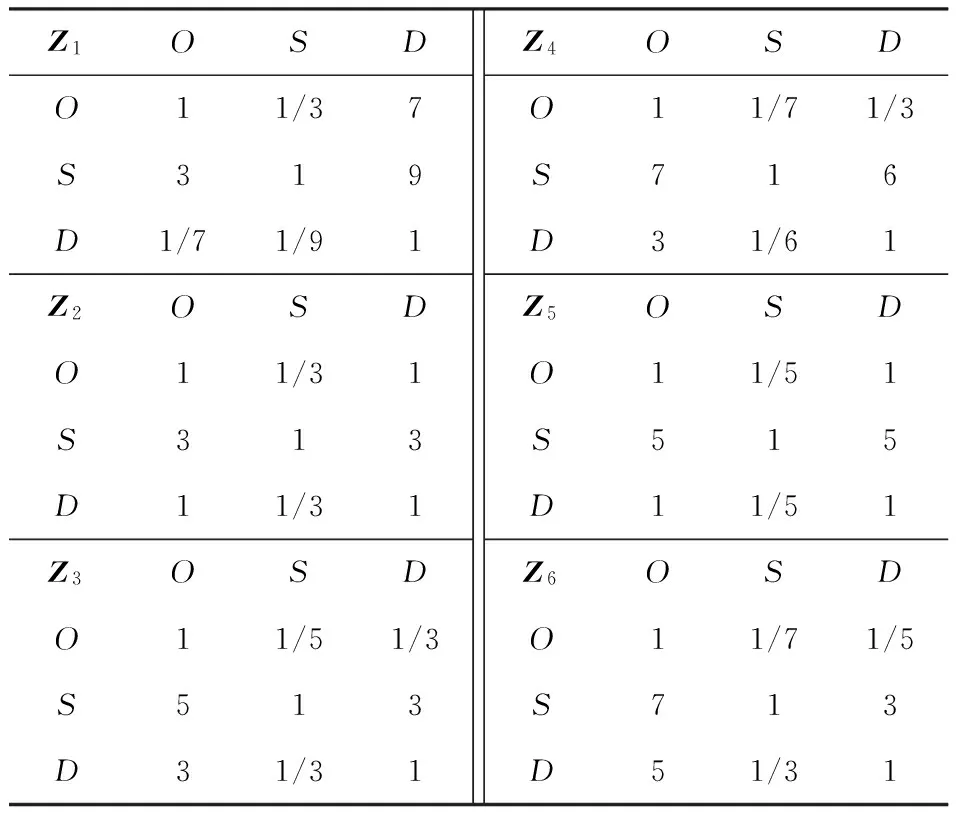
表3 O，S，D判断矩阵

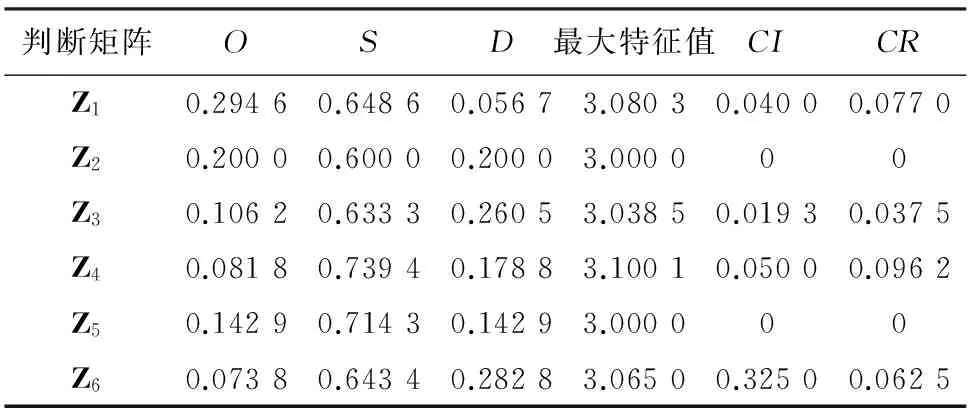
表4 O，S，D权重矩阵

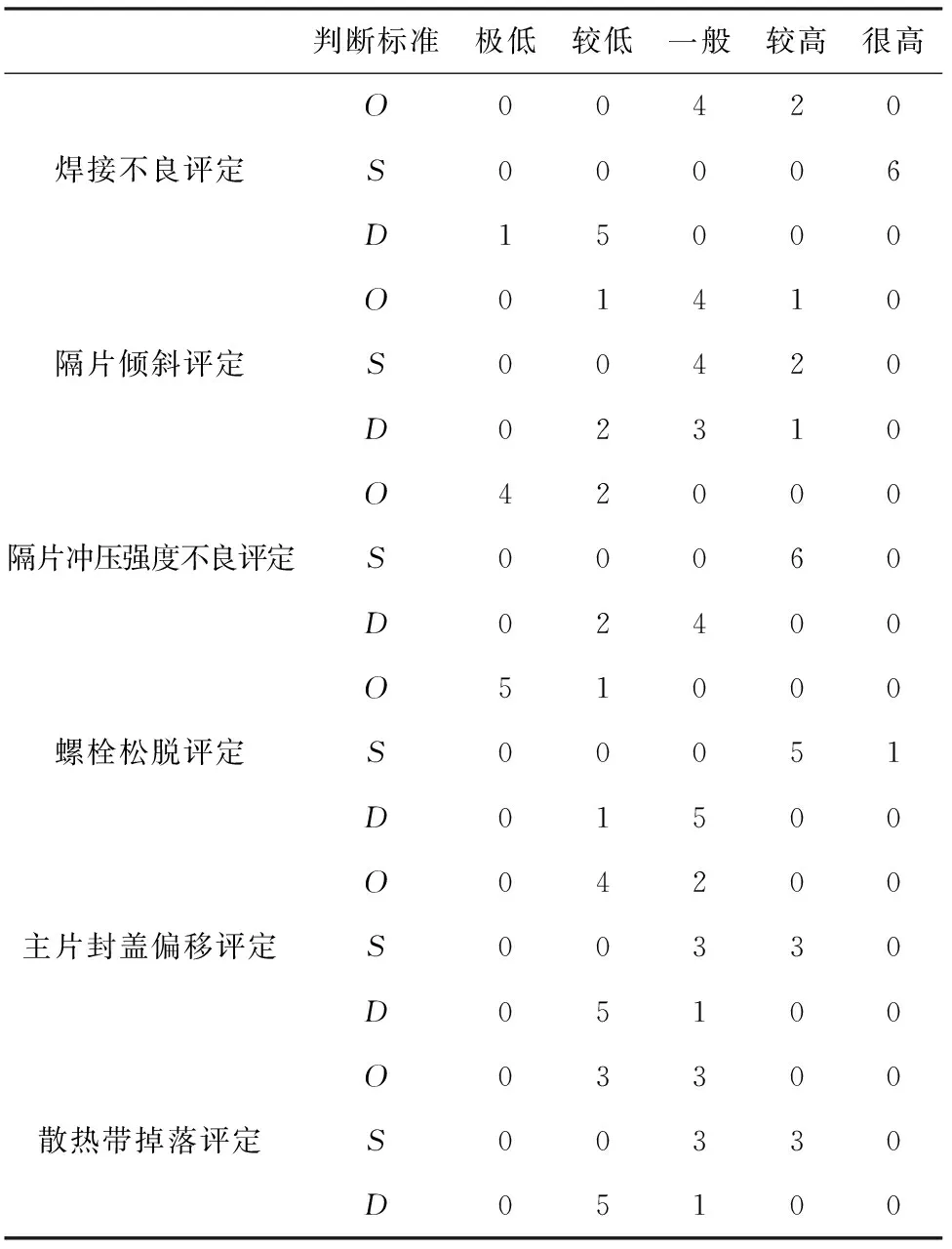
表5 等级评价矩阵

统计各等级评分数量在评分总量上所占的比例，建立如下模糊评价矩阵。

分别与权重矩阵A相乘，得到如下每个工序风险的模糊评价。

B1=[0.03 0.16 0.1 0.05 0.66] ，

B2=[0 0.09 0.64 0.27 0]，

B3=[0 0.26 0.41 0.33 0] ，

B4=[0.10 0.11 0.13 0.11 0.55] ，

B5=[0 0.23 0.44 0.33 0] ，

B6=[0.12 0.06 0.16 0.55 0.11]。

利用等级矩阵C=[1 2 3 4 5]对以上模糊评价赋值，得到等级值M：

M1=4.15；M2=3.18；M3=3.07；M4=3.90；M5=3.10；M6=3.47。

汇总以上数据见表6，发现与传统的RPN分析法相比，使用该方法得到结论等级值M都是不相同的，符合实际情况。

根据表6数据绘制帕累托图(见图1)，可以看到A1，A4，A6，A2工序的失效频率占总失效频率的70%以上，是产品失效的主要原因，应当优先采取措施预防风险。

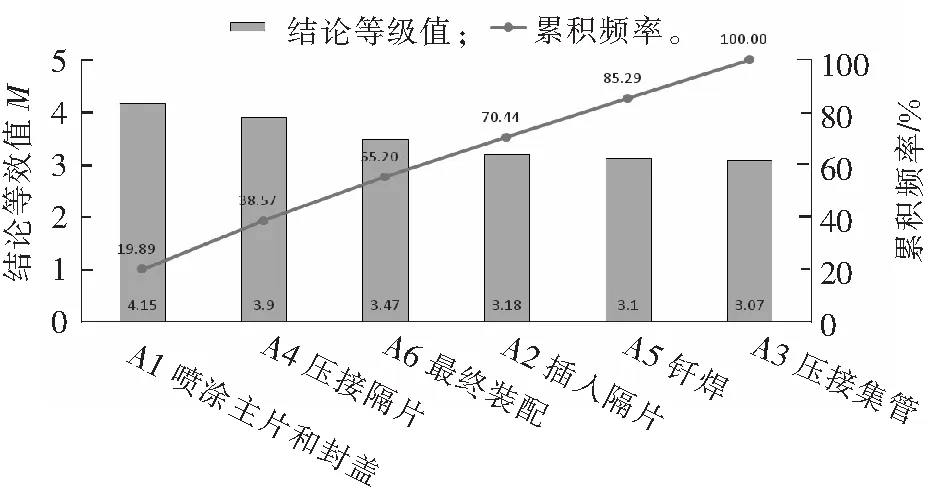
图1 工序失效帕累托图Fig.1 Process failure Pareto diagram

3 结 论

改进后的PFMEA方法一方面利用O，S，D权重赋予法，通过专家组的评价矩阵、一致性检验及算术平均法确定评价矩阵的权重，从而将RPN中3项指标的差异因素凸显出来，提高了RPN值的分辨率；另一方面引入模糊理论，综合考虑评价指标权重集对指标的模糊评价矩阵的影响，进而赋予专家组的模糊评价矩阵不同的权重，从而大幅降低以往PFMEA方法中专家组存在的主观判断问题，提升了RPN值的准确性。汽车空调冷凝器制造的实例验证表明该PFMEA在实际应用中能发挥更大作用。

[1] 王绍印.故障模式和影响分析(FMEA)[M].广州:中山大学出版社,2003.

[2] CHANG C L, WEI C C, LEE Y H. Failure mode and effects analysis using fuzzy method and grey theory[J]. Kybernetes,1999, 28: 1072-1080.

[3] 邓慧琼, 徐刚, 张颖. 考虑隐性故障时电网二级连锁过载的风险水平分析方法研究[J]. 河北科技大学学报, 2014, 35(2):164-171. DENG Huiqiong, XU Gang, ZHANG Ying. Researchon risk level analysis method of cascading overload in power grid with two stages considering recessive faults[J]. Journal of Hebei University of Science and Technology, 2014, 35(2): 164-171.

[4] AMBEKAR S B, EDLABADKAR A, SHROUTY V. A Review: Implementation of failure mode and effect analysis[J]. International Journal of Engineering and Innovative Technology, 2013, 2(8): 37-41.

[5] 王雷, 李震, 刘志虎，等. 基于信息素的制造系统动态协调研究[J]. 河北科技大学学报, 2014, 35(4):318-323. WANG Lei, LI Zhen, LIU Zhihu, et al. Research on pheromone-based dynamic coordination for manufacturing system[J]. Journal of Hebei University of Science and Technology, 2014, 35(4): 318-323.

[6]DINMOHAMMADI F, SHAFIEE M. A fuzzy-FMEA risk assessment approach for offshore wind turbines[J]. International Journal of Prognostics and Health Management, 2013,4: 1-10.

[7]SELLAPPAN N, PALANIKUMAR K. Modified prioritization methodology for risk priority number in failure mode and effect analysis[J]. International Journal of Applied Science and Technology,2013, 3(4): 27-36.

[8]蒋金龙.汽车铝热交换器的真空钎焊[J].焊接技术,1999(2): 8-10. JIANG Jinlong. Vacuum brazing of aluminum heat exchangers for automotive[J]. Welding Technology, 1999(2): 8-10.

[9]奚立峰,徐刚.FMEA在过程管理中的应用[J].工业工程与管理,2002(1):37-39. XI Lifeng, XU Gang. Application of FMEA in process management[J]. Industrial Engineering and Management, 2002(1):37-39.

[11]杨伦标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,1993.

[12]任玉辉,肖羽堂. 层次分析法在校园火灾危险性分析中的应用[J].安全与环境工程,2008, 15(1): 85-88. REN Yuhui, XIAO Yutang. Application of analytic hierarchy process to the campus fire hazard analysis[J]. Safety and Environmental Engineering, 2008, 15(1): 85-88.

[13]李荣钧,邝英强.运筹学[M].广州:华南理工大学出版社,2002.

[14]熊启才.数学建模方法及应用[M].重庆:重庆大学出版社,2005.

[15]张蕾.汽车空调[M].北京:机械工业出版社,2007.

Improvement of PFMEA for automobile condenser based on fuzzy theory

ZHANG Jiadong, XIA Beixin

(School of Electrical Engineering and Automation, Shanghai University, Shanghai 200072, China)

Aiming at the problems of low resolution and low accuracy of RPN(risk priority number) analysis in traditional PFMEA (process failure mode and effects analysis), a comprehensive evaluation method based on weight given and fuzz analysis techniques is proposed. Expert group is introduced to establish judgment matrix of evaluation indexes, then the weights are calculated based on consistency check and arithmetic method to improve the resolution of RPN. The effect of weight set on fuzzy judgment matrix is overall considered, and the fuzzy judgment matrixes of the expert group are assigned with different weights to quantize uncertain subjective factors. The results indicate that the proposed method can correctly sort the degrees of process risks when process RPN value is equal or the risk order cannot reflect actual condition in automobile air conditioning condenser, which strengthens the PFMEA’s abilities in risk control and prognosis.

other discipline of manufacturing processes and equipment; PFMEA; automobile air conditioning condenser; risk order; RPN; fuzz analysis

1008-1534(2016)04-0324-05

2016-03-15;

2016-04-01；责任编辑：冯 民

国家自然科学基金(71401098)；上海市高校青年教师培养资助计划项目(ZZSD15047)

张佳栋(1985—)，男，上海人，硕士研究生，主要从事风险控制方面的研究。

夏蓓鑫博士，讲师。E-mail: bxxia@shu.edu.cn

TH165.3

A

10.7535/hbgykj.2016yx04011

张佳栋，夏蓓鑫.基于模糊理论的汽车冷凝器PFMEA改进[J].河北工业科技,2016,33(4):324-328. ZHANG Jiadong, XIA Beixin.Improvement of PFMEA for automobile condenser based on fuzzy theory[J].Hebei Journal of Industrial Science and Technology,2016,33(4):324-328.