水平井双管注聚合理配注量的优化方法

孙 哲，孙 巍，曾 晟，万庆生

(1.东北石油大学提高油气采收率教育部重点实验室，黑龙江大庆 163318；2. 中国石油集团工程设计有限责任公司北京分公司，北京 100000；3. 中国石油大庆油田有限责任公司储运销售分公司，黑龙江大庆 163000)



水平井双管注聚合理配注量的优化方法

孙 哲1，孙 巍1，曾 晟2，万庆生3

(1.东北石油大学提高油气采收率教育部重点实验室，黑龙江大庆 163318；2. 中国石油集团工程设计有限责任公司北京分公司，北京 100000；3. 中国石油大庆油田有限责任公司储运销售分公司，黑龙江大庆 163000)

为研究水平井配注量问题，以聚合物波及效率最大为目标函数，以注入井、生产井的井底流压为约束条件，建立了水平井注聚-直井采油混合井网水平井双管注聚合理配注量优化的数学模型，给出了辽河油田水驱高246块高2-莲H16水平井的合理配注量。结果表明，根据上述方法计算出的水平井的合理配注量与油田实际配注量基本吻合，验证了此方法的正确性。

渗流力学；水平井与直井；水平井双管注聚；合理配注量；优化方法

近年来，人们在水平井渗流理论分析方面取得了许多研究成果。美国的JOSHI[1]利用电场流理论，假定水平井泄油体是以水平井两端点为焦点的椭圆体，将三维渗流问题简化为垂直及水平渐内的二维间题，利用势能理论详细推导了均质油藏水平井产能公式；郎兆新等[2]用一种形式简单的茹可夫斯基函数作变换，获得了压力分布、产量计算、见水时间及面积扫油系数公式；曲德斌等[3]应用复位势理论及迭加原理研究典型的开发井网——一般的水平井五点法面积井网，其中包括产量、见水时间、波及系数的计算以及流函数的导出等；胡军晖等[4]综述了水平井产能的4种计算方法，并给出了当储层存在渗透率各向异性、井偏心或地层损害时修正的产能计算公式；尹洪军等[5]建立了非均质气藏水平井三维渗流产能预测的数学模型，采用有限元方法对其进行求解；于金萍[6]应用复位势理论及叠加原理对水平井注水-直井采油井组、直井注水-水平井和直井采油井组进行了研究，给出了这两个典型井组水井合理配注量的确定方法。

目前，研究水平井合理配注量的优化方法多是基于水驱的，对于水平井注聚合理配注量优化的问题考虑的较少。水平井可以增大油藏泄油面积，提高注剂的注入速度和波及效率，水平井结合聚合物驱油技术可以提高原油采收率，改善油田开发效果。因此，对于水平井注聚合理配注量优化的研究具有十分重要的实际意义。

1 数学模型

1.1 油层压力场分布

假设无限大地层一个混合井网中1口水平井双管注聚，周围有n口直井采油，供给边界处的压力为pe，注聚水平井水平段长度为2l，地层平均渗透率为K，平均有效厚度为h。

1)基本关系式

在Zo平面建立以注聚水平井外管的水平段轴线为xo轴，其水平段中点为坐标原点o的直角坐标系(xo,yo)。在Zi平面建立以注聚水平井内管的水平段轴线为xi轴，其水平段中点为坐标原点o的直角坐标系(xi,yi)。第i口生产井在Zo平面和Zi平面的坐标转换关系为

xii=xoi-l ，

(1)

yii=yoi。

(2)

应用儒可夫斯基保角变换将真实平面上的复杂流动问题变换为像平面上的单向流动问题。第i口生产井在真实平面和像平面的坐标转换关系为

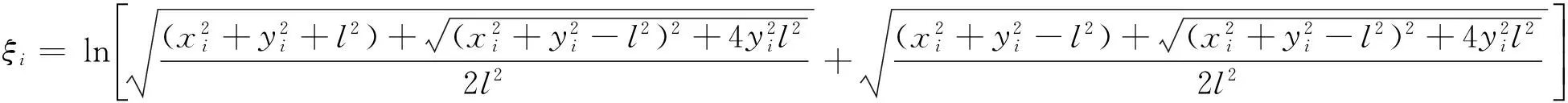
(3)

(4)

式中：(xii,yii)为第i口生产井在Zi平面下的坐标；(xoi,yoi)为第i口生产井在Zo平面下的坐标；l为注聚水平井水平段长度的1/2，m；(ξi,ηi)为第i口生产井在像平面下的坐标；(xi,yi)为第i口生产井在真实平面下的坐标。

2)油层压力场分布函数

根据镜像理论及势的叠加原理，推导出水平井与直井混合井网油层压力场分布函数为

(5)

由式(5)可得第i口生产井井底流压pwfi为

(6)

其中

(7)

(8)

(9)

(10)

(11)

式中：μs为聚合物溶液在地层中渗流时的剪切黏度，Pa·s；Qoi为第i口生产井受注聚水平井外管注聚驱替的产量，m3·s-1；(ξoi,ηoi)为第i口生产井经保角变换后在外管像平面下的坐标；K为地层渗透率，m2；h为油层的有效厚度，m；Qii为第i口生产井受注聚水平井内管注聚驱替的产量，m3·s-1；(ξii,ηii)为第i口生产井经保角变换后在内管像平面下的坐标；C为常数，可通过供给边界处的势确定，m2·s-1；ρowi为第i口生产井在外管像平面上的半径，m；ρiwi为第i口生产井在内管像平面上的半径，m；k为稠度系数，Pa·sn；n为流性指数，无因次；υ为渗流速度，m/s；c′为与毛细管迂曲度有关的系数，其变化范围是25/12～2.5；φ为地层孔隙度，无因次；rwi为第i口生产井在W平面下的半径，m；Qho为注聚水平井外管注入量，m3·s-1；Qhi为注聚水平井内管注入量，m3·s-1。

1.2 目标函数

目标函数是聚合物波及效率最大，即

(12)

其中

(13)

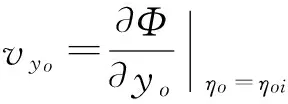
(14)

(15)

(16)

式中：toi为注入聚合物由注聚水平井外管的井壁沿主流线到达第i口生产井井底的时间，s；tii为注入聚合物由注聚水平井内管的井壁沿主流线到达第i口生产井井底的时间，s；A为井网面积，m2；vyo为任意一点从注聚水平井的外管到生产井的主流线上沿yo方向的渗流速度，m·s-1；vyi为任意一点从注聚水平井的内管到生产井的主流线上沿yi方向的渗流速度，m·s-1。

1.3 约束条件

约束条件为

pR≤piwf≤piwfmax，

(17)

其中

piwfmax=pf(1-X),

(18)

pf=HmY，

(19)

piwfmin=pp+0.01γm(Hm-Hp) ，

(20)

式中：pR为目前地层压力，MPa；piwfmax为最大合理注聚井井底流压，MPa；pf为地层破裂压力，MPa；X为破裂概率，无因次；Hm为油层中部深度，m；Y为破裂压力梯度，MPa·m-1；piwfmin为最小合理生产井井底流压，MPa；pp为合理泵口压力，MPa；γm为生产井井筒内混合液相对密度，无因次；Hp为泵挂深度，m。

2 优化方法

1)输入水平井双管注聚-直井采油井组的基础数据：N，A，h，K，φ，n，k，Hm，pR，Y，2l，piwfmax，Zo，(xoi,yoi)，rwi，γm，Hp，pwf；

2)由式(7)计算聚合物溶液在地层中渗流时的剪切黏度μs；

3)由式(1)—式(4)计算直井生产井在外管、内管像平面下对应的直角坐标(ξoi,ηoi)、(ξii,ηii)；

4)由式(18)计算注聚水平井的最大合理井底流压piwfmax，由式(20)计算直井生产井的最小合理井底流压piwfmin；

5)在保证注聚水平井外、内管注入聚合物的推进速度vξ1i和vξ2i相同的条件下，由式(6)计算各直井生产井的产量Qoi和Qii；

6)由(10)计算注聚水平井外管注入量Qho，由式(11)计算注聚水平井内管注入量Qhi；

7)由式(7)计算波及效率Ea；

8)判断Eamax

9)piwf=piwf+1，判断式(17)，若成立，则转至步骤(5)，反之，则转至步骤(10)；

10)由式(12)可知，波及效率Eamax=max{Ea}，与此对应的注聚水平井外管注入量Qho、内管注入量Qhi为最优外管注入量Qoo、内管注入量Qio。

3 计算实例

根据上述水平井与直井混合井网水平井双管注聚合理配注量的优化方法，计算辽河油田水驱高246块高2-莲H16水平井双管注水时的合理配注量。

如图1所示，高246块高2-莲H16水平注水井周围有10口与其连通的直井生产井。含油面积A为1.31km2，平均油层有效厚度h为38.1m，油层平均渗透率k为0.588μm2，孔隙度φ为0.218，油层中部深度Hm为1 560m，高2-莲H16水平注水井外管水平段长度2lo为120.98m，内管水平段长度2li为222.12m。

图1 高246块高2-莲H16井位图Fig.1 Well location map of G2-H16 in G246 Block

应用上述优化方法计算的辽河油田水驱高246块高2-莲H16水平井注水量与波及效率的关系如图2所示。

图2 高246块高2-莲H16井注水量与波及效率关系Fig.2 Relationship between injection volume and sweep efficiency of G2-H16 in G246 Block

图2表明，当外管注水量为27m3/d，内管注水量为46m3/d时，波及效率较高。辽河油田水驱高246块高2-莲H16水平井的外管实际日配注量为28m3/d，内管实际日配注量为45m3/d。因此，根据上述方法计算出的水平井的合理配注量与油田实际配注量基本吻合，可以认为本文给出的水平井注聚-直井采油混合井网水平井双管注聚合理配注量的优化方法是正确的。

4 结 语

建立了水平井注聚-直井采油混合井网水平井双管注聚合理配注量优化的数学模型，给出了这种混合井网水平井外、内管合理配注量的优化方法。对辽河油田水驱高246块高2-莲H16水平井的应用分析表明，根据上述方法计算出的水平井的合理配注量与油田实际配注量基本吻合，验证了本文数学模型及优化方法的正确性。研究结果为水平井与直井混合井网的渗流理论提供了重要支持，为今后研究更符合油藏中渗流实际情况的水平井数学物理模型提供了参考。

[1] JOSHI S D. A review of horizontal well and drain hole technology [C]// SPE16868.[S.l.]:[s.n.], 1988: 226-230.

[2] 郎兆新, 张丽华, 程林松, 等. 水平井与直井联合开采问题——五点法面积井网[J]. 石油大学学报(自然科学版), 1993, 17(6)：50-55. LANG Zhaoxin, ZHANG Lihua, CHENG Linsong, et al. Combined production of vertical and horizontal wells—A 5-spot well pattern[J]. Journal of the University of Petroleum, China, 1993, 17(6): 50-55.

[3] 曲德斌, 葛家理, 王德民. 水平井与直井联合面积布井的开发理论研究(一)——一般的五点面积井网[J]. 石油勘探与开发, 1995, 22(1)：35-38. QU Debin, GE Jiali, WANG Demin. Combination production of vertical and horizontal wells—5-spot well pattern [J]. Petroleum Exploration and Development, 1995, 22(1): 35-38.

[4] 胡军晖, 郡捷年. 水平井产能的影响因素[J]. 石油勘探与开发, 1994, 21(5)：44-52. HU Junhui, YAN Jienian. The factors affecting the productivity of horizontal well [J]. Petroleum Exploration and Development, 1994, 21(5): 44-52.

[5] 尹洪军, 吕杭, 蔡明, 等. 非均质气藏水平井三维渗流的产能预测方法[J]. 数学的实践与认识, 2011, 41(16)：59-64. YIN Hongjun, LYU Hang, CAI Ming, et al. Productivity prediction method of 3D seepage horizontal wells in heterogeneity gas reservoir [J]. Mathematics in Practice and Theory, 2011, 41(16): 59-64.

[6] 于金萍. 水平井与直井联合布井不规则井网水井配注量的确定方法研究[D]. 大庆：东北石油大学, 2010. YU Jingping. Study on Determination Approaches of Water Injection Rate of Skewed Pattern with a Combination of Horizontal and Vertical Wells [D]. Daqing: Northeast Petroleum University, 2010.

[7] 钟会影, 蔡明, 杨钊, 等. 考虑基岩向井筒供气的气藏压裂水平井产能预测模型[J]. 数学的实践与认识, 2014, 44(18)：132-137. ZHONG Huiying, CAI Ming, YANG Zhao, et al. Productivity prediction model for fractured horizontal wells considering the gas rate of matrix flowing into well bore [J]. Mathematics in Practice and Theory, 2014, 44(18): 132-137.

[8] TSUNEKI I, TATSUNERI D, YOJI N. Stability of oil-water emulsion with mobile surface charge[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2006, 29(1): 128-141.

[9] JONG Y K, MYUNG G S, JONG D. Zeta potential of nanobubbles generated by ultrasonication in aqueous alkyl polyglycoside solutions[J]. Journal of Colloid and Interface Science, 2000, 23(3): 285-291.

[10]王德民, 程杰成, 吴军政, 等. 聚合物驱油技术在大庆油田的应用[J]. 石油学报, 2005, 26(1)：74-78. WANG Demin, CHENG Jiecheng, WU Junzheng, et al. Application of polymer flooding technology in Daqing Oilfield[J]. Acta Petrolei Sinica, 2005, 26(1):74-78.

[11]ABOLRAZL E, ELHEM G, TORAJ M. Separation of water-in-oil emulsion using microfiltration[J]. Desalination, 2005, 185(3): 371-382.

[12]孙焕泉. 胜利油田三次采油技术的实践与认识[J]. 石油勘探与开发, 2006, 33(3)：262-266. SUN Huanquan. Practice and understanding on tertiary recovery in Shengli Oilfield[J]. Petroleum Exploration and Development, 2006, 33(3): 262-266.

[13]袁淋, 李晓平, 张璐, 等. 水平井稳态产能公式对比与分析[J]. 岩性油气藏, 2013, 25(6)：127-132. YUAN Lin, LI Xiaoping, ZHANG Lu, et al. Analysis and correlation of steady-state productivity formulas for horizontal wells[J]. Lithologic Reservoirs, 2013, 25(6): 127-132.

[14]王大为, 李晓平. 水平井产能分析理论研究进展[J]. 岩性油气藏, 2011, 23(2)：118-123. WANG Dawei, LI Xiaoping. Advances in deliverability analysis of horizontal well[J]. Lithologic Reservoirs, 2011, 23(2): 118-123.

[15]于雷, 车飞, 许磊明, 等. 水平井产能与人工裂缝参数相关性模拟实验[J]. 断块油气田, 2015, 22(2)：221-223. YU Lei, CHE Fei, XU Leiming, et al. Correlation simulation experiment of productivity and artificial fracture parameters for horizontal well[J]. Fault-Block Oil & Gas Fie1d, 2015, 22(2): 221-223.

Optimization method of rational polymer injection allocation rate for horizontal well dual pipe polymer injection

SUN Zhe1, SUN Wei1, ZENG Sheng2, WAN Qingsheng3

(1. Key Laboratory of Enhanced Oil Recovery of Ministry Education, Northeast Petroleum University, Daqing, Heilongjiang 163318, China; 2. China Petroleum Engineering Company Limited Beijing Company, Beijing 100000, China; 3. Storage and Transportation Sales Branch, Daqing Oilfield Corp PetroChina, Daqing, Heilongjiang 163000, China)

In order to study the problems of horizontal well polymer injection allocation rate, considering the maximum sweep efficiency as the object function, taking the bottom hole flowing pressure of the injection well and the production wells as the constraint conditions, the mathematical model of the optimization of the horizontal well dual pipe rational polymer injection allocation rate is established under the combined well pattern of horizontal well for polymer injection and vertical wells for oil extraction. The rational injection allocation rate of the G2-H16 horizontal well in waterflood Gao 246 Block of Liaohe Oilfield is given. The results indicate that the calculated rational injection allocation rate of the horizontal well is nearly identical to actual data in the oilfield, which proves the correctness of the method.

seepage mechanics; horizontal and vertical wells; horizontal well dual pipe polymer injection; rational polymer injection allocation rate; optimization method

1008-1534(2016)04-0319-05

2016-03-17;

2016-04-29；责任编辑：冯 民

国家自然科学基金(51574086);东北石油大学研究生创新科研项目(YJSCX2015-010NEPU)

孙 哲(1988—)，女，山东高密人，博士研究生，主要从事提高采收率技术方面的研究。

E-mail:sunzhe1988dqyt@126.com

TE357.46

A

10.7535/hbgykj.2016yx04010

孙 哲，孙 巍，曾 晟, 等.水平井双管注聚合理配注量的优化方法[J].河北工业科技,2016,33(4):319-323. SUN Zhe, SUN Wei, ZENG Sheng, et al.Optimization method of rational polymer injection allocation rate for horizontal well dual pipe polymer injection[J].Hebei Journal of Industrial Science and Technology,2016,33(4):319-323.