一道高考旧题推陈出新的精彩结论

●石向阳 (南雅中学 湖南长沙 410129)



一道高考旧题推陈出新的精彩结论

●石向阳 (南雅中学 湖南长沙 410129)

一道高考旧题，经过探索，从抛物线推广到一般常态二次曲线，得出一系列结论．结论证明的关键是平移坐标系，构造齐二次方程，再利用韦达定理与和角的正切公式，经过整理、对照得到动直线恒过定点或斜率恒为定值的结论．

平移；齐二次方程；动直线过定点；充要条件

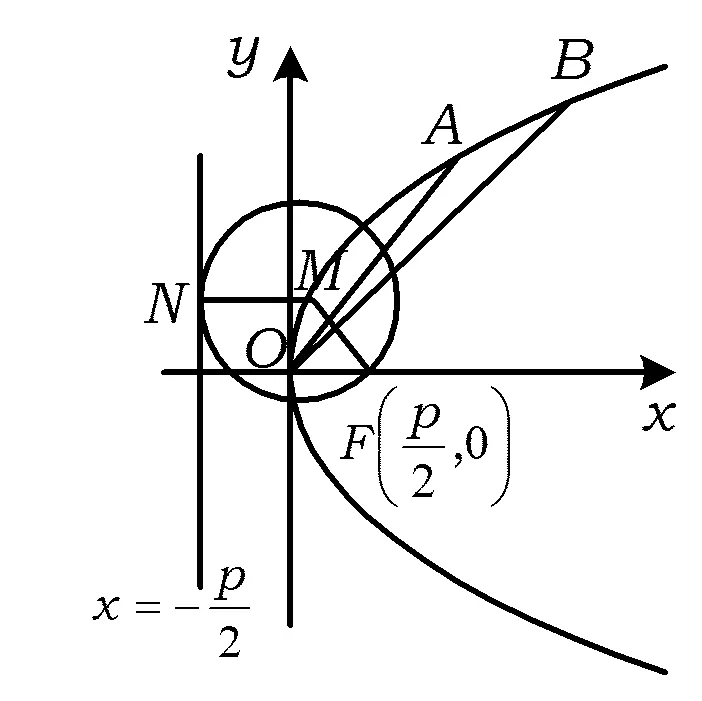
图1

1)求动圆圆心的轨迹C的方程.

2)设A,B是轨迹C上异于原点O的2个不同的点，直线OA和OB的倾斜角分别为α和β.当α,β变化且α+β为定值θ(其中0<θ<π)时，证明:直线AB恒过定点，并求出该定点的坐标．

(2005年山东省数学高考理科试题第22题)

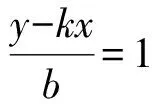
整理得

by2-2pxy+2pkx2=0.

因为x≠0，所以

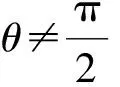
因此

此时，直线AB的方程可表示为

即

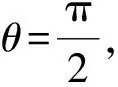
tanαtanβ=1,

即

亦即

b=2pk.

因此,直线AB的方程可表示为y=kx+2pk，即

k(x+2p)-y=0,

从而直线AB恒过定点(-2p,0).

做完该题目之后，笔者作了进一步的探索．首先把定点O改成抛物线C：y2=2px(其中p>0)上一般的定点P(x0,y0)，在上述解法的基础上增加一步平移：x′=x-x0，y′=y-y0，问题得到解决；然后，笔者把抛物线改成椭圆、双曲线，也分别得到了相应的结论；最后，笔者把结论推广到了一般常态二次曲线Ф:Ax2+Bxy+Cy2+Dx+Ey+F=0，得出一系列非常漂亮、实用的结论．

上述思维过程从特殊到一般，为了叙述的方便、简洁，笔者按照一般到特殊的思路整理如下，不当之处,请批评指正．

定理1 常态二次曲线Ф:Ax2+Bxy+Cy2+Dx+Ey+F=0上有一定点P(x0,y0)和异于点P的2个动点Q,R.设PQ的倾斜角为α，PR的倾斜角为β,则

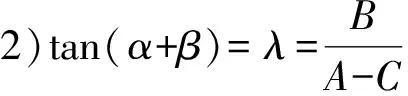
(其中Ф1=2Ax0+By0+D，Ф2=Bx0+2Cy0+E)．

证明 设点Q的坐标为(xQ,yQ)，点R的坐标为(xR,yR)，作平移：x′=x-x0，y′=y-y0，代入Ф(x，y)=0得

设QR的方程为lx′+my′=1，代入式(1)得到关于y′和x′的齐二次方程

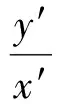
(A+Φ1l)=0.

(2)

又tan(α+β)=λ，于是

即l(Φ2-λΦ1)+m(Φ1+λΦ2)=λ(A-C)-B.

(3)

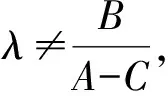
于是直线QR:lx′+my′=1在坐标系x′O′y′中过定点

即动直线QR过定点

l(Φ2-λΦ1)+m(Φ1+λΦ2)=0,

即

亦即

当定理中的常态二次曲线Ф为抛物线y2=2px时，tan(α+β)=λ(其中λ≠0)为定值的充要条件是动直线QR过定点

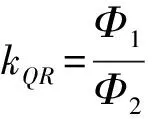
当定理1中的常态二次曲线Ф为抛物线y2=2px时，kPQ+kPR=0的充要条件是

上述性质，不仅形式优美，而且能帮助我们迅速破解某些试题，限于篇辐,仅举3例．

图2

例1 如图2所示，过抛物线y2=2px(其中p>0)上一定点P(x0,y0)(其中y0>0)，作2条直线分别交抛物线于A(x1,y1)，B(x2,y2)．

1)略；

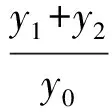
(2004年北京市数学高考理科试题第17题)

2)证明 由题意kPA+kPB=0，根据推论2，得

故

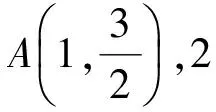
1)求椭圆C的方程；

2)E,F是椭圆C上的2个动点，如果直线AE的斜率与AF的斜率互为相反数，证明：直线EF的斜率为定值，并求出这个定值．

(2009年辽宁省数学高考文科试题第22题)

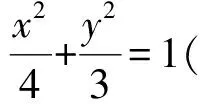
2)证明 由题设可知kAE+kAF=0，根据推论2知kAE+kAF=0的充要条件是

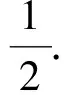
图3

(2011年全国高中数学联赛一试第11题)

2016-03-17；

2016-04-26.

石向阳(1972-)，男，湖南邵阳人，中学高级教师，研究方向：数学教育.

O123.1

A

1003-6407(2016)06-42-04