化曲为直：直观与严谨性的完美结合——谈利用曲线的切线判定零点的存在性

●唐 庚 李 敏 (中国人民大学附属中学分校 北京海淀 100086)



化曲为直：直观与严谨性的完美结合
——谈利用曲线的切线判定零点的存在性

●唐 庚 李 敏 (中国人民大学附属中学分校 北京海淀 100086)

文章利用曲线的切线界定其发展趋势，在探究复杂函数零点过程中，利用切线的零点的可求性，将对应的函数值进行放缩，从而找到变号零点的所在区间，改进了以往仅凭函数图像发展趋势直观说明的解决方式.

化曲为直;零点;切线;探究

零点是高中数学中函数内容的一个重要概念,也是近年高考的热点之一.可是有时我们明知它的存在，却不知它到底在哪里.下面举例说明.

例1 已知函数f(x)=ax2-ex(其中a∈R),f′(x)是其导函数(其中e为自然对数的底数)，若f(x)有2个极值点x1,x2，求实数a的取值范围.

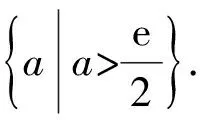
上述2种解法，都是在函数与方程之间相互转化，体现了数形结合的思想，训练了学生解决问题的能力.但细细品来，觉得整个过程直观性有余而严谨性不足.数学的根本任务在于优化学生的思维品质，发展思维水平和能力，上述解法给人草草收兵、戛然而止的感觉，似乎意犹未尽.

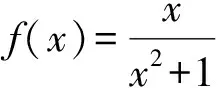
为了完整地解决这个问题，我们首先回顾一下函数零点的定义：一般地，如果函数y=f(x)在实数a处的值为0，即f(a)=0,则a叫做这个函数的零点.如果函数y=f(x)在一个区间[a,b]上的图像不间断，并且在它的2个端点处的函数值异号，即f(a)f(b)<0,则这个函数在这个区间上至少有一个零点，即存在一点x0∈(a,b),使得f(a)=0，并称这样的零点为变号零点,即零点存在定理.还有一类叫做不变号零点[1].

上述定义与定理，是我们判定零点是否存在的重要依据.如果是变号零点，我们有必要指出这个零点存在范围(区间).

我们先求曲线y=2ax-ex在x=ln4a(这是一个任意选定、便于计算的值，当然ln4a∈(ln2a,+∞))处的切线，易得切点为(ln4a,2aln4a-4a)，切线斜率为-2a，因此切线方程为

y=-2ax+4aln4a-4a.

下面先证明曲线y1=2ax-ex始终位于直线y2=-2ax+4aln4a-4a的下方.

构造函数

F(x)= 2ax-ex-(-2ax+4aln4a-4a)=

4ax-ex-(4aln4a-4a)，

则

F′(x)=4a-ex,

可知在(-∞,ln4a)上，F′(x)>0,F(x)单调递增,在(ln4a,+∞)上，F′(x)<0,F(x)单调递减,因此F(x)在x=ln4a处取得极大值.因为F(ln4a)=0,所以2ax-ex≤-2ax+4aln4a-4a在(-∞,+∞)上恒成立,即曲线y1=2ax-ex始终在直线y2=-2ax+4aln4a-4a下方,当x=2ln4a时(这也是在(ln2a,+∞)内一个任意选定、便于计算的值),y2|x=2ln4a=-2a·2ln4a+4aln4a-4a<0,从而g(2ln4a)<0.说明函数f′(x)=g(x)=2ax-ex在[ln2a,2ln4a]上存在x2使得g(x2)=0，故函数g(x)分别在区间(0,ln2a),(ln2a,2ln4a)内各有一个零点x1,x2.即f(x)有2个极值点x1,x2.

严格说来，函数变号零点若存在，都应该通过其在某个区间上端点值的异号来解决.很多情况下，这2个端点不易找到，于是有的解答只能依赖图像直观断定，有的更是借助x→+∞时的趋势，让人产生只可意会不可言说的感觉.数学的科学性与严谨性在此也打了折扣.我们采用化曲为直的方式可以部分解决这类问题.

再来看一个流传甚广的例子：

2015年北京市朝阳区高三一模考试中有如下问题(改编)：

命题组给出的标准答案如下：

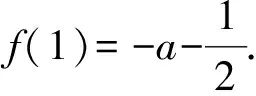
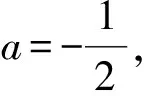
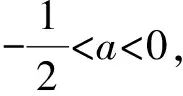
标准答案对第1)和第2)种情况的讨论是没有疑问的.但第3)种情况是从函数的发展趋势上判定其图像不是以x轴为渐近线，因此图像在极值点的左、右2侧都会穿过x轴，从而有2个零点.这么做，与其说是显然，不如说是无奈之举,缺少理性思维，没有深度，数学味随之降低.下面借助切线对零点的存在性予以证明.

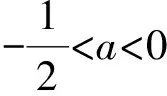
其中Δ=1+2a>0,因此上述方程有2个相异实根

在x=x1处，

g(x1)=-a(x1-1)>-alnx1=h(x1),

从而

f(x1)=g(x1)-h(x1)>0.

同理，在x=x2处

g(x2)=-a(x2-1)>-alnx2=h(x2),

从而

f(x2)=g(x2)-h(x2)>0.

调整后的解法，不再仅凭函数图像的趋势定性说明,而是将曲线转化为直线.这里的化曲为直，本质是放缩法，是不等量代换,它将不可比较的含有指、对数与多项式的混合函数，转化成了多项式函数，从而使计算成为了可能.这比凭运气去找到某个自变量使其函数值为正显然要有依据、有规律，也更容易为人所接受，体现了数学的严谨性.

以上2个问题都包含了转化与化归的思想.数学解题就是在不断转化，化归的基本目标是将生疏化为熟悉、将复杂化为简单、将抽象化为直观.但是选择合理的有效的转化途径很重要,这就需要我们善于发现知识间的联系并用于解决新问题，这也是数学创造性思维的重要特征.教师要有意识地选择一些具有挑战性的问题，为发展学生思维、培养创新意识提供舞台.

新课标指出：高中数学课程应注重提高学生的数学思维能力.数学的学习，在于培养人的理性精神、理性的思维方式[2]，如果仅作图形上的直观解释，势必会使学习流于肤浅，缺乏深刻性.爱因斯坦说过：“为什么数学比其他一切科学更受到特殊尊重，一个理由是它的命题是绝对可靠的和无可争辩的，而其他一切科学的命题在某种程度上都是可争辩的，并且经常处于会被新发现的事实推翻的危险之中.”我们教师任重而道远.

[1] 人民教育出版社中学数学室.普通高中课程标准实验教科书《数学(必修1)》(B版)[M].北京：人民教育出版社,2007.

[2] 中华人民共和国教育部.普通高中数学课程标准(2003版)[M].北京：人民教育出版社,2013.

2016-03-10；

2016-04-26.

唐 庚(1971-)，男，北京海淀人，中学高级教师，研究方向：数学教育.

O122

A

1003-6407(2016)06-34-03