圆锥曲线问题减少运算量的几点妙法

●吴灵喜 (兰溪市第三中学 浙江兰溪 321100)



圆锥曲线问题减少运算量的几点妙法

●吴灵喜 (兰溪市第三中学 浙江兰溪 321100)

圆锥曲线是数学高考的必考内容，综合运算能力是其要考查的能力之一.圆锥曲线问题思维量大，运算繁杂，很难得到完整解决.因此若能选择运用合理的运算方法，减少运算量，提高正确率,将事半功倍.

圆锥曲线;运算量;技巧;性质

圆锥曲线题以其思维量大、运算繁杂而使多数学生胆颤心惊．综观历年数学高考真题，固然有一些试题是考查学生的运算能力和坚韧不拔的意志(这是高考着重要考查的一个方面)，但不可否认，有些试题只要稍稍留意，平时积累一点运算技巧，便能减少运算量，节约解题时间，提高正确率[1]．

1 巧设点坐标

许多圆锥曲线问题都有涉及曲线上的动点和直线与它的交点问题，对点的坐标的处理将直接影响计算量．点的坐标有时设而不求，有时设而要求，有时迂回曲折，险中求胜．

1)求p的值；

x2-4px+4p=0.

设M1(x1,y1),M2(x2,y2),则

kM1F+kM2F=0,

即

从而

于是

即

p=4(此时满足Δ>0).

2)学生的常见思路是由点M2,A的坐标求直线AM2的方程，与抛物线方程联立，求出点M3的坐标.此过程太过于繁杂，结果只有放弃．说明这时强攻硬拼不行，得另寻思路．下面给出第2)小题的2种解法:

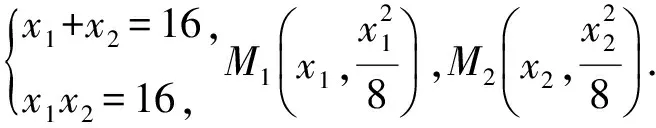
kM2M3=kAM2,

因此

即

整理得

x2x3-t(x2+x3)=-16.

(1)

同理由点B,M3,M1共线可得

式(2)的2边同乘以x2，得

x1x2x3-s(x1x2+x2x3)=-16x2,

即 16x3-s(16+x2x3)=-16x2.

(3)

由式(1)得x2x3=t(x2+x3)-16，

代入式(3)得

16x3-16s-ts(x2+x3)+16s=-16x2，

即

16(x2+x3)=st(x2+x3)，

从而

st=16,

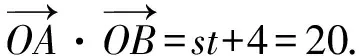
评注 此法技巧性强，没有一定的恒等变形能力及较强的预见性是不敢下笔的．

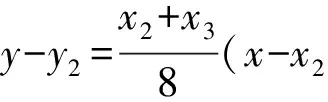
令y=2，得

同理可得

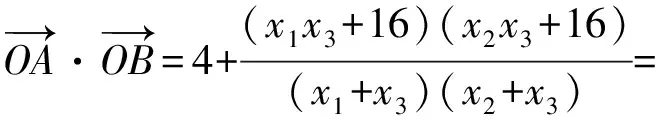
2 妙设直线方程

直线方程有5种表示形式，选择哪种形式对计算量有很大影响.

1)求C1的方程；

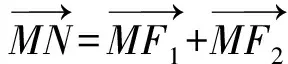
因此

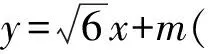
若用点斜式设直线l的方程为

代入椭圆方程得

9x2+16mx+8m2-4=0．

3 适当运用平面几何性质

尽管解析几何的精髓是用代数的方法研究平面曲线问题，但有时代数语言与几何语言互相切换，妙用平面几何性质，能达到计算最优化[2]．

1)求椭圆C的方程.

2)在椭圆C上，是否存在点M(m,n)，使得直线l:mx+ny=1与⊙O:x2+y2=1相交于不同的2个点A，B，且△AOB的面积最大？若存在，求出点M的坐标及对应的△AOB面积；若不存在，请说明理由．

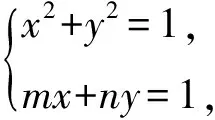
(m2+n2)x2-2mx+1-n2=0，

由韦达定理得

从而

整理可得

m2+n2=2.

又m2+3n2=3,得

方法2 假设存在满足条件的点M，则

从而

m2+3n2=4，

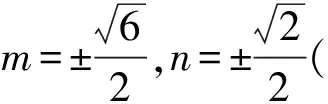
因此

m2+n2=2(下略)．

评注 方法3仅用了一点平面几何知识，就使运算量骤减，另外如何防止思维定势也是值得大家深思的．

4 用已知直线降次减少运算量

圆锥曲线问题离不开直线相交，利用直线方程能达到x,y相互切换，给复杂的代数式化简变形助一臂之力[3]．

例4 设抛物线C的顶点在原点，焦点F在x轴上，已知抛物线C上横坐标为3的点到C的准线的距离等于4．

1)求抛物线C的方程；

2)设点N(3，0)，过点F的直线交抛物线C于点A，B，求|NA|·|NB|的最小值．

分析 1)求得抛物线的方程为y2=4x.

y2-4ty-4=0，

由韦达定理得

y1+y2=4t,y1y2=-4,

从而

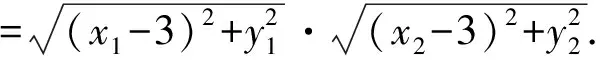
做到这里学生思维受阻了，出现次数较高的非对称式，韦达定理也很难用上．请看下面的迂回曲折的变换，最后如探囊取物：

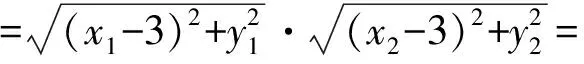
当且仅当t=0时，等号成立，因此|NA|·|NB|的最小值为8．

5 合理应用常用性质

若教师对例、习题中蕴含的性质,能让学生先自行证明，再结合历年高考真题强调其作用，则效果不言而喻．

( )

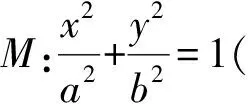
A．圆 B．椭圆 C．双曲线 D．抛物线

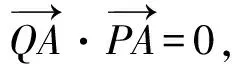
(-a-m,-n)· (-a-s,-t)=

(a+m)(a+s)+nt=0;

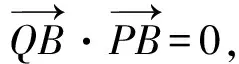
(a-m,-n)· (a-s,-t)=

(a-m)(a-s)+nt=0，

解得

(4)

又点P在椭圆M上，可令

由式(4)和式(5)得

从而

即点Q的轨迹是椭圆．

评注 此法设参较多，且要用到椭圆的参数方程，没有一定的实力是很难解决的．

由“椭圆第三定义”知点Q的运动轨迹是椭圆(人教A版《数学(选修2-1)》第41页例3的具体应用)．

有些题目不仅运算量大，而且有时毫无思路，运用性质，能够减少运算量，还能豁然开朗．

以上几点做法只能算是雕虫小技，难登大雅之堂，不过雕虫小技虽很少单打独斗，联合起来就能发挥大的威力，再结合分析解题思路的预见能力、敏捷的思维能力和过硬的计算能力，完美解决圆锥曲线题也不是不可能的事情．

[1] 赵春祥.优化圆锥曲线运算的10种方法与技巧[J].高中数理化,2015(7)：9-11.

[2] 范运灵,郑文祥.减少解析几何运算量的若干策略[J].数理化学习,2014(3):18-19.

[3] 曹兴旺.例谈圆锥曲线问题中解题方法的优化[J].中学生数学,2015(4):19-20.

2016-02-24；

2016-04-08.

吴灵喜(1969-)，男，浙江兰溪人，中学一级教师，研究方向：数学教育.

O123.1

A

1003-6407(2016)06-22-04