时间分层病例交叉研究的R软件实现*

张彩霞 刘志东 张斐斐 丁国永 姜宝法Δ

·计算机应用·

时间分层病例交叉研究的R软件实现*

张彩霞1，2刘志东1，2张斐斐1，2丁国永3姜宝法1，2Δ

时间分层病例交叉研究是病例交叉研究的一种，适用于多变量的时间序列资料，现已广泛应用于环境污染、气象因素、极端天气事件对人群健康影响的研究。经典的分析方法是条件 logistic回归，常采用SPSS中的COX回归模块以及SAS的proc phreg、proc logistic过程实现，最近一些新的分析方法如Poisson回归、条件Poisson回归也被逐渐应用到病例交叉研究中，但目前国内尚无此类方法如何用软件实现的相关文献报道。此外，病例交叉研究的资料整理比较复杂，虽已有彭晓武［1］等有关应用SAS整理双向对称病例交叉研究资料的方法介绍，但时间分层病例交叉资料的整理方法尚未见报道。因此，本文借助R软件通过实例分析来实现基于时间序列的时间分层病例交叉资料的整理及统计分析，包括利用“season”包中的casecross函数实现时间分层病例交叉资料的条件logistic回归分析，利用glm函数实现Poisson回归分析，利用“gnm”包中的gnm函数实现条件Poisson回归，最后利用山东省济南市2005年8～9月期间洪水对细菌性痢疾每日发病例数影响的时间分层病例交叉研究数据集进行验证。

时间分层病例交叉研究方法简介

病例交叉研究（case-crossover study）是由Maclure在1991年首次提出，它是一种用于研究短暂暴露对罕见急性病的瞬间影响的流行病学方法［2］。病例交叉研究可以看作病例对照研究的配对设计，它以病例自身作为对照不仅避免了选择对照所引起的偏倚，而且可以避免各病例之间一些不可控制的因素（如年龄、智力、遗传等）所引起的偏倚。当对照数据是暴露人时时，病例交叉研究也可以看作回顾性的队列研究，其分析可以按许多样本只含有一个个体的队列研究的荟萃分析来处理。病例交叉研究中交叉的思想来自于实验性交叉研究，后者实验对象经历两个处理阶段，而且各自作为自身对照以控制个体差异的影响；前者研究对象同时经历不同的时期即危险期和对照期，通过比较个体在不同时期的暴露情况得出疾病与暴露的关联［3］。时间分层病例交叉研究的基本原理是将时间进行分层，病例期和对照期处于同一年、同一个月和同一个星期几（the day of week），而且在同一时间层内，几个对照期是随机分布的，病例期并非固定在某一位置。例如，假设病例期发生在2014年12月12日（星期五），则2014年12月其他的星期五均被选为对照期（见图1）。

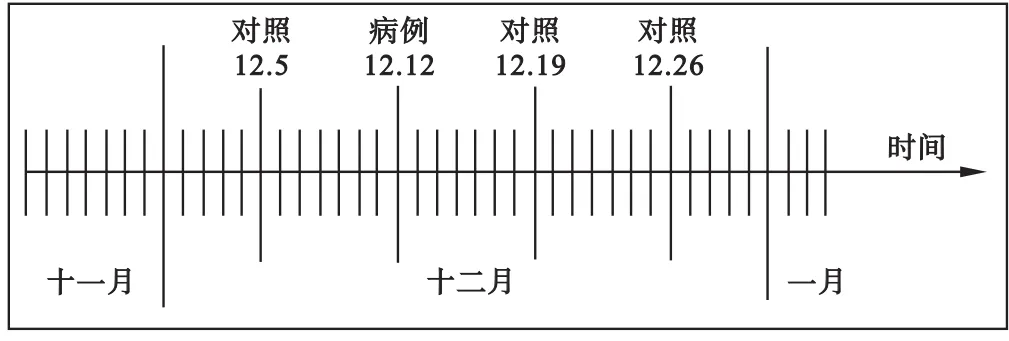
图1 时间分层病例交叉设计对照期选择示意图

时间分层病例交叉设计相当于按时间层匹配的病例对照研究，Janes［4］等通过统计模拟的方法发现，时间分层病例交叉研究可以同时控制季节性与星期几效应等混杂因素、消除时间趋势偏倚，并能得到参数的无偏估计（条件logistic回归）。而Poisson回归和条件Poisson回归通过设置哑变量（年、月、星期几）的方法，同样能达到按时间层匹配的目的。

实例与R软件分析

1.资料概述

现以伦敦的一个空气污染与人群死亡数据集为例演示时间分层病例交叉设计的软件操作［5］。数据集包含从2002年1月1日到2006年12月31日期间，伦敦市每天的臭氧浓度（ozone）、温度（temperature）、相对湿度（relative＿humidity）以及总死亡数（numdeaths）。所研究的暴露因素是臭氧浓度，健康结局是总死亡数，两个潜在的混杂因素是温度和相对湿度。数据集可以在 http://ije.oxfordjournals.org/content/suppl/2013/05/30/dyt092.DC1下载。

2.数据导入及变量预处理

library（foreign）＃加载 foreign包

data＜-read.dta（“londondataset.dta”）＃导入数据集

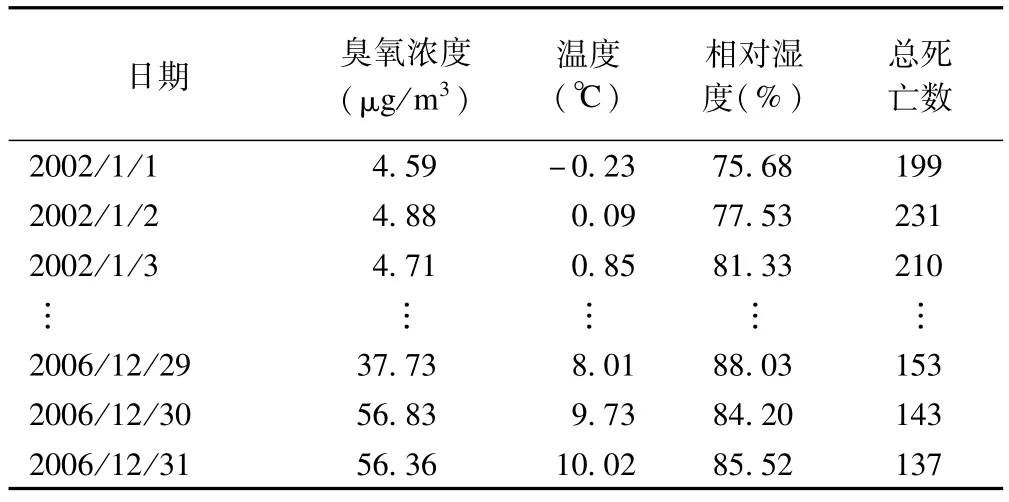
表1 伦敦空气污染与人群死亡数据集（部分）

data＄temp＜-data＄temperature＃重命名温度

data＄rh＜-data＄relative＿humidity＃重命名相对湿度

data＄dow＜-as.factor（weekdays（data＄date））＃添加星期元哑变量

data＄month＜-as.factor（months（data＄date））＃添加月份变量

data＄year＜-as.factor（format（data＄date，format＝“%Y”））＃添加年份变量

data＄stratum ＜-as.factor（data ＄year:data＄month:data＄dow）＃添加时间层变量

3.利用“season”包中的casecross函数实现条件logistic回归

library（season）＃加载 season包

model1＝casecross（numdeaths～ozone＋temp＋rh，matchdow＝TRUE，stratamonth＝TRUE，data＝data）

＃用 matchdow＝TRUE，stratamonth＝TRUE匹配同一年同一月同一个星期几

summary（model1）＃汇总结果

4.利用glm函数实现泊松回归

model2＜-glm（numdeaths～ozone＋temp＋rh＋factor（stratum），data＝data，family＝poisson）

summary（model2）

5.利用“gnm”包中的gnm函数实现条件Poisson回归

library（gnm）＃加载 gnm包

model3＜-gnm（numdeaths～ozone＋temp＋rh，data＝data，family＝poisson，eliminate＝factor（stratum））

summary（model3）

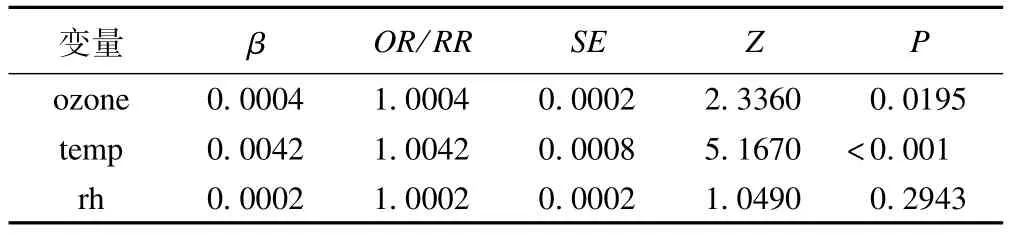
表2 R软件casecross、glm、gnm函数过程参数估计结果

上述三种方法的结果列于表2，可见条件logistic回归、Poisson回归和条件Poisson回归3种方法的结果是完全一致的，其中条件logistic回归得到的结果为比值比（odds ratio，OR），Poisson回归和条件 Poisson回归得到的是危险度比（risk ratio，RR）。

6.现应用以上R程序研究山东省济南市2005年8～9月期间洪水对细菌性痢疾每日发病例数的影响，暴露因素为洪水（flood，用二分类变量0、1表示，研究期间发生了两次洪水分别为8月1～2号和9月19～21号），健康结局是济南市细菌性痢疾每日发病例数（N），欲控制的两个潜在混杂因素为平均温度（AT）和平均相对湿度（ARH）。具体数据见表3。

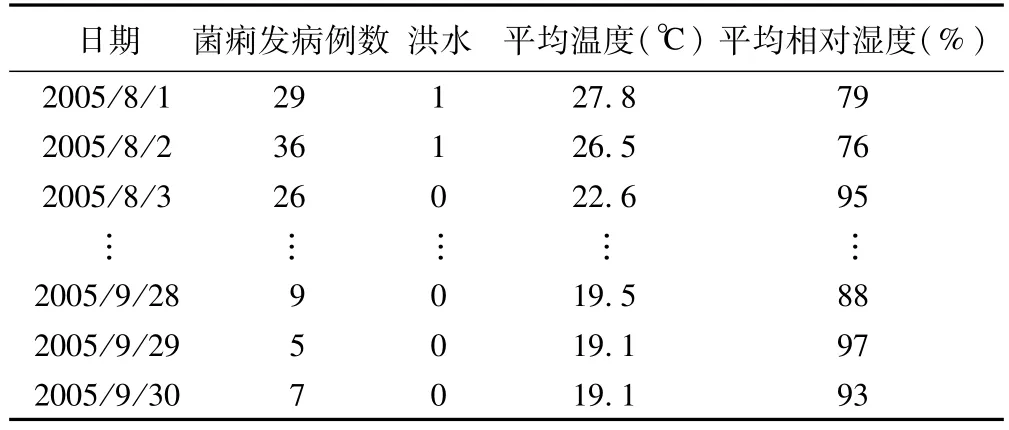
表3 济南市2005年8－9月洪水状况、气象因素与菌痢发病数数据集（部分）

将上文中介绍的条件logistic回归、Poisson回归和条件Poisson回归3种方法应用于研究山东省济南市2005年8～9月期间洪水对细菌性痢疾每日发病例数的影响，得到的结果是一致的（见表4）。

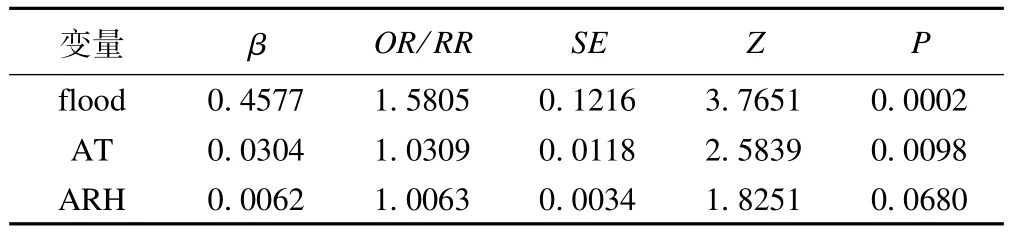
表4 洪水对细菌性痢疾发病数影响的参数估计结果

7.过离散、自相关、滞后等相关问题，以Poisson回归为例

（1）控制过离散:

model4＜-glm（numdeaths～ozone＋temp＋rh＋factor（stratum），data＝data，family＝quasipoisson）

summary（model4）

用quasipoisson代替poisson分布族控制过离散现象

（2）控制自相关:

library（tsModel）＃加载 tsModel包

reslag1 ＜-Lag（residuals（model4，type＝“deviance”），1）＃提取模型残差项

model5＜-glm（numdeaths～ozone＋temp＋rh＋reslag1，data＝data，family＝quasipoisson）＃通过加入残差项控制1阶自相关

summary（model5）

（3）单滞后模型:

library（Epi）＃加载 Epi包

library（tsModel）＃加载 tsModel包

tablag1＜-matrix（NA，7＋1，3，dimnames＝list（paste（“Lag”，0:7），c（“RR”，“ci.low”，“ci.hi”）））＃建立7行3列的表格

for（i in 0:7）｛numdeathslag＜-Lag（data＄numdeaths，-i）

model6＜-glm（numdeathslag～ozone＋temp＋rh＋factor（stratum），data＝data，family＝quasipoisson）

tablag1［i＋1，］＜-ci.lin（model6，subset＝“ozone”，Exp＝T）［5:7］｝

tablag1＃建立滞后变量，并依次估计不同滞后的参数，结果放在tablag1表格

（4）分布滞后模型:

library（dlnm）＃加载 dlnm包

cbozone＜-crossbasis（data＄ozone，lag＝c（0，7），argvar＝list（type＝“lin”，cen＝0），arglag＝list（type＝“integer”））＃建立臭氧与滞后的交叉基

model7＜-glm（numdeaths～cbozone＋temp＋rh＋factor（stratum），data＝data，family＝quasipoisson）

pred＜-crosspred（cbozone，model7，at＝10）

＃cen＝0指臭氧浓度参照水平为0 ug/m3，at＝10指相对于0μg/m3，臭氧浓度为10ug/m3的效应

tablag2 ＜-with（pred，t（rbind（matRRfit，matRRlow，matRRhigh）））＃提取 RR值及可信区间

colnames（tablag2） ＜-c（“RR”，“ci.low”，“ci.hi”）

tablag2

pred＄allRRfit；pred＄allRRlow；pred＄allRRhigh＃不同滞后的累积效应

讨论与小结

本文应用R软件进行时间分层病例交叉资料的统计分析，简化了时间序列资料繁琐的整理，增加了统计方法选择的灵活性。R软件开源、免费，近年来在数据探索、统计分析、作图等领域应用广泛，其帮助功能十分强大，本文中出现的所有命令、参数都可以通过帮助系统找到其详细解释。针对3种不同的统计方法进行R软件实例分析后，结果显示三种方法参数估计的结果是一致的。利用我们的洪水发生情况与细菌性痢疾发病数数据集进行验证也得到了相同的结果。国外多项研究亦表明，时间分层病例交叉设计的条件logistic回归与泊松回归分析是等价的［6－8］。条件logistic回归是病例交叉设计最常用的统计分析方法，但其并不能控制时间序列数据的自相关、过离散等问题，对此我们可以利用Poisson回归来控制这些问题，但Poisson回归也存在估计参数较多的缺点。条件Poisson回归是Poisson回归的进一步发展，其显著优点是减少了需要估计的参数，缩短了软件运算的时间，同时又不影响参数估计的准确性［9］。本文同时针对相关研究中的自相关、过离散、滞后等问题进行了R软件操作，提供了一个简便灵活的R程序。读者进行时间分层病例交叉设计的统计分析时，建议结合数据特点选择合适的方法灵活分析。

［1］彭晓武，余松林，相红，等.用SAS程序整理病例交叉设计资料.中国卫生统计，2012，29（1）:135-138.

［2］Maclure M.The case-crossover design:amethod for studying transient effects on the risk of acute events.Am J Epidemiol，1991，133（2）:144-53.

［3］胡以松.病例交叉研究.疾病控制杂志，2001，5（4）:341-343.

［4］Janes H，Sheppard L，Lum ley T.Case-crossover analyses of air pollution exposure data:referent selection strategies and their implications for bias.Epidemiology，2005，16（6）:717-726.

［5］Bhaskaran K，Gasparrini A，Hajat S，et al.Time series regression studies in environmental epidemiology.International journal of epidemiology，2013，42（4）:1187-1195.

［6］Levy D，Lum ley T，Sheppard L，etal.Referent selection in case-crossover analyses of acute health effects of air pollution.Epidemiology，2001，12（2）:186-192.

［7］Lu Y，Zeger SL.On the equivalence of case-crossover and time series methods in environmental epidemiology.Biostatistics，2007，8（2）:337-344.

［8］NavidiW.Poisson Regression and the Case-Crossover Design:Similarities and Differences.Communications in Statistics（Theory and Methods），2008，37（2）:213-220.

［9］Armstrong BG，Gasparrini A，Tobias A.Conditional Poisson models:a flexible alternative to conditional logistic case cross-over analysis.BMC Medical Research Methodology，2014，14（1）:122.

国家重大科学研究计划（973计划）项目（2012CB955502）

1.山东大学公共卫生学院流行病学系（250012）

2.山东大学气候变化与健康研究中心

3.泰山医学院公共卫生学院

△通信作者:姜宝法，E-mail:bjiang@sdu.edu.cn

（责任编辑:邓 妍）