运用有效策略促进概念的理解与巩固
2016-12-25孙保华
孙保华
教学是循序渐进的过程,学生对概念的掌握不是一次就能完成的,要由具体到抽象,再由抽象到具体多次往复。所以当学生初步建立新概念后还需要运用多种策略,促进概念在学生认知结构中的保持,并通过不断运用概念,加深对概念的理解,使学生建立的概念得以巩固。
一、重点字词理解策略
将体现概念本质属性、起决定作用的关键字、词、句,进行全面深刻的剖析、理解,从而达到概念清、方向明、判断准的效果。例如对“商不变规律”的解析如下:
1.用“___”标出重点字词:“除法、同时、相同的数、(0除外)”。
2.对重点字词的剖析、理解:(1)除法是前提。(2)同时:都要,一齐的意思。(3)相同的数:同一个数。(4)0除外:0不能作除数。
学生只有对这些关键词语(或词组)的真实含义都弄清楚了,才会对商不变规律有深刻的理解。
二、分解概念属性策略
就是当接触一个概念时,根据叙述的定义将概念分成几部分。再对每一部分进行深入细致地分析,弄清原理,抓住实质。最后把这几个部分进行综合,形成一个整体,这就包含了这个概念的全部内容。例如对正比例的意义进行分解如下:
1.确认概念名称——正比例。
2.分解概念要点:(1)有两种量;(2)它们是相关联的;(3)两种量要变化;(4)两种量相对应的两个数比值(商)不变。
3.分析理解每个要点:(1)有两种变量;(2)一种量变化引起另一种量变化;(3)变化时,两种量同时扩大(或缩小)相同的倍数;(4)这两种量中任意两个相对应数的比值(商)不变,即两种量相除有商不变的规律。
4.弄清联系,明确概念意义:两种量具备了以上3个条件(缺一不可)时,这两种量就叫做正比例的量,它们的关系叫做正比例关系。
三、易混概念对比策略
随着学习的深入,学生掌握的概念不断增多,有些概念的文字表述相同,有些概念内涵相近,使得学生容易产生混淆,如质数与分解质因数,体积与容积等。因此要注意组织学生运用对比的方法,弄清易混概念的区别和联系,以促使概念的精确分化。例如将求比值和化简比进行对比如下:
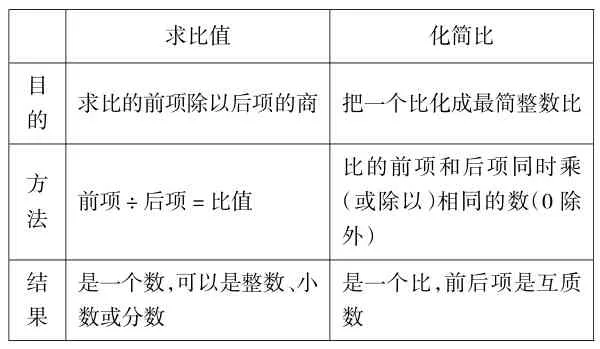
求比值________________________________________________化简比目的__求比的前项除以后项的商 把一个比化成最简整数比方法 前项÷后项=比值比的前项和后项同时乘(或除以)相同的数(0除外)结果__是一个数,可以是整数、小数或分数_______________是一个比,前后项是互质数____________________
四、运用变式辨析策略
教学中要充分运用肯定事例来强化学生对概念内涵的理解,同时要及时运用否定事例来促进学生对概念的辨析,进一步促进学生对概念本质属性的深刻理解。
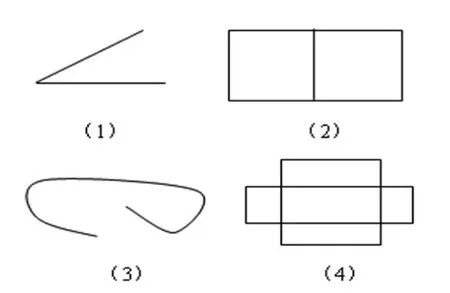
例如,在教学《认识周长》一课时,当学生通过肯定事例建立了周长的概念,但没有深入去剖析周长的本质属性,教师适时抛出下面的四个图形,让学生分别指出这些图形的周长。学生可能出现两种情况:一种是束手无策,不知道从何下手;一种是把所有的线都指一遍。此时,教师就问:“为什么你找不到图1和图3的周长呢?图2和图4的周长到底指哪部分?”通过学生的讨论、分析、辩论,学生能够明确图1和图3两个图形不是封闭图形,所以没有周长;而图2和图4的周长应该指的是这两个图形外面一圈线段的总长,与图形内部的线段没有关系。这里通过正、反两种方式进行对比、变式教学,学生对周长概念的理解由模糊到清晰,对周长的认识由感性认识上升到理性认识,明确周长这一概念的本质就是封闭图形一周的长度。
五、概念结构图解策略
所谓概念结构图解策略就是用一个结构图把相关联而又分散的知识系统化、条理化,从而形成知识网络的一种学习策略。形象地说就是根据知识之间整体与部分之间的关系、知识之间的内在规律与联系,搭设知识“骨架”,从而掌握“知识的全貌”。同时,系统化、结构化的知识更有利于学生的理解和保持,因此当学生学习了一定数量的概念后,教师就要帮助学生形成正确的概念系统。为此,教学中常用如下方法:
1.用分类的方法表示概念外延间的关系。通过分类可以揭示概念的外延,使知识条理化、系统化,防止概念的混淆。如三角形以角为标准,可分类为:

2.用增加内涵的方法表示概念内涵间的关系。随着概念内涵的增加,外延将缩小。据此,可以把概念整理成系统。如几种四边形内涵间的关系可用下图来表示。
3.用集合图表示概念外延间的关系。在揭示某些概念之间的关系时,可以用集合图。几种三角形外延间的关系可用下图来表示。
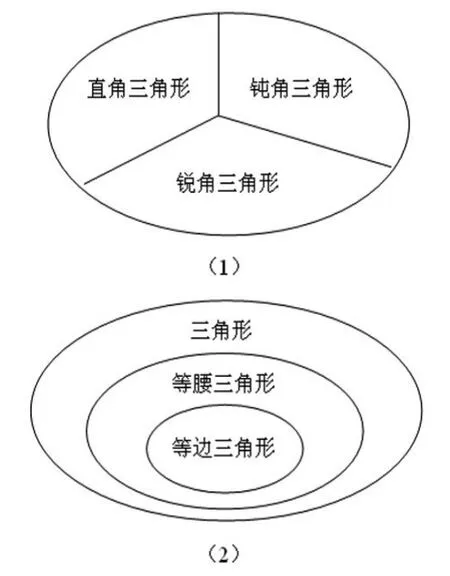
由图(1)可以直观地看到,在三角形中,直角三角形、锐角三角形和钝角三角形是并列的概念,它们的外延没有交叉。由图(2)可以直观地看到三角形、等腰三角形、等边三角形都是属种关系,后一概念的外延包含于前一概念的外延之中。
六、灵活应用概念策略
在概念教学中,既要引导学生由具体到抽象,形成概念,又要让学生由抽象到具体,运用概念。学生是否牢固地掌握了某个概念,不仅在于能否说出这个概念的名称和背诵概念的定义,而且还在于能否正确灵活地应用,通过应用可以加深理解,增强记忆,提高数学应用研究的意识。概念的应用可以从概念的内涵和外延两方面进行。
1.概念内涵的应用。如教学“真分数和假分数”可设计如下练习:
(1)什么叫真分数和假分数?
(2)判断。
分子比分母小的分数都是真分数。( )
分子比分母大的分数都是假分数。( )
假分数都比1大。( )
假分数就是分子比分母大的分数。( )
2.概念外延的应用。如教学“因数和倍数”可设计如下的练习:
(1)12的所有因数有( );50以内13的倍数有( )。
(2)在 9、10、8、11、13、15、21、30中,找出3的倍数和5的倍数,并把这些数分别填入下图的区域内。

(3)一个数是48的因数,这个数可能是( )。
一个数既是48的因数,又是8的倍数,这个数可能是()。
一个数既是48的因数,又是8的倍数,同时还是3的倍数,这个数是( )。
总之,在学生建立了正确的概念后,要运用各种有效策略,帮助学生澄清概念,从而深化概念的理解和巩固,使学生更清楚地认识知识的内在联系,促进学生认知结构的完善和发展,同时为概念的灵活运用做铺垫,培养学生的思维能力。
