卧式矩形截面螺旋通道内气液两相流截面含气率测量研究

周云龙孙 博

(东北电力大学能源与动力工程学院)

卧式矩形截面螺旋通道内气液两相流截面含气率测量研究

周云龙*孙 博

(东北电力大学能源与动力工程学院)

以空气和水为工质，对卧式矩形截面螺旋通道内气液两相流动特性进行了实验研究。根据以往截面含气率的计算方法，创新性地提出一种适合于卧式矩形截面螺旋通道内两相流动截面含气率的计算方法，并与漂移流模型进行比较，发现两种计算方法所得结果趋势相近，大部分符合较好，表明利用斜十字交叉法计算卧式矩形截面螺旋通道内气液两相流的截面含气率是可行的。并且对比Zuber-Findlay模型与Ishii模型发现，Ishii模型预测卧式矩形截面螺旋管通道内的截面含气率精度较高。

矩形截面螺旋通道 空气-水两相流 截面含气率 漂移流模型

螺旋管具有空间利用率大、可自由膨胀及重心低等优点，并且传热特性比直管的更佳[1]，是一种具有良好应用前景的高效换热管型。在研究两相流的过程中，两相流截面含气率是一个极其重要的参数，它的准确与否直接关系到设备运行的可靠性。因此，准确地测量和计算换热管段的含气率是设计换热管段的关键。近年来，不同形状和尺寸的螺旋通道内的流动机理越来越受到重视，但是，有关计算矩形截面螺旋通道内两相流的含气率的研究报道还是很有限的。

目前，对于圆形截面螺旋通道内气(汽)水两相流动特性已有广泛的研究[2～5]，但对于其他截面形状的螺旋通道，大部分还停留在数值研究阶段[6]，实验研究比较少。而仅有的对于矩形截面螺旋通道的实验研究也多是针对单相流体所进行的流场结构和流动特性的研究。对于螺旋管管内两相流的含气率的研究主要是在螺旋管立式放置的情况下进行的。实验结果与水平管的数据一致或稍大于水平管的数据。一些学者为了获得含气率的实验数据，基于漂移流模型提出了一些含气率的计算方法，认为流道尺寸对于漂移流模型研究很重要[7～10]。但是，非常规管径的实验数据较少，不足以对现有截面含气率计算模型进行评价分析。

本研究以空气-水为工质，实验测定了压差信号，针对卧式矩形截面螺旋通道内空气-水两相流动，提出一种新的计算卧式矩形截面螺旋通道内截面含气率的方法，并与漂移流模型进行对比，这对促进工程实际相关方面的发展具有重要的意义。

1 实验系统与装置

实验是在空气-水实验台上进行的，实验系统如图1所示。

通道由一个外壁带螺旋翅片的圆柱和一个外套管围成，为了实现可视化研究，材料采用有机玻璃，螺旋翅片由车刀车出，与外套管的配合公差小于1mm。外套管内径120mm、厚5mm，螺旋翅片高22mm、厚6mm、螺距110mm。所围成的矩形截面的长、宽分别为24mm和22mm。通道当量直径为23mm、曲率为0.47、挠率为0.36。本实验中，有效直管段的长度为550mm，即5倍螺距。

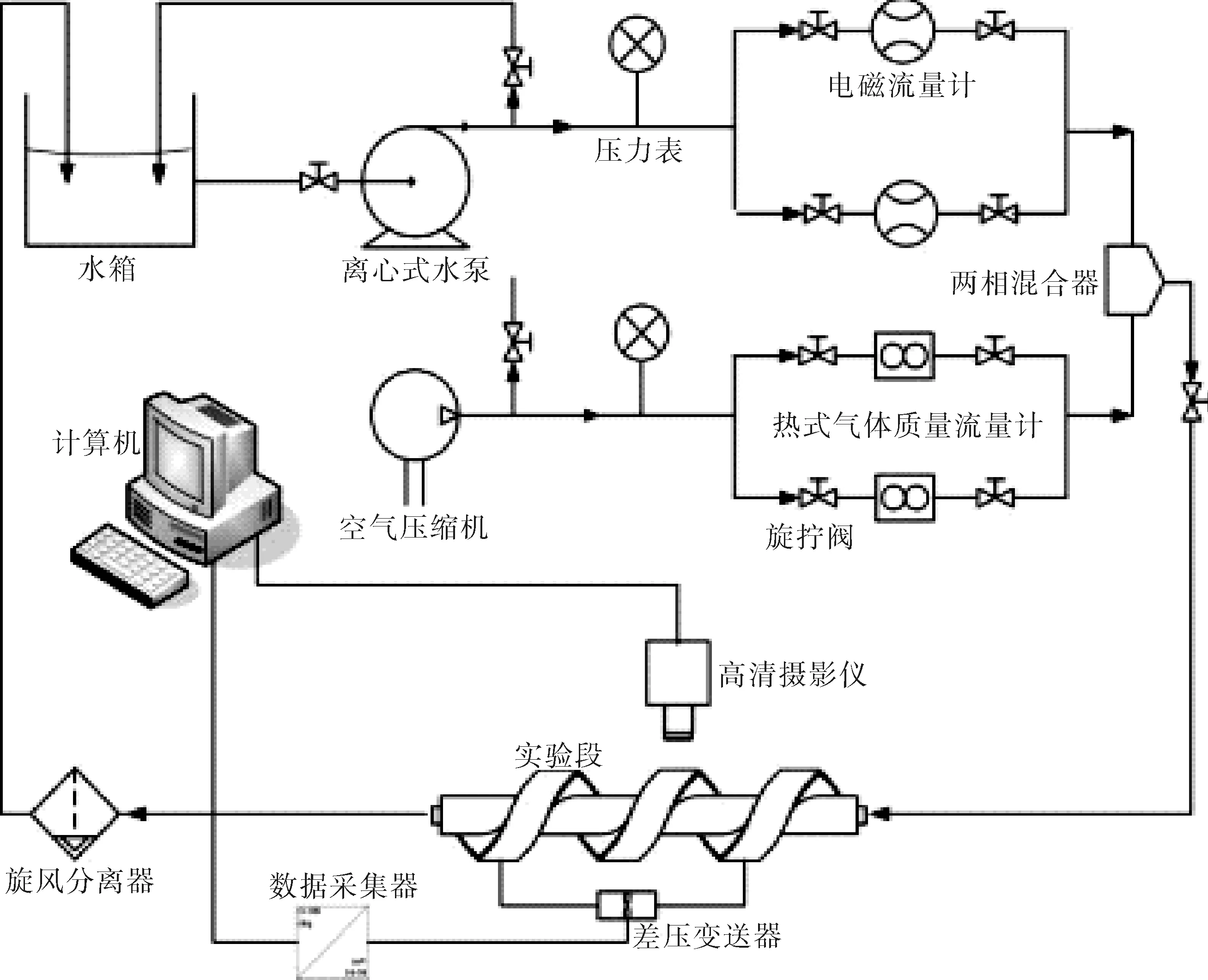
图1 实验台流程图

水和空气分别在离心式水泵和空气压缩机的动力推动下流经电磁流量计和热式气体质量流量计，经两相混合器充分混合后流入实验段，而后经旋风分离器分离，水流回水箱继续循环使用，空气排入大气中。空气压缩机额定工作压力为0.8MPa，实验过程在常温下进行，压力参数范围为0.1～0.3MPa。空气的折算速度范围为0.2～15.0m/s，水的折算速度范围为0.2～1.2m/s。本实验使用差压变送器采集机压差信号，并通过数据采集器输入计算机，用专门的软件处理。为保证测量信号的实时性，设定采样频率为512Hz，采集时间为10s，准确记录了压降与流量的信号变化。同时计算机还连接着高清摄影仪，记录较为典型的流型。本次实验选择实验段同一螺距上、下、左、右的4个取压点采集压差信号，且上下、左右分别为两组差压信号。实验采用的差压变送器在实验前使用电子手操器进行了量程校准。整个实验台的测量信息统一整理在表1中。

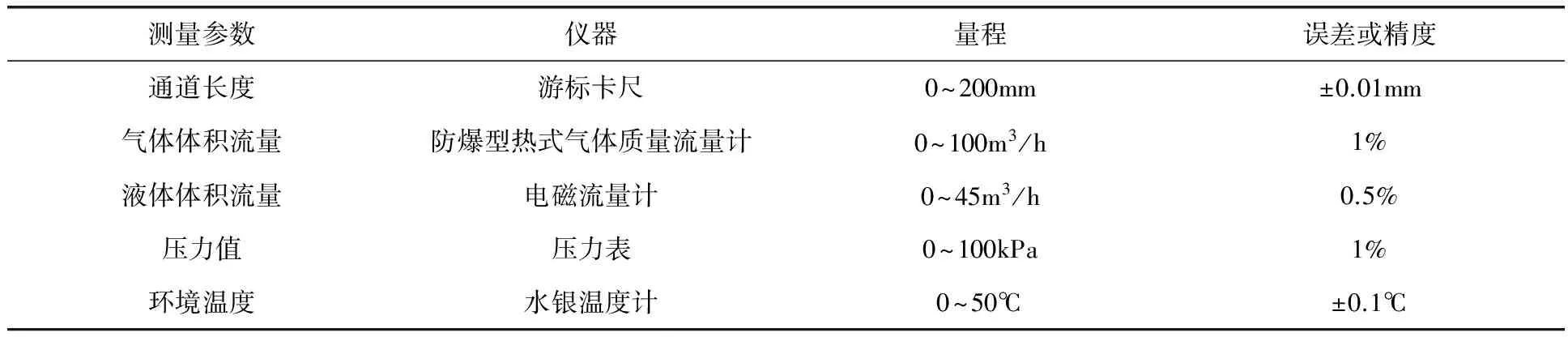
表1 测量参数和设备误差

实验系统安装完毕正式实验前，先对整个实验系统进行水洗，清除系统中的沉积物对实验系统的影响，然后对压力压差传感器进行仔细的标定、校核和检查。对于空气-水两相流实验，首先固定水的流量，改变气体流量使之从小到大间断变化，直至气体流量达到最大。在每一间断点工况下，观察并待流型稳定后进行记录和数据采集。完成一个循环后，然后再增大水的流量，重复调节气的流量。实验完毕后，应先关闭供水回路，再关闭供气回路。

2 截面含气率的测量

2.1截面含气率的测量方法

测量截面含气率的方法有很多，目前有一种采用水平管与垂直管组合的测量方法，该方法的核心思想是垂直管的摩擦阻力用水平段的摩擦阻力代替。根据总压降求出垂直管内的重力压降，进而从重力压降导出管内的平均截面含气率。

实验段总的压力降Δp可表示为重力压降、摩擦阻力降和加速压降之和。在泡状流和弹状流流动区域，由于加速压降通常远小于总的压降，因此可以忽略不计。垂直上升管内总的压降Δpv为重力压降与摩擦阻力降的和，而水平管内重力压降为零，因此水平管总压降Δph为摩擦阻力降。

垂直管内的重力压降ΔpUg为垂直管总压降减去水平管总压降：

ΔpUg=Δpv-Δph

(1)

其中：

ΔpUg=ρLgh

(2)

ρL=ρw(1-ag)+ρgag

(3)

式中ρg——空气的密度，kg/m3；

ρL——混合物的密度，kg/m3；

ρw——水的密度，kg/m3。

由此得出垂直管内平均截面含气率ag为：

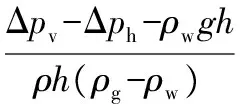
(4)

2.2矩形截面螺旋通道内气液两相流截面含气率的计算

本次实验借助水平管与垂直管组合的测量方法，创新性地提出斜十字交叉法计算矩形截面螺旋通道内的气液两相流截面含气率。

实验段如图2所示，设置了A、B、C、D4个取压点，A点设置在实验段底部，C点设置在顶部，B点设置在实验段中部A、C点之间，D点设置在C点之后与B点处于同一水平线上，两相流体先后流经A、B、C、D4点。压力测量装置分别测量AC段和BD段的压降。

图2 矩形截面螺旋通道实验段

在AC段内，也就是流体上升段，实验段总的压降Δp可表示为重力压降ΔpUg、摩擦阻力降ΔpUf与加速压降ΔpUa之和。同样的，在非湍流流动区域内加速压降一般远小于总的压降，可以忽略不计，因此在AC段内总压降可以表示为：

Δp=ΔpUg+ΔpUf

(5)

由于B、D两点处于同一水平线上，所以BD段的重力压降为0，根据上面的论述，AC段内的摩擦阻力降ΔpUf被水平段BD内的摩擦阻力降ΔpHf代替，因此AC段内的总压降可以表示为：

Δp=ΔpUg+ΔpHf

(6)

式(6)中的Δp和ΔpHf可通过实验测得，因此就可以求出AC段内的重力压降：

ΔpUg=Δp-ΔpHf

(7)

联立式(2)、(3)、(7)便得出AC段内平均截面含气率：

(8)

2.3实验值与漂移流模型的计算式对比

截面含气率的计算模型较多，主要归结为三大类模型，即滑速比模型、k-β模型和漂移流模型，其中漂移流模型应用最为普遍。目前，漂移流模型的计算式较多[10，11]，不同计算式之间的差别仅为由实验确定的分布参数C0和漂移速度表达式的不同。漂移流模型认为必须同时考虑气液两相之间的滑移、流速和空泡份额在流通截面上的不均匀分布，它在泡状流、弹状流等流型中的计算精度较高。Zhao T S和Bi Q C在研究气液两相流动截面含气率时，验证了漂移流模型计算截面含气率是可信的[12]。

利用漂移流模型计算空泡份额α的基本公式为：

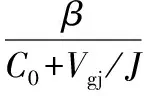
(9)

其中分布参数C0与截面上的速度和空泡率径向分布有关。

Zuber-Findlay模型中气相加权平均漂移速度Vgj的关系式是在常规通道中得到的，分布系数C0和气相加权平均漂移速度Vgj的计算式为：

C0=1.2

(10)

Ishii模型对分布系数C0和气相加权平均漂移速度Vgj的计算式为：

(11)

3 实验含气率计算结果与漂移模型计算结果的比较

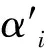
(12)

本实验运用斜十字交叉法测量、计算了矩形截面螺旋通道内气液两相流的截面含气率，并与漂移流模型计算结果进行了比较。

图3是根据斜十字交叉法计算出的含气率与漂移流模型的两种不同的计算式的含气率对比结果示意图，从图中可以清楚地发现两种计算方法所得结果在液体流量1.49～3.16kg/(m2·s)的范围内，实验值与漂移流模型的计算值大部分符合较好，误差几乎都在±20%以内。因此，可以初步得出结论：利用斜十字交叉法计算矩形截面螺旋通道内空气-水气液两相流的截面含气率是可行的。但是，Zuber-Findlay模型的平均绝对误差比Ishii模型的大，因此，Zuber-Findlay模型相比Ishii模型来说精度较低，所以可以使用Ishii模型来预测螺旋管内的截面含气率。

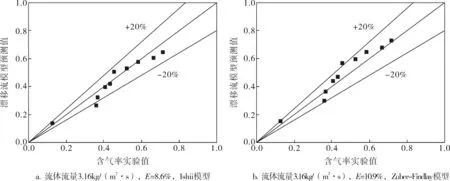
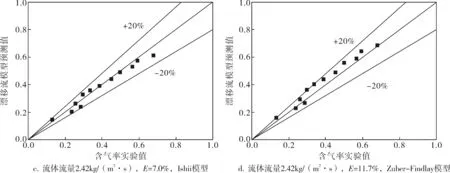
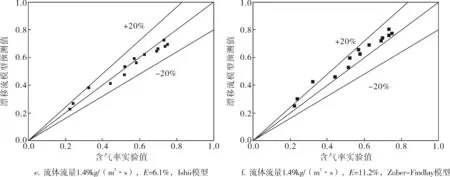
图3 斜十字交叉法与漂移流模型计算含气率的对比结果

4 结束语

本实验是借助水平管与垂直管组合的测量方法，创新性地提出斜十字交叉法来计算卧式矩形截面螺旋通道内气液两相流的截面含气率。利用斜十字交叉法对卧式矩形截面螺旋通道内气液两相流的截面含气率进行计算后的结果与漂移流模型预测值进行了比较，发现两种计算方法所得结果趋势相近，大部分符合较好，因此表明利用斜十字交叉法计算矩形截面螺旋通道内气液两相流的截面含气率是可行的。并且对比Zuber-Findlay模型与Ishii模型发现，Ishii模型来预测螺旋管内的截面含气率精度较高。但是本实验只是进行了空气-水气液两相的实验，因此并不能表示该方法也适用于其他工质。

[1] 陈学俊.两相流与传热-原理及应用[M].北京：原子能出版社，1991：18～20.

[2] Biswas A B，Das S K.Frictional Pressure Drop of Air Non-Newtonian Liquid Flow through Helical Coils in Horizontal Orientation[J].The Canadian Journal of Chemical Engineering，2007，85(2)：129～136.

[3] Biswas A B，Das S K.Two-phase Frictional Pressure Drop of Gasnon-Newtonian Liquid Flow through Helical Coils in Vertical Orientation[J].Chemical Engineering and Processing：Process Intensification，2008，47(5)：816～826.

[4] Santini L，Cioncolini A， Lombardi C，et al.Two-phase Pressure Drops in a Helically Coiled Steam Generator[J].International Journal of Heat and Mass Transfer，2008，51(19/20)：4926～4939.

[5] Murai Y，Yoshikawa S，Toda S，et al.Two-phase Pressure Drops in a Structure of Air-Water Two-phase Flow in Helically Coiled Tubes[J].Nuclear Engineering and Design，2006，236(1)：94～106.

[6] Xia G D，Liu X F，Zhai Y L，et al.Single-phase and Two-phase Flows through Helical Rectangular Channels in Single Screw Expander Prototype[J].Journal of Hydrodynamics，2014，26(1)：114～121.

[7] Hills J H.The Operation of a Bubble Column at High Throughputs：I.Gas Holdup Measurements[J]. The Chemical Engineering Journal，1976，12(2)： 89～99.

[8] Isao K，Mamoru I. Drift Flux Model for Large Diameter Pipe and New Correlation for Pool Void Fraction[J]. International Journal of Heat and Mass Transfer，1987，30(9)：1927～1939.

[9] Kawanishi K，Hirao Y，Tsuge A.An Experimental Study on Drift Flux Parameters for Two-phase Flow in Vertical Round Tubes[J].Nuclear Engineering and Design，1990，120(2)：447～458.

[10] Hibiki T，Ishii M.One-dimensional Driftflux Model for Two-phase Flow in a Large Diameter Pipe[J].International Journal of Heat and Mass Transfer，2003，46(10)：1773～1790.

[11] Zuber N， Findlay J A.Average Volumetric Concentration in Two-phase Flow Systems[J].Journal of Heat Transfer，1965，87(4)：453～468.

[12] Zhao T S，Bi Q C.Pressure Drop Characteristics of Gas-Liquid Two-phase Flow in Vertical Miniature Triangular Channels[J].Heat Mass Transfer，2001，44(13)：2523～2534.

ExperimentalResearchofMeasuringVoidFractionofGas-LiquidFlowwithinSpiralChannelwithHorizontalRectangularSection

ZHOU Yun-long, SUN Bo

(SchoolofEnergyandPowerEngineering,NortheastDianliUniversity,Jilin132012,China)

*周云龙，男，1960年2月生，教授。吉林省吉林市，132012。

TQ022.4

A

0254-6094(2016)05-0580-06

2015-11-04)

(Continued on Page 588)