基于高三数学试卷讲评课的教法探究与反思—以一道高考模拟解析几何题的教学为例

江苏省句容市第三中学(212400) 胡容锁

基于高三数学试卷讲评课的教法探究与反思—以一道高考模拟解析几何题的教学为例

江苏省句容市第三中学(212400) 胡容锁

高三频繁的模考统考,试卷讲评课将是高三阶段一个重要的课型,如何上好讲评课显得尤为必要.本文结合对2015年3月18日苏锡常镇四市情况调查测试第18题的一次讲评课的实录,与同行交流如何上好高三数学试卷讲评课的问题.

一、试题分析

1.1 试题呈现

图1

(2)求证:AP⊥OM;

解法一(2)设直线BM的斜率为k,则直线BM的方程为y=k(x−2),设P(x1,y1),将y=k(x−2)与椭圆C的方程联立化简得:

1.2 阅卷情况反馈

本题重点考察学生运算能力,设制第一问较简单,第二问较难,第三问承接第二问;体现了“让学生想得少,算得多”的命题理念.阅卷按照4-9-3规则给分.大部分学生解题表现不错,总体反映出学生基础知识、基本技能、基本方法掌握的较好.

主要问题有:

1.学生书写不规范、答题马虎、卷面整洁度差.

3.思路狭窄、解法单一.处理解析几何问题,使用点斜式和两点式直线方程是常用的两种途径.绝大多数学生选用设斜率的方法求解,显然运算量陡增,如果尝试利用设而不求的思想,设点M的坐标求解本题效率大大提高,运算过程更加优化.

4.算法不优、逻辑不严.本题可以设斜率,也可以设坐标,不同的设法,会增加及减少运算难度.再如没有证明而直接使用.

5.定位不准,应试技巧和抢分意识不强.针对0分卷的同学第1问还是可以得分的,也有些学生能力达不到还在第二小问部分苦思冥想,浪费时间;再则有同学最后答案为含有未知参数的代数式,本题是解析几何的定点定值问题,应消去或约去参量即得定值.

二、相关数据分析

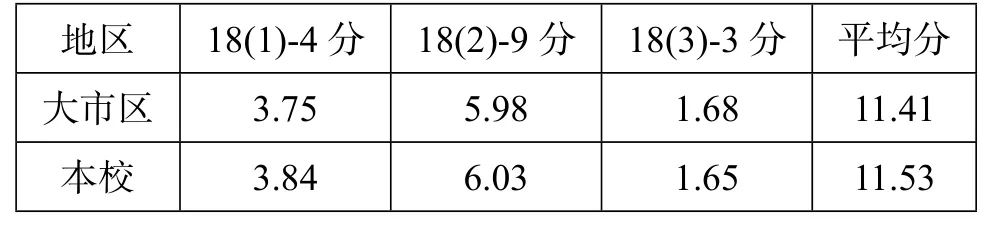
表1 18题三小问分值情况表

表2 18题技术指标分析情况表

由表1可知,本题平均分达到11.53分,主要在第二问上失分较多,我校不满9分的人数为325,说明学生在运算能力和解题技巧策略上亟待进一步强化.

从技术指标来看,区分度是衡量题目质量的一个重要标准,该题设计得较好、区分度高,难度属于中等难度的题目;不过还存在少量的零分卷,总体本题得满分的学生所占比重较大.

表3 考生18(2)解题策略情况对比表(随机选取200份样本)

解析几何中设斜率和设点坐标是常规的两种解题策略,显然本题学生选择策略一、策略二的比重最大,运用斜率解题的学生明显多于选用设点坐标的学生.失分多的原因在于方法策略上,平时“设而不求”方法不能灵活运用,导致本题运算量增大,影响得分.

三、课堂评讲实录

在充分了解学生答题数据情况下,针对本题笔者适时进行了如下过程的教学:投影学生的两种解题过程(即解法一和解法三),学生自行对比方法优劣.

师:对比上述两种方法,你认为选择哪种解题策略更优化?

生:(全体)解法三……

师:请你总结一下处理解几问题之前的注意事项.

生:方法策略的选择上应先前预估和判断,有利于提高解题效率.

简评学生对解题步骤方法进行归纳对比,让学生从整体上把握本题,从而避免解法单一,讲解不深入不透彻的问题.

师:我有个疑惑,看看大家是否可以帮我解决下.

问题1该题如果推广到一般情况下,是否同样可以得到AP⊥OM即(kAP·kOM=−1)?

师:请你解释一下我们验证出的结论?

生:当且仅当a2:b2=2:1时,才有kAP·kOM=−1.所以AP⊥OM是偶然的,不是必然,不论椭圆标准方程如何变化,kAP·kOM=−均为定值,不一定是−1.

简评渗透特殊与一般思想,提升学生研究数学素养.学生板演着重强调书写规范,实施有效教学示范,强化运算能力的过程教学.

问题2 kAP·kOM=与我们之前所学的椭圆定值问题中什么结论存在联系?

师:很好.大家仔细观察kOM与kPB表达式,能发现有什么内在联系?请尝试证明！

生:AB=2OB,则2tan∠MBx=tan∠MOB,即 2kBP=kOM,所以kOM·kAP=2kBP·kAP=−

师:此处应该有掌声.

简评联系学生的最近发展区,激发已有的知识,促进知识的迁移和转化;拓宽了知识面,进一步延展学生的解题视野,本题可以用这个结论快速的完成.顺理成章牵引出本题另一种更好的解题方法:解法五(如上).

问题3退化本题条件,曲线变成圆的方程x2+y2=r2,则kAP·kOM是否为定值?

生:kAP·kOM−2(证明略).

师:请同学们将该结论比较联系下问题2.有什么发现?

生:原来kAP·kOM=−2是在当a=b条件下kAP·kOM=−特殊情况而已.

生:(学生笔算,教师投影演示)kAP·kOM=(证明略)

简评学生活动踊跃,知识能力发生了迁移联系;激发了探索的欲望、渗透了类比思想.

图2

四、几点教学思考

1.重视数学书写解答规范性,提升学生运算能力不足

考生运用数学符号正确简洁地表达自己的意图的能力,是数学高考考查的能力之一,良好的书写习惯也是应试技巧的重要组成部分;增强学生书写规范性意识,减少隐形分数的丢失.

运算能力是数学高考考查的核心能力！高考必定有一道题专门直接考查数学运算能力,已成为解析几何瓶颈,教师可以引导学生黑板板演来强化书写规范,展示演算步骤时注重算法算理指导来简化运算过程,利用设而不求的方法、转化相关条件、注意整体代换等运算技能,从能力角度提高对运算的认识,反思运算失误的经验教训,不断提高运算水平.

2.改变满堂灌型“高效低能式”的教学

数学教学不能简单认为多做多讲,忽视学生参与,影响学生的后续能力发展.学生“上课热热闹闹,下课空空落落”的现象,原因在于整个课堂中教师几乎包办了学生思考过程,“替”验学生的心路历程;剥夺了学生独立思考,自主探索的需求.第18题大部分学生就是惯性思维而设斜率解题.课堂以问题式模式为驱动,引领学生不断思考、深入探究,不失时机地“抛砖引玉”启发引导,围绕问题解决展开,达到激发学生数学问题的求知欲,培养学生探究思考的好习惯.

3.转变教师重视“教”,忽视“研”现状

重视评讲试卷有内涵有代表性的题,通过变式训练拓展延伸解决相关一系列问题,不能就题讲题,要充分利用教材、模拟卷等一切教学资源,发现问题,挖掘问题共性特征,提炼出来进行有效地整理、归类;组织形成针对相关题型微专题研究,展开“从特殊到一般,再一般回到特殊”思想方法;归纳出由抽象到具体得到一般性结论,提升学生知识的类比、迁移能力,揭示数学问题的本质、透彻理解数学内涵,提高学习的有效性.

4.研究学生答题统计数据,关注学情变化.

答题数据是定态的,教学过程是动态的,如何透过枯燥的数据看出自身问题,教师不能局限于成绩数据、平均分等.而要透过大数据结论反观教学过程,让答题数据宝贵资源真正的服务于教学,对课堂教学的起到实质指导作用,由教学行为到教学理念的转变.教师从细节、从规范、从习惯处更加细致地了解学生,关注学情,理解学生,转变教学;在此基础上进行有效二次备课,学生理解了数学、教师升华了教学.

[1]黄健.回归本源突破难点[J].中学数学月刊,2014(4):23-25.

[2]陈春.对一道高考题的再探究[J].数学通讯,2012(1,2):66-67.