圆的两条性质的类比推广*

安徽省歙县中学(245200) 郑观宝

圆的两条性质的类比推广*

安徽省歙县中学(245200) 郑观宝

一、圆的两条性质

性质如图1,AB是⊙O:x2+ y2=R2的直径,直线AD、BC、CD分别与⊙O相切于A、B、T(动点),点G为直线AB上的定点(除直径端点),则(1)|AD|·|BC|=R2; (2)kGC·kGD为定值;

图1

证明(1)设切点T(x0,y0),则切线CD:x0x+y0y= R2(文[1]下同),于是

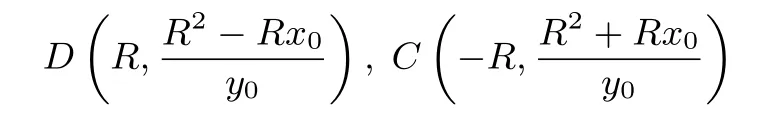
所以

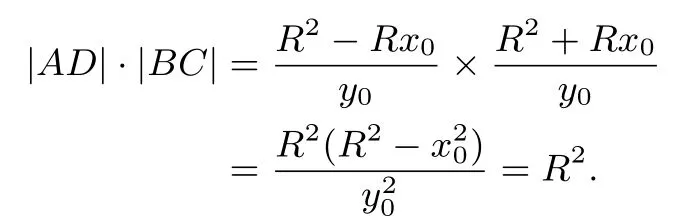
此性质还可用平面几何知识证明:连OT,OC,OD,容易证明

则

即OC⊥OD,所以Rt△AOD∽Rt△BCO,于是AD·BC= R2.

(2)设点G的坐标为(g,0)(g为常数)则

推论1当G为圆心O时,kOC×kOD=−1,即OC⊥OD.

推论2如图1,AB是半径为R的⊙O的直径,AD、BC分别与⊙O相切于A、B,直线l与这两条切线分别相交于C、D,且C、D在AB的同侧,若AD·BC=R2,则直线l与⊙O相切.

事实上,推论2是性质1的逆命题成立.

证明设|AD|=m,|BC|=n,则D(R,m),C(−R,n)故直线

则圆心O到CD的距离为

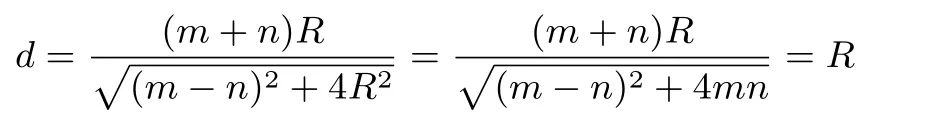
即直线CD与椭圆相切.综上所述,我们得到,直线CD与圆相切的充要条件为:点C、D在AB的同侧,且mn=R2.

二、在椭圆中的类比推广

图2

证明(1)设切点T(x0,y0),则切线

(2)设点G的坐标为(g,0)(g为常数)则

(为定值).

推论1当G为椭圆焦点时,kGC×kGD=−1,则F1C⊥F1D,F2C⊥F2D;

这是椭圆的一条重要性质.此性质还可以如下证明:连F2T,F2C,F2D,由于AD、BC、CD分别与椭圆相切于A、B、T,则

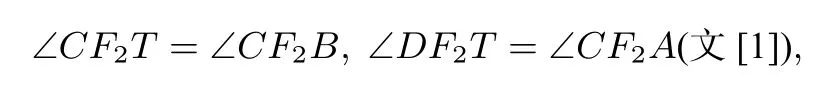
所以

即F2C⊥F2D.同理可证F1C⊥F1D.

推论2如图2,AB是椭圆的长轴,AD、BC分别与⊙O相切于A、B,直线l与这两条切线分别相交于C、D,且C、D在AB的同侧,若|AD|·|BC|=b2,则直线l与⊙O相切.

证明设|AD|=m,|BC|=n,则D(a,m),C(−a,n)故直线

说明这就是判断直线与椭圆相切的公式.

三、在椭圆中的再推广

图3

证明只要将推广1的证明过程中a2与b2的互换即可,限于篇幅,具体过程这里略去.

说明由于kGC×kGD=≠−1,所以GC、GD不可能相互垂直;

推论如图3,AB是椭圆的短轴,AD、BC分别与⊙O相切于A、B,直线l与这两条切线分别相交于C、D,且C、D在AB的同侧,若|AD|·|BC|=b2,则直线l与⊙O相切(限于篇幅,证明过程这里略去).

于是得到结论:直线CD与椭圆相切的充要条件为:C、D在AB的同侧,且|AD|·|BC|=a2.

推广23如图4,AB是椭圆=1(a＞b＞0)的任意一条固定的中心弦,直线AD、BC、CD分别与椭圆相切于A、B、T(动点),点G为直线AB上的定点,则 (1)|AD|·|BC|为定值;(2)仅当点G与点O重合时,kGC·kGD为定值.

图4

证明(1)设切点T(x0,y0),A(p,q),B(−p,−q),则切线

(2)当点G与坐标原点重合时,

若点G的坐标为(tp,tq)(t为非零常数),同上举反例,证明kGC×kGD的值不是常数.限于篇幅,这里略去.

四、在双曲线中的类比推广

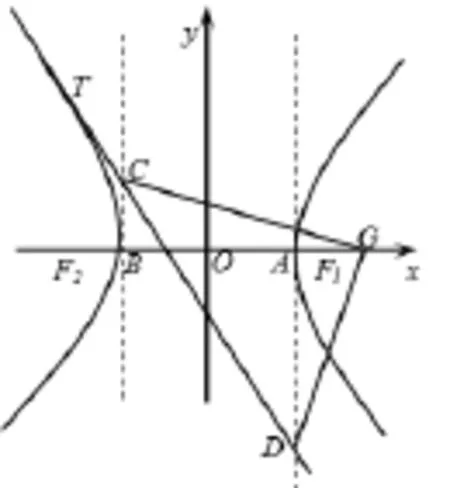
图5

证明只要将推广1的证明过程中b2的换成−b2即可,限于篇幅,具体过程这里略去.

推论1当G为双曲线焦点时,kGC×kGD=则F1C⊥F1D,F2C⊥F2D(这是双曲线的一条重要性质).

推论2如图5,AB是双曲线的实轴,AD、BC分别与双曲线相切于A、B,直线与这两条切线分别相交于C、D,且C、D在AB的异侧,若|AD|·|BC|=b2,则直线l与⊙O相切.

证明令|AD|=m,|BC|=n,不妨设D(a,−m),C(−a,n),故直线

即直线CD与椭圆相切.

综上所述,我们得到,直线CD与双曲线相切的充要条件为:点C、D在AB的异侧,且mn=b2.

推论3直线Ax+By+C=0(不为双曲线的渐近线)与双曲线=1(a＞0,b＞0)相切的充要条件是A2a2+B2b2=C2.

证明这里仅给B≠0情形的证明过程.在直线Ax+By+C=0中分别取x=−a,a,得

则直线l与双曲线相切的充要条件为

化简得A2a2+B2b2=C2.

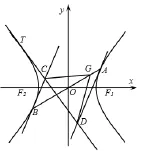
图6

限于篇幅,具体证明过程这里略去.

五、在抛物线中的类比推广

由于抛物线y2=2px(p＞0)是无心圆锥曲线,所以上述圆的第一条性质无法推广到抛物线中.但是,若将抛物线y2=2px(p＞0)看作中心在x正半轴的无穷远处,则圆性质的推论1可以推广到抛物线中.

推广5如图7,直线CT与抛物线y2=2px(p＞0)相切于点T(动点),F为焦点,则CF⊥CT.

推论1如图7,设直线l与y轴相交于点C,抛物线y2=2px(p＞0)的焦点为F,则直线l与抛物线相切的充要条件是l⊥CF.

推论2直线l:Ax+By+C=0与抛物线y2=2px(p＞0)相切的充要条件是B2p=2AC.

图7

[1]郑观宝.浅议圆的一条性质[J].数学教学研究,2006,10.

*本文系安徽省教育科学规划重点课题(课题编号:JG12316)成果.