Gergonne点在圆锥曲线中的推广

2016-12-23安徽省寿县第一中学232200梁昌金

中学数学研究(广东) 2016年7期

关键词：阿基米德平分切点

安徽省寿县第一中学(232200) 梁昌金

Gergonne点在圆锥曲线中的推广

安徽省寿县第一中学(232200) 梁昌金

一、提出问题

三角形中有众多的“巧合点”,如三角形的“五心”,而Gergonne(Gergonne,法国数学家,1771-1859)点亦是三角形中的“巧合点”之一,它有如下优美性质:

定理1(《数学通报》数学问题1741)如图1,△ABC的内切圆分别切边AB、BC、CA于点D、E、F,则AE、BF、CD三线共点.

图1

即连接三角形的顶点和内切圆与对边切点的直线交于一点,这个点称为Gergonne点.

证明:由圆的切线性质,知AD=AF,BD=BF,CE=CF,所以根据塞瓦定理的逆定理知,AE、BF、CD三线共点.

二、推广结论

笔者见到这个性质以后,惊喜万分,一个自然的想法浮现在眼前,Gergonne点能否推广到圆锥曲线中?经过笔者的研究,得到了肯定的答案.在给出推广结论和证明之前,我们先介绍一下圆锥曲线的阿基米德三角形及其性质,并证明这个性质.

圆锥曲线的阿基米德三角形:由圆锥曲线的弦及过弦的端点的两条切线所围成的三角形称为圆锥曲线的阿基米德三角形.

椭圆(双曲线)的阿基米德三角形性质:若△PAB为椭圆(双曲线)的阿基米德三角形,则OP平分切点弦AB(其中O为坐标原点).

抛物线的阿基米德三角形性质:若△PAB为抛物线的阿基米德三角形,过P作抛物线对称轴的平行线,则此平行线平分切点弦AB.

由于证明过程类似,笔者仅给出椭圆阿基米德三角形性质的证明.

图2

①当x0=0时,由椭圆对称性易知结论成立;

②当x0≠0时,设A(x1,y1),

B(x2,y2),则切点弦AB的方程为

联立

消去y,得

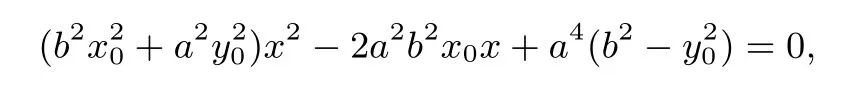
由韦达定理得

所以O,C,P三点共线,即OP平分切点弦AB.

综合①、②知,OP平分切点弦AB.

定理2若△ABC的三边AB、BC、CA(或其延长线)与椭圆分别相切于点D、E、F,则AE、BF、CD三线共点.

下面给出△ABC的内切椭圆情形的证明,外切椭圆情形类似可证.

证明:如图3所示,连接OA、OB、OC、OD、OE、OF、DE、EF、FD.由椭圆阿基米德三角形性质知,直线OA平分切点弦FD,直线OB平分切点弦DE,直线OC平分切点弦EF.于是S△AOD=S△AOF,S△BOD=S△BOE,S△COE=S△COF,故根据塞瓦定理的逆定理知,AE、BF、CD三线共点.

图3

定理3若△ABC的三边AB、BF、CA(或其延长线)与双曲线分别相切于点D、E、F,则AE、BF、CD三线共点.

证明过程类似定理2,此处从略.

定理4若△ABC的三边AB、BC、CA(或其延长线)与抛物线分别相切于点D、E、F,则AE、BF、CD三线共点.

证明:如图4所示,过A,B,C作轴的平行线,分别交DF于点P,M,N.由抛物线阿基米德三角形性质知,AP平分切点弦DF,BM平分切点弦DE,CN平分切点弦EF.所以DP=FP,

图4

则

根据塞瓦定理的逆定理知,AE、BF、CD三线共点.

三、赛题链接

例(2014年高中数学联合竞赛B卷一试第11题)如图5所示,已知椭圆Γ:A(−2,0),B(0,−1)是椭圆Γ上的两点,直线l1:x=−2,l2:y=−1. P(x0,y0)(x)＞0,y0＞0)是Γ上的一个动点,l3是过点P且与Γ相切的直线,C、D、E分别是直线l1与l2、l2与l3、l1与l3的交点.求证:三条直线AD、BE、CP共点.