追本溯源回归教材—浅论用真分式不等式,解决一类求和型数列不等式的证明问题

广东省开平市开侨中学(529300) 杨春传

追本溯源回归教材—浅论用真分式不等式,解决一类求和型数列不等式的证明问题

广东省开平市开侨中学(529300) 杨春传

在高考解答题中,常渗透数列与不等式证明的内容这个难点,在证明过程中,要适当地进行放缩,但放缩的范围较难把握,常常出现放缩后得不出结论或得到相反结论的现象.常规方法要求抓住题目的特点,掌握放缩技巧,并且还要根据不同题目的类型,采用恰到好处的放缩方法,才能把题解活.还要求学生掌握比较多的放缩技巧,这对学生来说,是很难做到的.但是如果我们追本溯源,回归教材,就会发现教材已经给出了很好的解决问题的方法.

人教版普通高中课程标准试验教科书选修4-5中有这样一个真分数不等式:已知0＜a＜b,m＞0,则它具有生动的现实情境:“糖水加糖变甜了”.其证明方法有分析法、综合法、反证法、放缩法、构造法等10多种证明方法,它不仅可以作为一个不等式证明的基本模型,很多高考题都可以用它来求解.下面我们利用精确放缩证明通项形如:且f(n)−a＞b＞0的求和型数列不等式的证明,希望能抛砖引玉,并说明求解高考题时可以化归为课本己解决的问题来求解.

一、真分数不等式的证明.

二、用真分数不等式精确放缩求和型数列不等式的原理.

进一步化简得

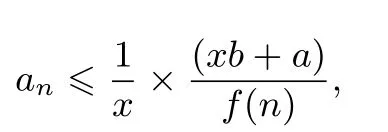
其中xb+a≤f(n)恒成立.它的化学意义是:通过x控制加糖量控制好糖水浓度.而在数学上,我们可以通过调整x的值进行精确放缩.

三、用真分数不等式精确放缩求和型数列不等式的应用举例.

例1已知数列{an}的前n项和Sn满足an+1= Sn+n+1(n∈N∗),且a2,a3+2,a4成等差数列.

(1)求a1;

(2)求数列{an}的通项公式;

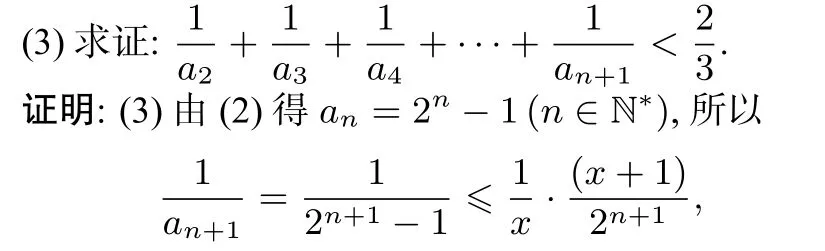
令

恒成立,从而

解得x≤3,取x=3得

如果本题想放缩得更精确,则可以保留第一项(越精确,保留的项数越多),从第二项开始应用真分数不等式,即令

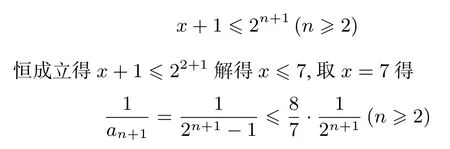
例2(2012年高考广东卷(理19))设数列{an}的前n项和为Sn,满足2Sn=an+1−2n+1+1,n∈N∗,且a1,a2+5,a3成等差数列.

(1)求a1的值;

(2)求数列{an}的通项公式;

例3(2014年佛山一模(理20))数列{an}、{bn}的每一项都是正数,a1=8,b1=16,且an、bn、an+1成等差数列,bn、an+1、bn+1成等比数列,n=1,2,3,···.

(1)求a2、b2的值;

(2)求数列{an}、{bn}的通项公式;

例4已知数列{an}的前n项和为Sn,且a1+2a2+ 3a3+···+nan=(n−1)Sn+2n(n∈N∗).

(1)求数列{an}的通项公式;

两式相减得

例5(2009年高考广东卷(理21))已知曲线Cn: x2−2nx+y2=0(n=1,2,···).从点P(−1,0)向曲线Cn引斜率为kn(kn＞0)的切线ln,切点为Pn(xn,yn).

(1)求数列{xn}与{yn}的通项公式;

又由真分数不等式得

同样的,像这种求积型的数列不等式的证明问题,可直接运用真分数不等式放缩求解.

通过以上例子的证明过程可以知道,高考中的不少难题,很多都可以化归为教材中已经解决的一些问题来解决.由于很多高考题,直接取自教材,或为原题、或为类题,或是课本概念、例题、习题的改编,或是教材中的几个题目、几种方法的串联、并联、综合与开拓,即便是少量的难题,也是按照课本内容设计的,只是在综合性、灵活性上要求较高.总而言之,我们在解决问题时,要学会“追本溯源,回归教材”.