对一道解几题的解法探究与辨析思考*

江苏省江浦高级中学(211800) 徐爱勇

对一道解几题的解法探究与辨析思考*

江苏省江浦高级中学(211800) 徐爱勇

1.问题背景

在解题过程中,对于同一道试题,从多个角度去分析探究,就会得到不同的启示,从而引出丰富多样的解法.因此,在进行解题教学时,我们不失时机地开展“一题多解”训练,通过广泛地联想,使学生的思维触角伸向不同的方向、不同的层次,这样不仅能巩固复习所学知识,而且能较好地培养学生思维的广阔性.

圆锥曲线是高中数学的一个重要内容,也是每年高考的一个必考点.在近些年的高考和模考中,出现了许多精彩的考题.又由于研究双曲线及抛物线的方法与椭圆有诸多相似之处,再考虑到江苏高考对椭圆的考试要求(B级)明显地高于双曲线(A级)和抛物线(A级),故而对与椭圆相关试题的命制成为各类考试的一个热点.

作为数学教师,我们应当站在更高的层次上来看待这些试题,通过对这些精彩试题研究,揭示它们的解法和算理,提升学生的兴趣,发挥其最大的教学功能.本文将对一道模考解析几何题展开解法探究、思维辨析和点滴思考,并能够引起广泛地关注,以期达到对“一题多解”有着较为全面的认识.

2.题目展示

(1)求椭圆的标准方程;

(2)设直线PF2的倾斜角为α,直线PF1的倾斜角为β,当β−α=时,证明:点P在一定圆上;

(3)设椭圆的上顶点为Q,在满足条件(2)的情形下证明: PF1+PF2=PQ.

(3)下面着重研究第(3)问.

3.解法探究

3.1 思维基点1—从代数方程出发

解法1因为

图1

3.2 思维基点2—从正弦定理出发

在Rt△PQR中,

3.3 思维基点3—从余弦定理出发

3.4 思维基点4—从托勒密定理出发

解法4托勒密定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.根据题意,得

又因为

所以PF1+PF2=PQ.

3.5 思维基点5—从几何构造出发

解法5因为QF1=QF2,所以∠QPF1=∠QPF2= 60°,在PQ上截取PM=PF2,PN=PF1,△PF2M与△PF1N是等边三角形,易证△F1QN≌△QF2M,所以QN=F2M,PN=PF1,所以PF1+PF2=PQ.

图2

4.思维辨析

4.1 从方程的角度出发,增加解题必胜的信念

方程思想是通过分析问题中的变量间的等量关系,从而建立方程(或方程组),或运用方程的性质去分析、转化问题,使问题易于解决,其精髓是方程(组)的确定.

根据本题所给的条件,我们不难得出如下的方程:

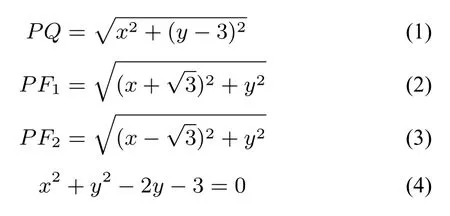
而对于这四个方程,我们瞄准一个目标(PF1+PF2=PQ),并且紧紧抓住问题中的两个变量(x,y),那么,只需对方程(4)做合理变形即可.我们的学生在应试中对解析几何的运算存在较大地盲目性,在解题的过程中的目标意识不够明确.究其原因,应该是在平时的训练中缺乏对字母运算的“方程意识”.鉴于此,我们在平时的解几教学环节中,加强方程思想的渗透,势必会增加解题必胜的信念.

4.2 从函数的角度出发,提高解题转化的能力

函数思想是运用运动和变化的观点,集合与对应的思想,去分析和研究数学问题中的数量关系,建立函数关系或构造函数,再利用函数的图像或性质去分析问题,转化问题,从而使问题获得解决,其精髓是构造函数.

根据前面的分析,我们较容易得到这样一条清晰的解题流程:

实践证明,思维水平的提升将极大地推进学生运算技能的提高.解题教学中适时揭开“技巧”的神秘面纱,揭示其蕴含的思想方法,对于提高学生的解题能力大有裨益.

4.3 从表达的角度出发,丰富解题不同的方法

解题过程的繁简程度是决定解题成败的重要因素.同样的思路,不同的过程,解题效果会迥然不同.到目前为止,我们已经捕获这样的关键信息—表达好点P.由于点P在圆弧x2+y2−2y−3=0(y＜0)上,那么,我们在表达点P的过程中,就有了多种形式,从而产生了不同的策略.

策略1(详见解法1):

策略2(详见解法2、3):

策略3(详见解法4、5):

4.4 从辩证的角度出发,审视解题活动的意义

笔者在指导学生解题时,首先强调通性通法,当然也不忽视奇思妙解.尽管有时思维受阻,抓耳捞腮,但从来没有半途而废,一点点积累,一次次回味,承秉多想少算,讲究解题高效率,因此经常性地收获着“意外”的惊喜.解法5所采用的“构造法”,就是一个“意料之外,情理之中”的产物.

当下,在淡化技巧的环境下谈奇思妙解,是否为唱反调?笔者认为,任何观念都有各自流行的时代,回顾过度追求技巧的昨天,也许今天就该流行通性通法,但如果过度偏向一方,只会走极端,这种极端不是解决具体问题中的极端,而是观念上的极端.

5.点滴思考

数学学习强调探究,也强调一题多解,通过多方位、多角度、多途径、多方式观察和解决问题,能够激发学习数学的热情,能够进一步增强对数学基本概念的理解,能够提高处理数学问题的能力,能够指引我们找到多题一解的简捷通法.因此,我们在平时学习数学的过程中,要善于多视角、多方面、全方位地分析思考问题,以达到拓宽思路、提高解题能力、发展创新思维的目的.

同时,对学生实施思维训练的操作过程中,还要注意以下几个环节:

(1)问题(课题)应具有探究性、可创造性;

(2)在启发性思维的过程中,应注意教师的主导与指导作用;

(3)给学生充分的时间进行发散性思维训练;

(4)已达成解决问题方法的共识后,教师应加以总结,以获得理性认识;

(5)加强反馈训练,以深化理性认识.

可见,不同的视角,产生不同的解题思路.通过集中展示,更有利于学生感悟解决问题的通性通法,有效提高举一反三、触类旁通的能力.在此过程中,学生容易感受到:解题教学不要图多求难,重视引导学生多角度审视,全方位探究,复习才能收到实效.

[1]韩雪华.浅析解析几何运动变化型问题中的参数选取[J].中学数学月刊,2013,8,55—56.

[2]徐爱勇.习题讲评中也要关注“正确下的猫腻”[J].中学数学月刊,2015,4,64—66.

[3]徐爱勇.对一道模考题多维辨析与深层思考[J].中学数学教学参考,2015,7,32—34.

*本文系江苏省教育科学规划十二五课题“生态课堂观下分层自主学习模式的建构研究”(批准文号:201303LX)阶段性研究成果.