陀螺加速度计线振动台进动整周测试方法

孙 闯，任顺清，师少龙，曾 鸣

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150080）

陀螺加速度计线振动台进动整周测试方法

孙 闯，任顺清，师少龙，曾 鸣

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150080）

为了提高陀螺加速度计在线振动条件下的标定精度，提出了陀螺加速度计在线振动台上的进动整周期的测试方法。该方法将陀螺加速度计正倒置安装后，在静态和线振动状态下分别测量陀螺加速度计进动整周期中的相关时间数据，计算出陀螺加速度计进动整周期的平均角速率，通过平均角速率与陀螺加速度计模型输出间的积分关系，推导出了陀螺加速度计在线振动台上的标定误差模型，辨识出了加速度计的零偏、标度因子、二次项系数和三次项系数。该方法抑制了陀螺加速度计输出的平均角速率误差，能够提高陀螺加速度计在线振动台上测试的精度。最后进行了算法验证，验证了该方法能够准确的辨识出加速度计的各项误差模型系数，辨识精度达到10-7，提高了陀螺加速度计在线振动台上的标定精度。

陀螺加速度计；误差模型；线振动台；标定

陀螺加速度计广泛应用于导弹与火箭运载体上，它的使用精度直接决定了飞行器的制导精度，而其标定测试精度将直接影响其使用精度[1-2]。目前，关于陀螺加速度计的标定测试大体分为重力场下的试验与高g条件下的试验[3]。

以往在重力场下的静态翻滚试验多利用分度头、三轴台等测试设备进行[4-5]，由于重力加速度的大小与方向可以精准测出，因此对加速度计的静态性能参数测试精度较高，试验成本较低，操作简单，但不能充分激励高阶项误差[6]。由于飞行器通常的工作条件是大于1g的复合力学环境，传统陀螺加速度计的重力场标定与真实的工作环境存在偏差，有些误差项没有进行完全激励和标定，从而影响了其使用精度。在高g与线振动条件下的标定，大多通过精密离心机、火箭橇和线振动台完成，精密离心机能在高过载条件下激励陀螺加速度计的高阶误差项系数并加以辨识。但离心机试验成本较高，实验过程中干扰误差多，试验周期较长[7-8]。火箭橇则通过较长的轨道产生高g的冲击加速度，用以模拟实际使用中的由加速度、角加速度与角速度等条件构成的复合环境，但使用成本更高，测试研究较少[9]。由于线振动台可以产生正弦的输入比力，因此可以测试陀螺加速度计的全量程性能[10]。陀螺加速度计在线振动台上的标定，目前国内外研究较少，文献[11-12]给出了利用线振动台对线加速度计模型的非线性系数进行标定的方法，通过振动整流减少标定误差，但标定精度受线振动台的运动特性影响。

本文设计了一种陀螺加速度计的振动台测试方法，通过振动台产生高g的正弦线振动测试环境，对陀螺加速度计的高阶误差项系数进行激励，利用陀螺加速度计的整周期进动定角测时，计算得到平均进动角速率，抑制了陀螺加速度计输出装置误差对测试误差的影响，提高了陀螺加速度计的标定精度。该方法既解决在普通重力场条件下无法模拟真实工作环境而产生的偏差，又相比离心机的测试方法缩短了试验周期，降低了试验成本。

1 系统简介

图1 测试系统图Fig.1 The measurement system

测试系统如图1所示，整个测试系统由高精度线振动台，线振动台测位系统、高精度计时计数系统和陀螺加速度计等组成。其中，高精度线振动台包括工作台、测头和提供角速度的曲柄等，可以提供0.1g～10g的精密谐波加速度。计时计数系统主要包括高精度计时器与高精度计数器，高精度计时器上的CPU时钟频率为2.9 GHz，周期约为340 ps，因此可提供精度达到10-7s、误差小于50 ns的时间计数。高精度的计时器与陀螺加速度计输出系统和线振动台测试系统连接，提供准确的线振动台工作时间与陀螺加速度计的进动周期时间。本文用于测试的陀螺加速度计进动一周的脉冲数为16 384，高精度计数器则通过记录陀螺加速度计上正负脉冲通道的脉冲数来确定进动周期。

2 误差标定模型

在理想状态下，线振动台的工作台和陀螺加速度计的摆轴 PA始终处于水平位置，加速度计在摆轴上的比力分量为零，即aPA=0。陀螺加速度计的输出轴OA与摆轴正交且处于水平位置，因此，aOA=0。

由陀螺加速度计在理想情况下的安装位置可知，由于aPA和aOA为0，进动角速度输出方程可表示为

式中：α˙为进动角速率，单位为 rad/s；aIA为输入轴比力；ml为绕内框架轴的摆性，单位为kg· m；H为角动量，单位为2kg· m/s。

如果工作台始终保持水平，当陀螺加速度计输入轴垂直安装在工作台上时，虽然可以认为在OA轴的比力分量为零，但地球的自转角速率会对加速度计输出产生影响，因此需要进行补偿。同时考虑陀螺加速度计在高g环境下工作时，输出方程需要高阶数的误差项来弥补大比力输入对输出的影响，因此需要三次项误差系数，最终加速度计输出方程为

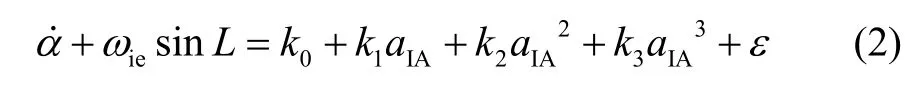
式中：k0、k1、k2、k3为误差项系数；ωie为地球自转角速度，单位为rad/s；L为测试所在地纬度；ε为随机误差。

根据振动台的原理可知，当振动台以加速度幅值A，角速度ω工作时，在t时刻产生的比力为

式中：A=ω2A0，A0为振动台的振动幅值，单位为m。因此当陀螺加速度计输入轴垂直向上安装时，其输出误差模型为

3 陀螺加速度计的标定方法

为了抑制陀螺加速度计输出装置误差的影响，下面将采用整周进动的方法，测试方法流程图如图2所示。

图2 测试方法流程图Fig.2 Flow chart of the measurement method

将陀螺加速度安装在水平的工作台上，当线振动台和陀螺加速度计稳定工作后启动计时与测位系统，测量系统的工作状态与工作时长，设定零时刻，至线振动台的第1 次过振动零点的时间间隔为t1。

试验用陀螺加速度计的输出单位为^/s，其进动一周的脉冲所装订的脉冲为16 384^，进动Nt周则装订脉冲为16 384Nt。当加速度计的脉冲值达到设定值时，记录进动整周的测量总时间，设为 Tm。进动 Nt周测量完成后，再测量至下一次线振动过零点的时间间隔为t2，最后通过测位系统记录振动台的振动周期数NP，其中NP为t1至t2+Tm时间间隔内振动台振动周期。显然t时刻振动台的振动加速度为。设时间为，当陀螺加速度计正置安装时，各个时间节点与陀螺加速度计输入比力关系如图3中所示。

为了能准确辨识出公式(4)中的4个误差项系数，本文在陀螺加速度计输入轴分别垂直于振动台朝上或朝下，振动台工作与不工作的情况下设计了4次测试：

图3 陀螺加速度计比力随测试时间变化关系Fig.3 Variation of PIGA’s specific force with testing time

1）当陀螺加速度计输入轴向上垂直安装在振动台上，设进动Nt整周的测量总时间为Tm1，考虑地球自转，根据公式(4)，振动台振动时，陀螺加速度计的瞬时进动角速率为

在Tm1时间内的平均进动角速率为

显然，公式(6)等号右边第2项为振动运动的整周积分，则有：

2）当陀螺加速度计输入轴朝上，振动台不工作时，即A=0，设进动Nt整周的测量总时间为Tm2，得到平均进动角速率：

3）采用同样的方法，将陀螺加速度计的输入轴朝下，设进动整周的测量总时间为Tm3，线振动台的第1次过零点的时刻为t3，进动Nt周测量完成后，测量下一次线振动过零点的时刻为t4+ Tm3，设t3至t4+ Tm3时间间隔内振动台振动了Nq周，时间为振动台振动时，陀螺加速度计的瞬时进动角速率为

在Tm3时间内的平均进动角速率为

将公式(11)展开计算整理得到：

4）当陀螺加速度计输入轴朝下，振动台不工作时，即A=0，设进动Nt整周的测量总时间为Tm4，陀螺加速度计平均进动角速率为

最后，综合4次测试结果，联立式(8)(9)(12)(13)，整理成矩阵形式，可得到：

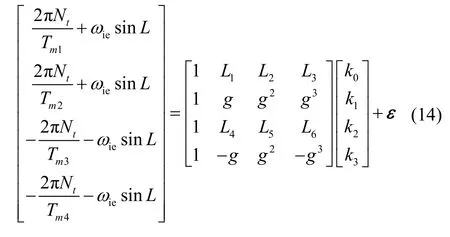
式中：ε矩阵为干扰矩阵；信息矩阵Ф和输出矩阵Y含有参数A 、t1、t2、t3、Tm1、Tm2、Tm3等可以通过测试系统准确的进行测量。基于最小二乘原理对公式(14)进行参数辨识，可辨识出k0、k1、k2、k3系数。

4 算法验证与误差分析

下面通过具体的算例来验证该方法的有效性。设线振动台的数据为ω=2πf ，振幅A0为0.03m，因此地球自转的角速度为，以北京的纬度为例，即 L=39.9°，地球重力加速度g=9.801 609 3 m/s2；设定陀螺加速度计进动周期为 Nt=50，零偏、标度因子、二次项和三次项误差系数分别为：计时系统测量的时间和振动台振动周期数为：Np1=4484，t1=0.0573s，Tm1=560.529 052 5 s，t2= 0.028 337 0 s，Tm2=560.928 847 7 s，Np2=4 494，t3=0.047 590 0 s，Tm3=561.778 524 1 s，t4=0.019 066 0 s，Tm4=561.161 299 0 s。

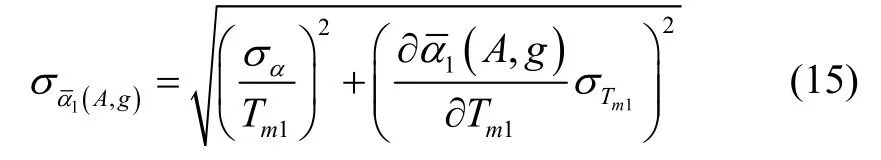
由于采用对陀螺加速度计的脉冲进行计数的形式来测量进动周期，假设测试系统脉冲计数误差为1脉冲，则进动角度的测量不确定度等于相邻脉冲信号之间的进动角度为。由于测试系统计时器的时间精度可以达到10-7s，因此在公式(15)中：不确定度计算可忽略这部分。

最终可以得出4组试验下陀螺加速度计的平均角速率不确定度，分别为：单位为rad/s。通过计算结果可以看出，输出角速度的不确定度均达到了。当纬度角的测量精度为0.1°时，可算出ωiesinL的测量精度为。根据计算结果可以看出，整周期的陀螺加速度计标定其标定的测试输出精度理论上都可以达到10-7的精度要求。

通过计算结果可以看出，本文所提出的陀螺加速度计正周期标定方法均可以达到 10-7的标定精度要求。对于高阶误差项系数的标定精度甚至能达到10-9。

根据各项参数的设定值，计算出公式(14)中输出矩阵Y中的各项值。考虑加入10-8量级的系统随机扰动时，最小二乘辨识公式为

通过公式(18)对误差项系数进行辨识的结果如表1所示，从中可看出，本方法对于各误差项系数的辨识都能达到较高精度，绝对误差均在10-7。基于最小二乘的陀螺加速度计辨识对于三阶项的辨识相对误差较大，分析其原因主要有以下几点：首先，利用迭代方法求解出的设定时间参数本身存在着计算偏差；其次，本文的算法验证时的随机误差计算为10-8，对于10-7量级的三阶辨识影响更大；最后由于本文基于 4组试验数据对误差模型系数进行辨识，因此通过增加试验组数和采样数据数，高阶项辨识误差也会随之减小。

表1 误差项系数辨识结果Tab.1 Identification results of error coefficients

5 结 论

本文分析了陀螺加速度计在线振动台上的测试原理，根据陀螺加速度计进动角速率与输出之间的积分关系，建立了陀螺加速度计在线振动台上的测试系统，提出了通过测量进动整周的输出数据来减小输出误差的测试方法，分析了将加速度计正倒置安装，静态与线振动4种状态下加速度计的输入输出模型。通过仿真对算法进行了验证与误差分析，结果表明：该方法理论上对于各个误差系数的测量与标定精度均可以达到10-7以上；该方法可以通过较少的数据准确地辨识出陀螺加速度计的零偏、标度因子、二次项系数和三次项系数。同时，由于本文是通过计算平均角速率而减少输出误差，主要误差源为陀螺加速度计的单位脉冲角位置当量，当增加测试时间后，输出平均角速率的误差将得到抑制，可以充分地以时间取得更高精度的测试结果。进动整周期相较于振动整周期的方法，提高了陀螺加速度计输出的平均进动角速率的精度，也将未振动到整周的时间参数考虑进来消除了未振动到整周时所产生的误差，提高了测试精度。

（References）：

[1]Zhou Yuan, Zhang Jin-yun, Yan Lu, et al. Directional multi-position calibration of PIGA of inertial platform system[C]//22nd Saint Petersburg International Conference on Integrated Navigation Systems. Saint Petersburg,Russia, 2015: 292-297.

[2]Li Shu-sheng, Zhong Mai-ying, Zhao Yan. Accelerometer error estimation and compensation for three-axis gyrostabilized camera mount based on proportional multipleintegral observer[J]. Science China Technological Sciences,2014, 57(12): 2387-2395.

[3]Kau D S, Boutelle J, Lawdermilt L. Accelerometer Input axis angular acceleration sensitivity[J]. IEEE Aerospace and Electronic Systems Magazine, 2005, 14(13): 449-456.

[4]Pan Jian-ye, Zhang Chun-xi, Cai Qing-zhong. An accurate calibration method for accelerometer nonlinear scale factor on a low-cost three-axis turntable[J]. Measurement Science and Technology, 2014, 25(2): 1-7.

[5]Gao Yang, Qin Ran, Guan Chen-qiu, et al. Development of data acquisition system for micro-accelerometers′dynamic centrifuge test[J]. Key Engineering Materials,2013, 562-565(3): 214-221.

[6]Verma P, Gopal R, Arya, Sandeep K. Analytical modeling and simulation of a 2-DOF drive and 1-DOF sense gyro-accelerometer[J]. Microsystem Technologies, 2013,19(8): 1239-1248.

[7]王世明, 任顺清, 王常虹. 在反转平台离心机上标定陀螺仪的误差模型系数的方法[J]. 中国惯性技术学报,2012, 20(5): 625-630.Wang Shi-ming, Ren Shun-qing, Wang Chang-hong. Calibration of gyro error model coefficients on precision centrifuge with counter-rotating platform[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 625-630.

[8]Ren Shun-qing, Wang Shi-ming. Impacts of installation errors on the calibration accuracy of gyro accelerometer tested on centrifuge[C]//2013 2th International Symposium on Instrumentation and Measurement, Sensor Network and Automation. Toronto, Canada. 2013: 914-918.

[9]董雪明, 何懿才, 关伟. 加速度计校准技术综述[J]. 计测技术, 2014, 34(4): 5-9.Dong Xue-ming, He Yi-cai, Guan Wei. Review of linear accelerometer calibration techniques[J]. Metrology &Measurement Technology, 2014, 34(4): 5-9.

[10]鲁金瑞, 任顺清, 王常虹. 振动整流法辨识加速度计非线性误差模型系数[J]. 仪器仪表学报, 2013, 34(9): 2130-2136.Lu Jin-rui, Ren Shun-qing, Wang Chang-hong. Identification method of accelerometer nonlinear error model coefficients with vibration rectification[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2130-2136.

[11]Std 1293-1998. IEEE standard specification recommended format guide and test procedure for linear single-axis,nongroscopic accelerometers[S].The Institute of Electrical and Electronics Engineers,1998.

[12]中国人民解放军总装备部. 单轴摆式伺服线加速度计试验方法[S]. 中华人民共和国国家军用标准, FL 6615, 2004.General Armaments Department of the People′s Liberation Army. Test methods for single-axis pendulous servo linear accelerometer[S]. The National Military Standard of the People’s Republic of China, FL 6615, 2004.

Measurement method for PIGA precession during integer periods on linear vibration table

SUN Chuang, REN Shun-qing, SHI Shao-long, ZENG Ming
(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150080, China)

In order to improve the calibration precision of PIGA (pendulous integrating gyro accelerometer)on linear vibration table, a measurement method for PIGA precession during integer periods on linear vibration table is proposed. The concerned integral time data of the PIGA precession within integer periods under the vibration state and the static state are measured while the PIGA’s input axis is installed on linear vibration table straight upwards and downwards respectively. The corresponding average precession angular rates of PIGA are calculated, and the calibration error model of the PIGA on a linear vibration table is derived by the relationship between the average precession angular rates and the model outputs of the PIGA. The error model coefficients, including the bias, the scale factor, the second-order coefficient and the third-order coefficient, are identified finally. By this testing method, the precession angular rate error of the PIGA is suppressed, and the accuracy of the test on linear vibration table is improved. Simulation results show that the method can accurately identify the error coefficients of PIGA, and the identification precision reaches 10-7,which improves the calibration precision of PIGA on linear vibration table.

pendulous integrating gyro accelerometer; error model; linear vibration table; calibration

V241.5+31

A

1005-6734(2016)05-0672-05

10.13695/j.cnki.12-1222/o3.2016.05.020

2016-07-07；

2016-09-20

装备预研基金项目（9140A09030313HT01121）；国家重大科学仪器设备开发专项（2013YQ310737）

孙闯（1989—），男，博士研究生，从事惯性技术研究。E-mail: sun489495923@163.com

联 系 人：任顺清（1967—），男，教授，博士生导师。E-mail: renshunqing@hit.edu.cn