从共振衰减响应中提取微机械陀螺的骨架曲线

魏玉淼，董永贵

（1. 清华大学 精密仪器系 精密测试技术及仪器国家重点实验室，北京 100084；2. 火箭军工程大学 202教研室，西安 710025）

从共振衰减响应中提取微机械陀螺的骨架曲线

魏玉淼1,2，董永贵1

（1. 清华大学 精密仪器系 精密测试技术及仪器国家重点实验室，北京 100084；2. 火箭军工程大学 202教研室，西安 710025）

为测量微机械陀螺的非线性特性，研究了一种从共振衰减响应信号中提取骨架曲线的方法。采用Hilbert变换处理共振衰减信号，对所得到的瞬时幅值及瞬时频率曲线进行奇异谱分析，滤除信号中噪声引起的非理想波动，从而得到清晰易辨的骨架曲线，解决了基于Hilbert变换的非线性辨识方法对噪声敏感的问题。针对Duffing系统的数值仿真结果表明，这种方法比FREEVIB方法具有更好的抗噪声性能。对一种环型振动微陀螺进行了实验测试，所得到的骨架曲线、阻尼曲线以及频率响应曲线与传统扫频方式的测量结果有良好的一致性。作为一种通用测试手段，这种方法同样适用于其他微机械谐振元件动力学特性的实验测试。

微机械陀螺；非线性特性；Hilbert变换；骨架曲线；奇异谱分析

微机械谐振器是基于谐振原理的 MEMS测量系统的重要组成部分，作为一类典型敏感元件，已广泛应用于微机械惯性传感器、谐振式压力传感器等领域。采用微电子技术和硅微加工工艺制作的微陀螺具有尺寸小、重量轻、成本低廉等优点，但其谐振器相对于宏观尺寸的机械振动系统更容易呈现出非线性动力学特性[1-2]。为获得更高的检测灵敏度，通常要求驱动模态具有较大的振幅，这有利于提高输出信号的信噪比。然而，谐振器的振动幅值接近甚至处于非线性区域时，非线性效应的影响增加会导致谐振器工作频率不稳定，系统的整体性能反而会因此而降低[3-4]。因此，针对微谐振器非线性动力学特性的研究成为近年来这一领域的热点[5-8]。

目前，非线性动力学特性的测试主要有正弦波扫频和自由衰减振荡两种方法。正弦波扫频法通过不同激励幅值下的频响曲线表征系统的非线性特性[9]。由于需要进行多次扫频，该方法操作过程复杂而繁琐。自由衰减振荡方法通过信号处理技术从共振衰减信号中提取出系统的非线性信息，是一种无参数模型的估计方法[10-11]。在这方面的研究中，以Feldman M提出的FREEVIB方法最为典型。采用Hilbert变换提取共振衰减响应信号中的瞬时模态参数，可有效实现系统的骨架曲线、阻尼曲线等非线性特性的辨识[11-13]。针对 Hilbert变换计算结果的噪声敏感问题，Peng Z K[14,15]、Wang C[16]分别利用多项式调频小波变换和小波脊线法从共振衰减信号中提取非线性系统的响应特性，数值仿真结果表现出较好的抗噪能力。

总体来看，由于Hilbert变换对噪声非常敏感[12-13]，基于自由衰减振荡与Hilbert变换的研究中，多以理论分析和数值仿真验证为主，工程应用实例较少。针对微陀螺、微加速度计等工作频率较高，Q值较大的谐振器的实例研究，尚未见相关报道。

奇异谱分析（Singular Spectrum Analysis, SSA）是一种数据驱动的自适应分析方法，不仅适用于分析常见的平稳信号，而且对非线性、非平稳信号也有较为理想的处理效果。SSA可以从含噪时间序列中准确地提取出各种特征信息，分离出趋势项、周期项、噪声等成分。与传统的基于频率特性的滤波方法相比，SSA在保留原始信号时域特征方面具有很好的优势。近年来，在健康医疗[17]、大地测量[18-19]、故障诊断[20]、非线性动力学等领域得到广泛应用。

本文以 MEMS环陀螺为研究对象，采用 Hilbert变换从共振衰减响应信号中提取出瞬时幅值（Instantaneous Amplitude, IA）和瞬时频率（Instantaneous Frequency, IF）。然后使用SSA算法消除IA和IF中的非理想波动，得到清晰易辨的骨架曲线、阻尼曲线及幅频曲线等非线性特征信息，解决了基于Hilbert变换的辨识方法的噪声敏感问题。测试结果与扫频法的实验结果一致，证明了这种方法的有效性。

1 原理及仿真分析

单自由度二阶动力学系统受到正弦脉冲激励时，其动力学方程可表达为

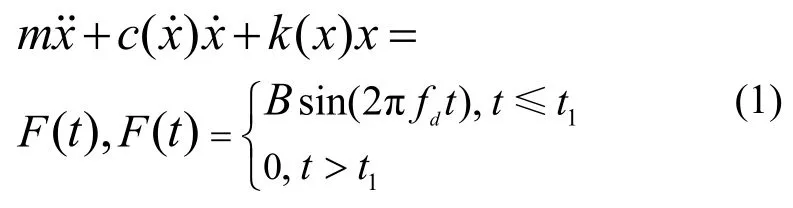
式中：m为模态质量；c( x˙)和k( x)分别为阻尼和刚度系数；F(t)为激励信号；B和fd分别表示激励幅值和频率；t1为正弦脉冲信号的宽度。t＞t1时，正弦脉冲激励停止，系统进入自由衰减振荡状态。

假定研究对象为高频低阻尼的 Duffing系统，模态质量为m=10-7kg。阻尼系数与振动幅值无关（线性阻尼），取为；刚度系数则与振动幅值有关，取为N/m（“软弹簧”特性的非线性刚度）。激励脉冲幅值和频率分别选为B=0.20N和fd=20kHz。t1取0.8s，采样频率 fs=1MHz，仿真总时间为 1.6s。利用 Matlab中的ode45求解器计算出系统共振衰减信号的时域波形如图1所示。

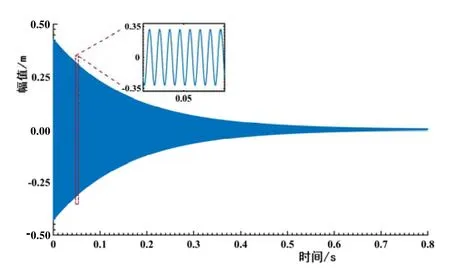
图1 仿真系统的共振衰减响应Fig.1 Resonance decay response of the simulated system

对于图1所示共振衰减响应信号x(t)，采用FREEVIB方法[11-13]获取系统非线性特性的处理过程如下：

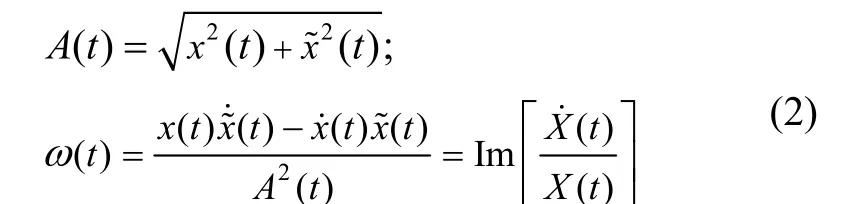
步骤 2 通过式(2)计算得到的瞬时幅值 A(t)、瞬时角频率ω(t)及其导数，估计出系统瞬时频率 f0(t)和阻尼系数h0(t)：

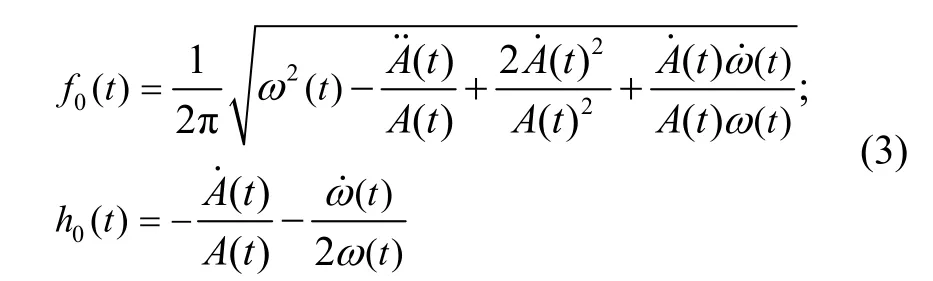
步骤3 采用低通滤波器对f0(t)、A(t)和h0(t)等进行平滑处理，得到f0(t)LPF、A(t)LPF以及h0(t)LPF，便可获得分别以f0(t)LPF、h0(t)LPF为横坐标，A(t)LPF作为纵坐标的骨架曲线和阻尼曲线，同时估计出频率响应曲线（Frequency Response Function, FRF）。

为模拟实测情况，向图1中的信号添加噪声，得到一组不同信噪比（SNR）下的共振衰减信号。使用FREEVIB方法分别进行处理，结果如图2所示。可以看出，FREEVIB方法能从理想信号中准确地提取出系统的骨架曲线以及阻尼曲线，估算出的FRF曲线清晰而规则。当SNR为70dB时，计算得到的骨架曲线上半部分与理论值能较好吻合，底部则出现了一定的偏离，阻尼曲线以及FRF曲线估计值均出现了明显波动。SNR降至50dB后，处理结果整体出现明显偏移，难以真实反映系统的非线性特性。

分析图2可知，骨架曲线以及FRF曲线的偏移主要是由于瞬时频率f0(t)LPF的估计结果（图2b）偏离理论值所导致。FREEVIB方法采用的是基于频率特性的低通滤波器，应该是导致瞬时频率出现较大波动的主要原因。与此相比，奇异谱分析（SSA）[17-20]能够在时域上准确提取出时间序列的变化趋势，可弥补频域滤波方法的这一缺陷。

奇异谱分析包含嵌套、SVD分解、分组、对角平均以及重构等处理过程。对于一维时间序列{y(i),i=1,2, ...,N}，首先通过嵌套得到Hankel型轨迹矩阵Y：

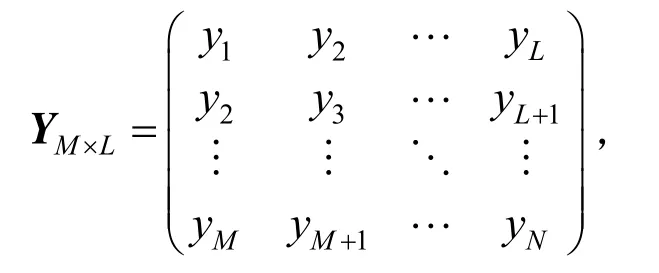
其中，L为选取的窗口长度，M=N-L+1。对YM×L进行奇异值分解（SVD），从而得到L个特征值及相应的特征向量U和V。其中表示第r个主成分。根据贡献率对各主成分进行分类重组，分别对应原时间序列中的各种特征分量。经对角平均化处理，并重构成一组时间序列，即

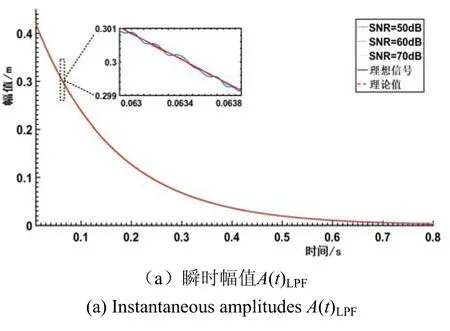
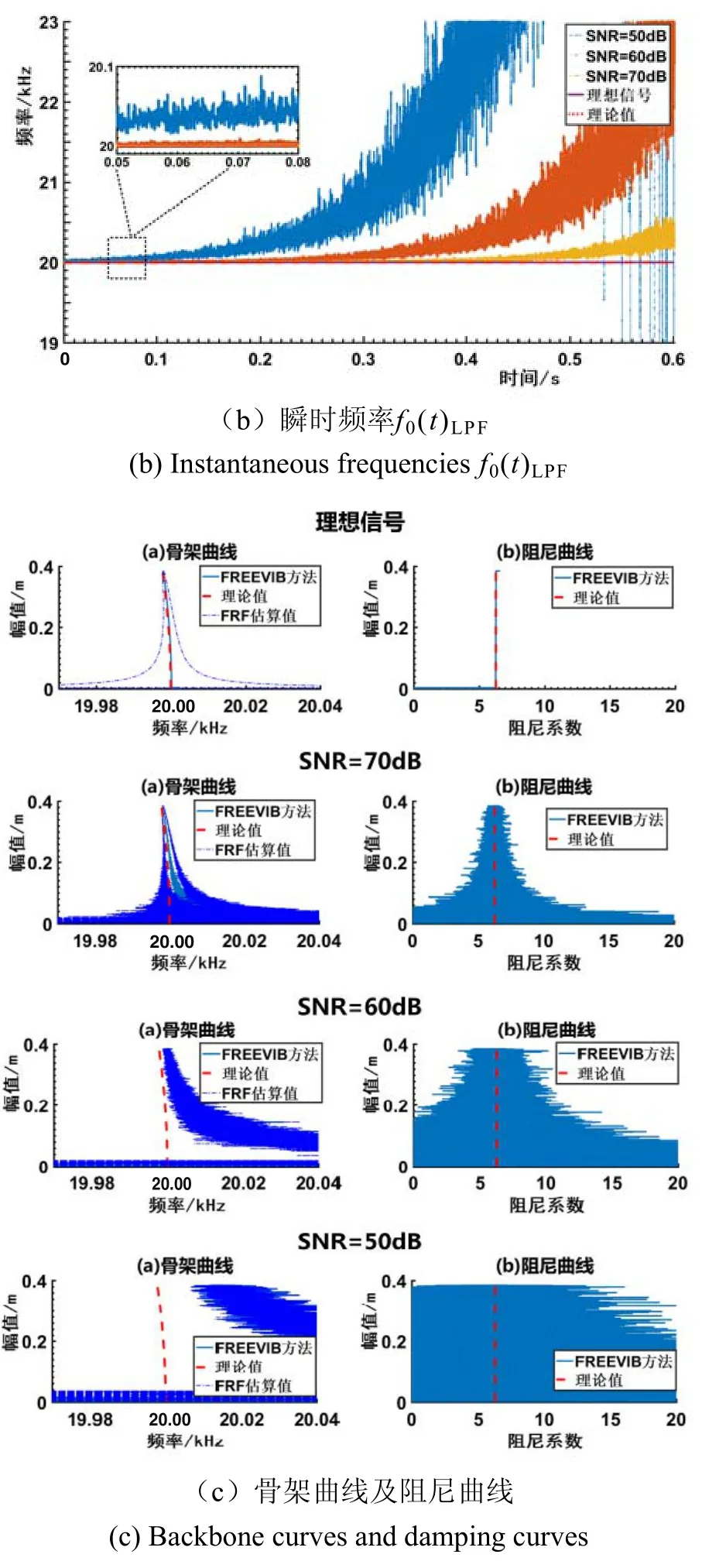
图2 不同SNR条件下FREEVIB法得到的计算结果Fig.2 Results corresponding to different SNRs obtained by FREEVIB method

可实现信号中趋势项、周期项、噪声等成分之间的分离。

引入SSA算法后的FREEVIB处理过程调整为：

步骤1 通过Hilbert变换提取共振衰减信号x(t)的瞬时幅值A(t)、瞬时相位θ(t)：

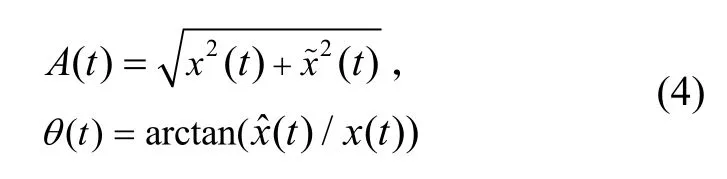
步骤3 使用A(t)SSA、f(t)SSA及其导数对阻尼系数h(t)进行估计，并根据A(t)SSA、f(t)SSA和h(t)计算出festd(t)[21]，进一步获得FRF曲线：

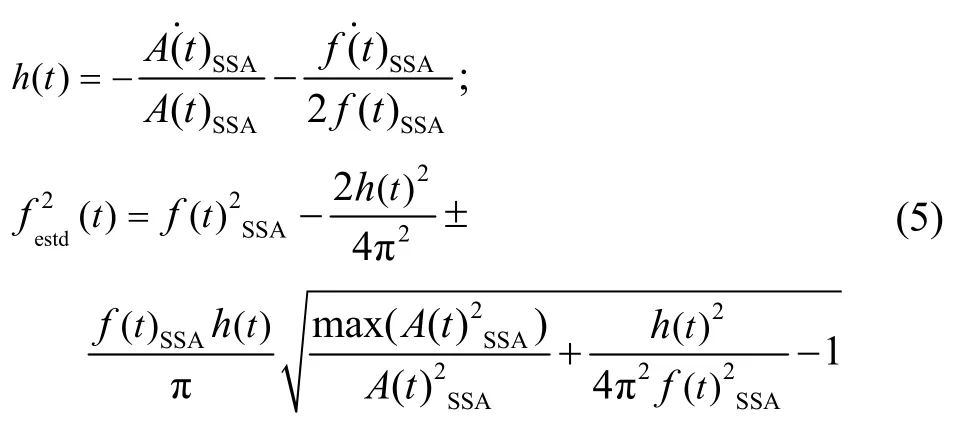
采用改进后的方法对上述不同 SNR下的共振衰减信号进行处理，SSA算法的窗长L均取为800。以SNR为50dB的共振衰减信号为例，对瞬时频率进行SSA处理。前5个主成分PC1～PC5的贡献率分别为82.643%、0.071%、0.071%、0.069%、0.068%。图 3给出了瞬时频率f(t)（图中的IF）的计算结果，以及IF经SSA处理后，由前5个主成分PC1～PC5重构得到的信号，从图中可以看出，PC1反映了原始信号IF在谐振频率（约20kHz）附近的变化规律，而PC2～PC5则主要反映 IF中高频成分的变化情况。因此，通过PC1即可提取出所需瞬时频率IF的变化趋势。也就是说，采用PC1的重构信号作为f(t)SSA，便可消除噪声引起的非理想波动。瞬时幅值的处理过程与此类似，也通过PC1重构得到A(t)SSA。按照相同的方法，对其余共振衰减信号进行处理，得到的计算结果如图4所示。

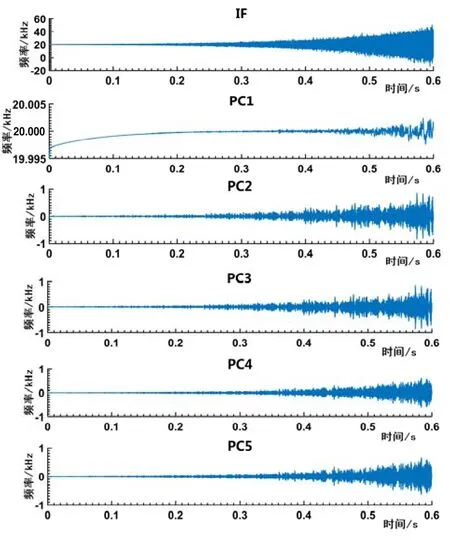
图3 瞬时频率IF及其PC1～PC5重构信号（SNR=50）Fig.3 Instantaneous frequency IF and the reconstructed signals corresponding to PC1～PC5 (SNR=50)

对比图2、图4可以看出，对于理想信号，本文方法同样可以准确地获得系统的骨架曲线和阻尼曲线，估计出的频率响应曲线清晰、无波动。不同之处在于，当SNR较低时，瞬时频率的估计值不再出现明显的波动，因此计算得到的骨架曲线仍然清晰易辨且没有出现明显的偏离，与理论曲线保持了很好的一致性，因此可以用来表征系统的非线性特性。相比之下，随着SNR的降低，阻尼曲线底部形状受噪声影响而变得更粗，但整个曲线保持了铅垂形状，与线性阻尼的假设相符。FRF曲线的情况与此类似，随着SNR的降低，FRF曲线的清晰程度呈现逐渐变差的趋势，但仍能清晰地反映出系统的频响特性。

2 实验与结果讨论

实验选用的测试对象为本实验室研制的一种环型振动微机械陀螺[22]。如图5所示，环型振动微机械陀螺包含两个环向相差45°的 2节点弯曲振动模态，并通过两个模态之间的科氏力耦合实现角速率的测量。该陀螺采用静电激励、电容检测方案，敏感结构采用金属管壳进行低气压封装以保证足够高的Q值。

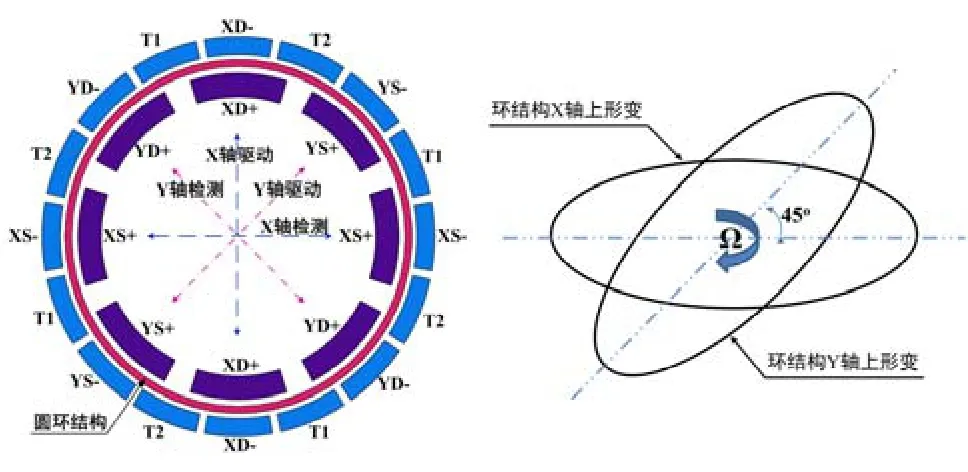
图5 实验选用的环形振动微机械陀螺Fig.5 Vibrating ring gyroscope under test

将Tektronix函数发生器AFG 3022B输出端与陀螺的驱动电极连接，在驱动轴(Y)方向驱动陀螺结构产生振动。检测轴(X)方向的位移响应信号通过连接于检测电极的电荷放大器获取。使用数据采集卡NI USB 6251，同步采集驱动轴激励信号和电荷放大器的输出响应信号。采集到的信号通过USB接口传输到计算机(PC)中，进行后续的信号处理与计算。

实验选用的微陀螺驱动轴固有频率约为24265Hz，激励信号为脉宽调制的正弦电压信号。为获得足够大的振幅，将激励频率fd设置为24265Hz，脉宽调制正弦信号的幅值选取为200mV。脉宽时间及自由衰减振荡观测时间分别确定为1.6 s、1.8s，以确保足以将陀螺激励至稳态振动，且可采集到足够长时段的共振衰减信号。采样频率fs设为250kHz（约10倍信号频率）。

实测的共振衰减信号以及由此计算得到的瞬时幅值、瞬时频率如图6所示。可以看出，由Hilbert变换计算得到的瞬时频率（图6(b)）呈现非常明显的波动。对其进行SSA处理，窗长L取为800。前5个主成分PC1～PC5的贡献率分别为94.214%、0.422%、0.420%、0.052%、0.052%。与图3结果类似，使用PC1重构得到的瞬时频率f(t)SSA如图6(c)所示。对比可知，经过SSA处理，噪声引起的非理想波动得到了明显的抑制。

对图 6(a)的瞬时幅值也进行类似处理，计算得到的骨架曲线、FRF曲线以及阻尼曲线如图7所示。由图可知，提取出的骨架曲线、FRF曲线清晰易辨，且随着振幅增大而呈现左侧弯曲的趋势，表明系统具有“软弹簧”的非线性特性。与之相比，阻尼系数则近似呈铅垂线变化，表明陀螺结构的阻尼基本呈现与振动幅值无关的线性特性。

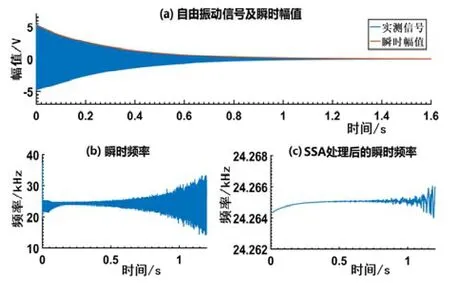
图6 实测信号及其瞬时幅值、瞬时频率Fig.6 The sampled signal and the corresponding instantaneous amplitude and instantaneous frequency

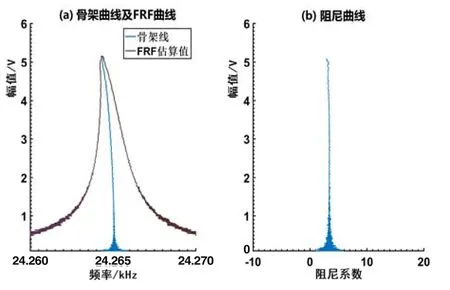
图7 实测信号的处理结果Fig.7 Processed curves of the sampled signal

为验证图7实验结果的可信度，采用频率扫描方式对该陀螺的幅频响应情况进行了测试。实验采用动态信号分析仪 HP35670A，正弦激励信号幅值选取80～175mV范围内的5个点，在24 257～24 269Hz范围内分别对陀螺进行频率扫描测量。频率步进量设为0.01Hz，时间间隔为1.5s。实测的频率响应曲线如图8所示。

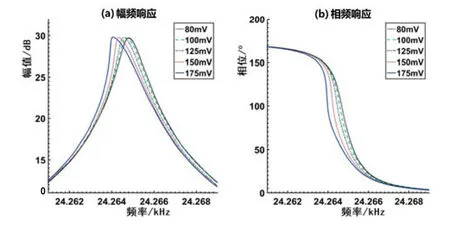
图8 扫频方法获得的频率响应曲线Fig.8 Frequency response curves obtained byfrequency sweeping

从图 8(a)中的幅频响应曲线中计算出响应信号的电压值，得到陀螺输出轴检测信号的电压-频率曲线如图9所示。可以看出，电压-频率曲线随着激励幅值增大，逐渐呈现“左偏”的趋势，反映出陀螺结构具有“软弹簧”特性。作为对比，图9中同时给出了图7(a)中的骨架曲线和FRF曲线。可以看出，采用本文方法所得到的骨架曲线、FRF曲线与频率扫描方式得到的结果在形状和变化趋势上均有较好的一致性。与频率扫描方式相比，本文方法所得到的测量结果整体向右偏移了约0.2 Hz。这主要是由于两种测量方式中陀螺的实际工作状态略有差异：频率扫描过程中陀螺工作于稳定激励-稳定响应状态，激励信号的驱动环节中除谐振器之外的其他因素也会反映到测量结果中。相比之下，共振衰减响应信号则直接来自谐振器的自由衰减振荡状态，在理论上，测量得到的结果更加准确地反映了谐振器自身的动力学特性。

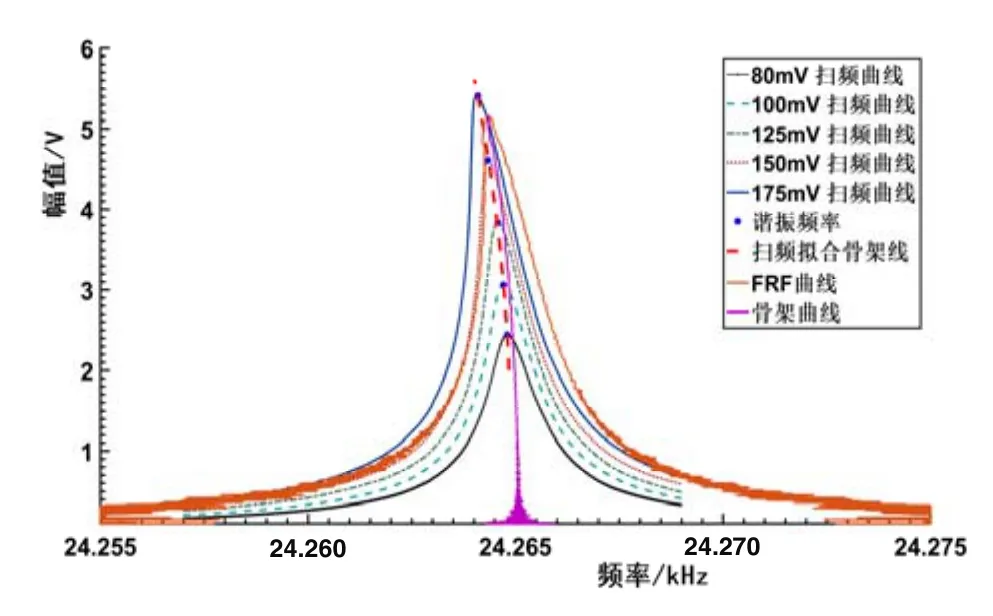
图9 骨架曲线、FRF曲线与扫频测量结果对比Fig.9 Comparison between the obtained Backbone curve,FRF curve and frequency sweeping measurement results

使用-3dB带宽法，对图8(a)中的幅频响应曲线进行处理，计算出Q值并换算得到微陀螺在不同振幅下的阻尼系数。图10为图7(b)阻尼系数曲线与扫频测量结果的对比情况。显然，两种分析结果具有良好的一致性，陀螺系统的阻尼系数基本上不受振幅增大的影响。

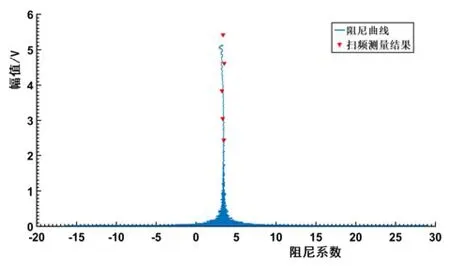
图10 图7(b)阻尼系数曲线与扫频测量结果对比Fig.10 Comparison between damping curve in Fig.7(b) and frequency-sweeping measurement results

3 结 论

研究了一种微机械陀螺非线性动力学特性的测量方法。采用Hilbert变换从共振衰减响应信号中提取出瞬时幅频参数，使用奇异谱分析处理得到瞬时幅值和瞬时频率的变化趋势，消除噪声引起的非理想波动。得到的骨架曲线、阻尼曲线及幅频曲线等特征信息清晰易辨，可用于系统非线性特性的分析和评估。不同信噪比下的仿真实验结果表明，这种方法的抗噪性能比FREEVIB法更好。针对MEMS环陀螺的实验测试结果与扫频法得到的测量结果具有良好的一致性，验证了这种方法在实际测试工作中的可用性。单次测量即可得到类似多次扫频的结果，是这种方法的突出优点。由于这种方法所测试的是微谐振器结构的动力学特性，因此对于其它种类微机械谐振器件的动力学特性测试而言，也具有很好的实用价值。

（References）：

[1]Tatar E, Mukherjee T, Fedder G K. Nonlinearity tuning and its effects on the performance of a MEMS gyroscope[C]//The 18thInternational Conference on Solid-State Sensors, Actuators and Microsystems (Transducers 2015). Alaska, USA, 2015: 1133-1136.

[2]Villanueva L G, Karabalin R B, Matheny M H, et al.Nonlinearity in nanomechanical cantilevers[J]. Physical Review B, 2013, 87(2): 024304.

[3]Mestrom R M C, Fey R H B, Phan K L, et al. Simulations and experiments of hardening and softening resonances in a clamped-clamped beam MEMS resonator[J]. Sensors and Actuators A: Physical, 2010, 162(2): 225-234.

[4]Mestrom R M C, Fey R H B, Van Beek J T M, et al.Modelling the dynamics of a MEMS resonator: simulations and experiments[J]. Sensors and Actuators A: Physical, 2008, 142(1): 306-315.

[5]Nitzan S H, Zega V, Li M, et al. Self-induced parametric amplification arising from nonlinear elastic coupling in a micromechanical resonating disk gyroscope[J]. Scientific Reports, 2015(5): 1-6.

[6]Hamed Y S, El-Sayed A T, El-Zahar E R. On controlling the vibrations and energy transfer in MEMS gyroscope system with simultaneous resonance[J]. Nonlinear Dynamics, 2016: 1-18.

[7]Ruzziconi L, Ramini A H, Younis M I, et al. Theoretical prediction of experimental jump and pull-in dynamics in a MEMS sensor[J]. Sensors, 2014, 14(9): 17089-17111.

[8]Wang C C, Yau H T. Nonlinear dynamic analysis and sliding mode control for a gyroscope system[J]. Nonlinear Dynamics, 2011, 66(1): 53-65.

[9]陈志勇, 周斌, 张嵘. 微机械角振动谐振器在低气压下的非线性振动[J]. 仪器仪表学报, 2010, 31(11): 2481- 2487.Chen Zhi-yong, Zhou Bin, Zhang Rong. Nonlinear vibration of micromachined angular vibration resonator in low pressure[J]. Chinese Journal of Scientific Instrument,2010, 31(11): 2481-2487.

[10]Sracic M W, Allen M S, Sumali H. Identifying the modal properties of nonlinear structures using measured free response time histories from a scanning laser Doppler vibrometer[M]. Topics in Nonlinear Dynamics. Springer New York, 2012, Vol. 3: 269-286.

[11]Feldman M. Nonparametric identification of asymmetric nonlinear vibration systems with the Hilbert transform[J].Journal of Sound & Vibration, 2012, 331(14): 3386-3396.

[12]Feldman M. Hilbert transform methods for nonparametric identification of nonlinear time varying vibration systems[J]. Mechanical Systems & Signal Processing, 2014,47(1-2): 66-77.

[13]Feldman M. Hilbert transform applications in mechanical vibration[M]. John Wiley & Sons, 2011.

[14]Yang Y, Peng Z K, Dong X J, et al. Nonlinear timevarying vibration system identification using parametric time–frequency transform with spline kernel[J]. Nonlinear Dynamics, 2016: 1-16.

[15]Peng Z K, Meng G, Chu F L, et al. Polynomial chirplet transform with application to instantaneous frequency estimation[J]. IEEE Transactions on Instrumentation &Measurement, 2011, 60(9): 3222-3229.

[16]Wang C, Ren W X, Wang Z C, et al. Instantaneous frequency identification of time-varying structures by continuous wavelet transform[J]. Engineering Structures,2013, 52(9): 17-25.

[17]İçer S, Ş Gengeç. Classification and analysis of nonstationary characteristics of crackle and rhonchus lung adventitious sounds[J]. Digital Signal Processing, 2014,28(4): 18-27.

[18]Walwer D, Calais E, Ghil M. Data-adaptive detection of transient deformation in geodetic networks[J]. Journal of Geophysical Research Solid Earth, 2016, 121(3): 2129- 2152.

[19]Ghanati R, Kazemhafizi M, Mahmoudvand R, et al.Filtering and parameter estimation of surface-NMR data using singular spectrum analysis[J]. Journal of Applied Geophysics, 2016, 130: 118-130.

[20]Luo S, Cheng J, Zeng M, et al. An intelligent fault diagnosis model for rotating machinery based on multi-scale higher order singular spectrum analysis and GA-VPMCD[J].Measurement, 2016, 87: 38-50.

[21]Feldman M, Bucher I, Rotberg J. Experimental identification of nonlinearities under free and forced vibration using the Hilbert transform[J]. Journal of Vibration &Control, 2009, 15(10): 1563-1579.

[22]李昊. 多环结构微机械陀螺研究[D]. 北京: 清华大学,2015: 46-108.Li Hao. Research on muti-ring structure micromachined gyroscopes[D]. Beijing: Tsinghua University, 2015: 46-108.

[23]卓宁, 张海江, 张小虎. 基于希尔伯特－黄变换的去噪法在外测数据处理中的应用[J]. 中国惯性技术学报,2015, 23(1): 137-140.Zhuo Ning, Zhang Hai-jiang, Zhang Xiao-hu. Application of Hilbert-Huang transform-based de-noising method in processing exterior ballistic measurement data[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 137-140.

Extraction of micromechanical gyroscope’s backbone curves from resonance decay responses

WEI Yu-miao1,2, DONG Yong-gui1
(1. State Key Laboratory of Precision Measurement Technology and Instruments, Dept. of Precision Instrument, Tsinghua University, Beijing 100084, China; 2. Unit 202, Rocket Force University of Engineering, Xi’an 710025, China)

In order to measure the nonlinear characteristics of MEMS gyroscopes, a method for extracting Backbone curves from the resonance decay responses is investigated. By using Hilbert transform to process the resonance decay signals, the singular spectrum analysis on the calculated instantaneous amplitudes and instantaneous frequencies is carried out to remove the non-ideal fluctuations caused by the noises, and the concentrated and legible Backbone curves are obtained. In such a way, the noise sensitive problems in Hilbert transform-based identification methods are suppressed. Numerical simulation for a Duffing system show that the proposed method exhibits better anti-noise performance than FREEVIB. A vibrating ring micro gyroscope is experimentally tested. The obtained backbones curves, damping curves and frequency-response curves all coincide with those obtained by traditional frequency sweeping method.As a general measurement technique, the proposed method is also applicable to test the dynamic features of other kinds of micromechanical resonators.

MEMS gyroscopes; nonlinear features; Hilbert transform; backbone curve; singular spectrum analysis

V241.5；TN911.7

A

1005-6734(2016)05-0660-06

10.13695/j.cnki.12-1222/o3.2016.05.018

2016-07-30；

2016-09-28

国家自然科学基金资助项目（61271129）

魏玉淼（1988—），男，博士研究生，从事微机电传感器系统测试研究。E-mail: 824035931@qq.com

联 系 人：董永贵（1965—），男，教授，博士生导师。E-mail: dongyg@mail.tsinghua.edu.cn