惯性测量系统火箭橇试验振动传递特性

魏宗康，黄云龙

（北京航天控制仪器研究所，北京 100854）

惯性测量系统火箭橇试验振动传递特性

魏宗康，黄云龙

（北京航天控制仪器研究所，北京 100854）

惯性测量系统火箭橇试验过程中，惯性测量系统根据试验要求安装于减振平板上，而减振平板通过金属减振器安装于橇体上。通过振动传感器实时测量和记录橇体、减振平板和惯性测量系统的振动和冲击信号，待试验结束后读取记录存储的数据并进行振动量级、振动传递和减振效果分析。提出了一种描述惯性测量系统火箭橇试验振动传递特性的方法，包括振动谱图例对比、振动谱比值对比和基于AR模型幅值修正的传递函数描述方法。通过对各部分数据进行比较，验证了数据处理方法的正确以及描述惯性测量系统火箭橇试验振动传递特性的有效性。

惯性测量系统；火箭橇试验；振动传递特性；AR模型

火箭橇试验是唯一可以实现较长时间的大过载高动态试验，其集成了过载、振动、冲击等单项试验条件[1-6]，利用火箭橇试验验证惯性测量装置的功能和精度具有非常重要的意义。由于火箭橇试验时，振动量级和运行速度直接相关，速度越大会引起振动幅值也增大，为减小随机振动对惯性测量系统的影响[7-8]，除产品自身减振器外，还增加金属减振平板以起到隔振的功能，如图1所示。

图1 惯性测量系统在减振平板上的安装示意图Fig.1 IMU fixed on vibration damper plate

试验时，惯性测量系统采取减振措施固定在减振平板上，减振平板再通过4个金属隔振器安装于橇舱内，因此要对减振平板的隔振功能进行验证以达到惯性测量系统所要求的力学环境。从振动传递顺序来看，橇体振动传递到减振平板，减振平板的振动传递到被试产品。因此，需要研究在传递过程中，振动量级是否增大或衰减，且在不同的频段其传递特性是否相同[9-11]。本文具体研究了惯性测量系统火箭橇试验时的振动传递特性的描述方法。

1 火箭橇试验振动测试系统组成

振动测试系统由传感器、数据采集记录系统、触发装置和信号传输电缆等组成。测试系统中传感器、数据采集系统和触发装置通过信号传输电缆连接，各部件在橇体上的安装可采用压条、螺栓紧固的方式，具体包括：

1）在橇体、减振平板和惯性测量系统壳体上分别安装不少于3个输入轴正交的传感器，分别测量安装位置处的航向加速度、竖向加速度和侧向加速度；

2）数据采集系统、触发装置直接安装于橇体上；

3）信号传输电缆根据布线方式采用捆扎成束就近与橇体固连。

测试系统在火箭橇试验时的工作过程包括：

1）数据采集记录系统在一个采样周期内完成对安装于橇体上三向（航向、竖向和侧向）传感器、减振平板上三向（航向、竖向和侧向）传感器、惯性测量系统壳体上三向（航向、竖向和侧向）传感器等信号的采集和记录，见图2；

2）在火箭橇发射前，对测试系统复位，使其处于待触发（记录）状态；

3）在工作前至少5 s，测试系统开始工作并记录数据；

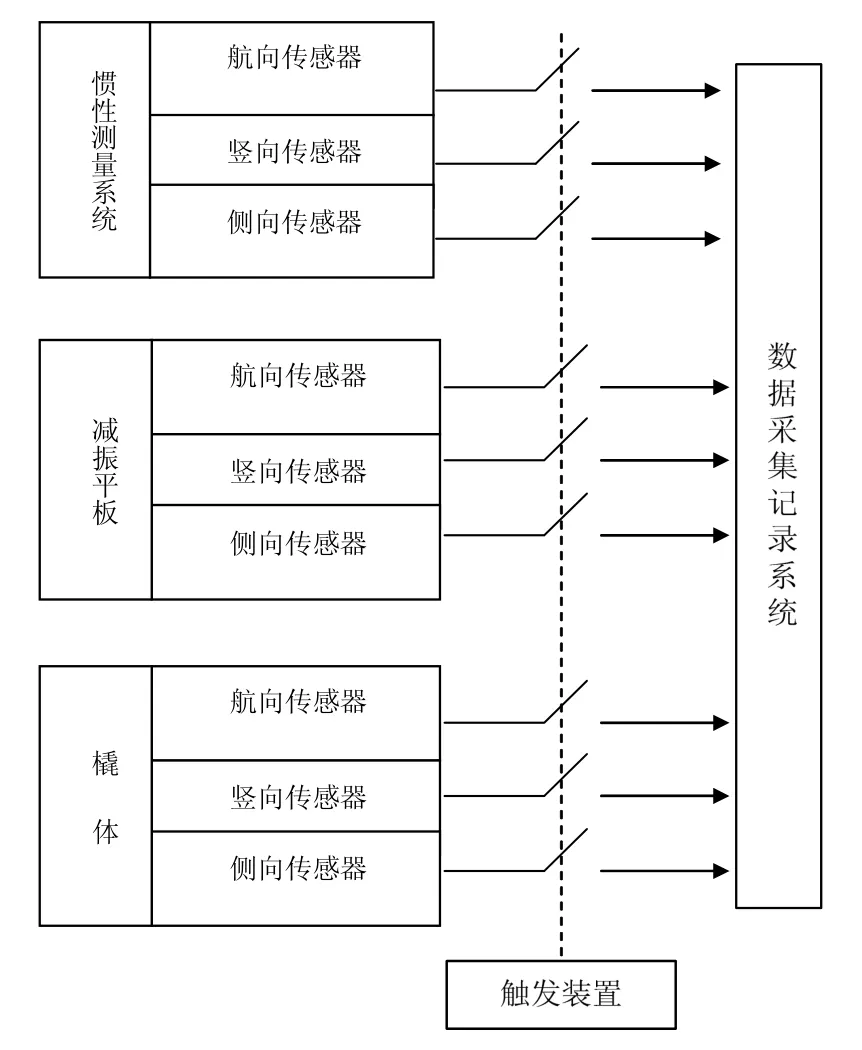
图2 振动传感器信号的采集和记录Fig.2 Signal acquisition and recording of vibration sensor

4）在橇体运行结束后，测试系统根据预先设置的时刻停止采集与记录；

5）火箭橇试验后，读取、检查并确认记录数据完整、正确。

2 振动数据谱分析

惯性测量系统火箭橇试验各通道振动数据基于周期谱的的特征统计参数包括线谱、功率谱密度等。采用正频域的计算方法如下：

信号ad(k)经过傅立叶变换后可求得线谱序列ck。采用正频域的频谱时，频率计算公式如式(1)所示，线谱的计算公式如式(2)所示，功率谱密度的计算公式如式(3)所示。

式中：ck为基于正频域计算的线谱序列(g0)；ad(n)为计算的振动序列(g0)；fk为频率(Hz)；N为数据的时间长度(s)；T为数据的时间长度(s)；F(k)为离散傅立叶变换；Φ(fk)为计算的在频率fk处的功率谱密度（g02/Hz）。

3 火箭橇试验振动传递谱计算方法

目前，在数据处理过程中，只是定性分析各级的振动量级大小、有无谐振峰值等，缺少对橇体至减振平台、减振平台至被试产品、橇体至被试产品的振动传递特性进行分析。因此，需要研究一种方法来判断被试产品在火箭橇试验时的振动传递量级。在描述惯性测量系统火箭橇试验时振动的传递特性时，可采用振动谱图例对比和振动谱比值对比等两种方法。

3.1 振动谱图例对比

振动谱图例对比是分别对航向、竖向和侧向的振动功率谱密度进行对比，具体包括：

1）把橇体、减振平板和惯性测量系统的航向振动功率谱密度数据绘制于倍频示意图中，直接根据其相对大小定性确定航向的振动传递特性；

2）把橇体、减振平板和惯性测量系统的竖向振动功率谱密度数据绘制于倍频示意图中，直接根据其相对大小定性确定竖向的振动传递特性；

3）振平板和惯性测量系统的侧向振动功率谱密度数据绘制于倍频示意图中，直接根据其相对大小定性确定侧向的振动传递特性。

平台系统火箭橇试验时，采用振动谱图例对比法。橇体、减振平板和产品的航向振动功率谱密度如图3所示，竖向振动功率谱密度如图4所示，侧向振动功率谱密度如图5所示。图3～5中，红色曲线为橇体的振动功率谱密度，蓝色曲线为减振平板的振动功率谱密度，黑色曲线为产品的振动功率谱密度。

图3 火箭橇试验中的橇体、减振平板和产品的航向振动功率谱密度Fig.3 Azimuth vibration PSD of the sled, the vibration damper plate and the product

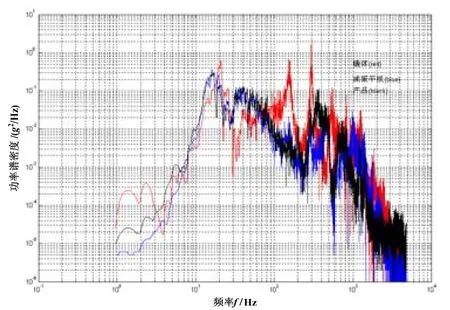
图4 火箭橇试验中的橇体、减振平板和产品的竖向振动功率谱密度，Fig.4 Vertical vibration PSD of the sled, the vibration damper plate and the product

图5 火箭橇试验中的橇体、减振平板和产品的侧向振动功率谱密度Fig.5 Side direction vibration PSD of the sled, the vibration damper plate and the product

3.2 振动谱比值对比

在描述2个振动传感器测量的振动传递谱时，计算步骤主要包括以下三个步骤：

1）通过安装于振源的传感器高速采样测量出橇体运行时的振动计算值序列adx(k)，k=1,2,…,N；同时，通过另一个高速采样的传感器测量出被试品运行时的振动计算值序列ady(k)，k=1,2,…,N；

2）根据式(1)～(3)计算振动数据adx(k)和ady(k)的基于周期谱的功率谱密度Φx(fk)、Φy(fk)，k=1,2,…,N/2；

3）计算振动传递谱：

但由于火箭橇试验时采用多级传感器，振动谱比值对比是分别对航向、竖向和侧向的振动功率谱密度进行量化对比，具体包括：

1）把航向/竖向/侧向的减振平板振动谱密度数据与橇体振动谱密度数据相比，将其比值作为橇体至减振平板的振动传递量化数据，并绘制于倍频示意图中；

2）把航向/竖向/侧向的惯性测量系统振动谱密度数据与减振平板振动谱密度数据相比，将其比值作为减振平板至惯性测量系统的振动传递量化数据，并绘制于倍频示意图中；

3）把航向/竖向/侧向的惯性测量系统振动谱密度数据与橇体振动谱密度数据相比，将其比值作为惯性测量系统至惯性测量系统的振动传递量化数据，并绘制于倍频示意图中。

平台系统火箭橇试验时，采用振动谱比值对比法。橇体、减振平板和产品之间的航向振动传递功率谱密度曲线如图6所示。可以看出：减振平板相对橇体在500 Hz以上的振动谱比值小于 1，表明其振动幅值得到衰减；但在10～150 Hz的振动谱比值大于1，表明其振动得到放大。而平台相对减振平板的振动传递比值都大于1，意味着平台相对于减振平板的振动得到放大。

图6 橇体、减振平板和产品之间的航向振动传递功率谱密度曲线Fig.6 Azimuth vibration delivery PSD among the sled, the vibration damper plate and the product

4 基于参数模型的振动传递函数

采用振动传递谱进行分析时，只对各级振动信息开展了周期功率谱分析，其特点是噪声大，缺少有效的降噪处理方法。在分析火箭橇试验时的振动传递规律时，为克服噪声，在火箭橇试验中拟采用AR模型谱估计，其具备一些好的性质，最主要的是平滑特性[12-13]，这是因为AR模型是一个有理分式。另外，在阶次较高时，各频率点的波峰和波谷也较为准确。但其缺点是整体幅值受随机信号是否平稳等因素影响而相对真实值有偏离。综上所述，需要研究一种描述被试产品在火箭橇试验时的振动传递量级和传递函数的方法。

4.1 振动功率谱传递函数计算方法

本文提出了一种火箭橇试验振动功率谱传递函数计算方法，其计算步骤如下：

1）通过安装于橇体的传感器高速采样并经高通滤波，测量出橇体运行时的振动计算值序列 adx(k)，k=1,2,…,N；同时，通过另一个高速采样的传感器高速采样并经高通滤波，测量出被试品运行时的振动计算值序列 ady(k)，k=1,2,…,N；

2）根据公式(1)～(3)，计算基于周期谱的特征统计参数包括线谱ckx(fk)、cky(fk) (k=1,2,…,N/2)以及功率谱密度Φx(fk)、Φy(fk) (k=1,2,…,N/2)；

3）计算步骤 1）振动数据 adx(k)和 ady(k)的基于AR参数模型功率谱传递函数Px(fk)、Py(fk)；

4）修正步骤 3）中功率谱传递函数 Px(fk)、Py(fk)的幅值大小，得到 P′x(fk)、P′y(fk)；

5）利用步骤 4）计算的功率谱密度 P′x(fk)、P′y(fk)，计算振动功率谱传递谱函数：

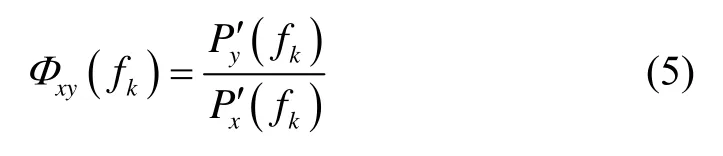
4.2 AR参数模型功率谱传递函数计算方法

在4.1节步骤3）中基于AR参数模型功率谱传递函数Px(fk)、Py(fk)计算过程为：

1）设橇体振动的数据序列adx(k)的自相关序列rx(i)，i=0,1,…,N-1；被试品振动的数据序列ady(k)的自相关序列ry(i)，i=0,1,…,N-1。二者的计算表达为

2）计算自相关序列，可分别求出 AR模型的各项系数。具体计算公式为

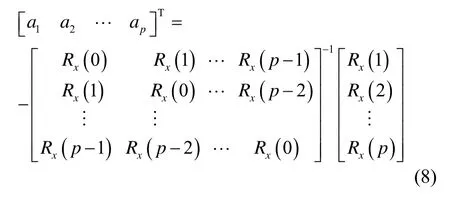
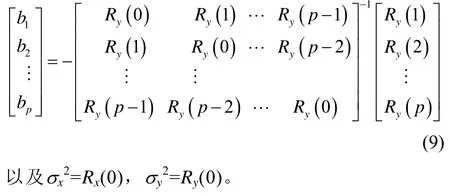
3）设橇体振动的数据序列adx(k)描述为一个受方差为1的白噪声序列u1(n)激励后的结果，其AR模型和功率谱的表达为

式中：p为橇体振动AR模型的阶次；Hx(z)为橇体振动AR模型；Px(fk)为橇体振动功率谱；a0、a2、…、ap、σx为橇体振动AR模型的参数。

4）设被试品振动的数据序列ady(k)描述为一个受方差为 1的白噪声序列 u2(n)激励后的结果，其AR模型和功率谱的表达为

式中：p为被试品振动AR模型的阶次；Hy(z)为被试品振动 AR模型；Py(fk)为被试品振动功率谱；b0、b2、…、bp、σy为被试品振动AR模型的参数。

4.3 振动功率谱传递函数幅值修正方法

在4.1节步骤4）中的修正功率谱传递函数Px(fk)、Py(fk)的幅值大小的计算过程为：

1）由功率谱Φx(fk)、Φy(fk)以及功率谱 Px(fk)、Py(fk)，计算得到幅值的比例系数cx、cy。具体计算公式为

2）由比例系数 cx、cy以及功率谱Px(fk)、Py(fk)，计算得到 P′x(fk)、P′y(fk)。具体计算公式为

5 试验数据对比

下面给出采用周期谱的功率谱与采用AR模型的功率谱的数据处理结果。

5.1 单通道振动功率谱密度对比

图7给出了橇体航向振动基于AR模型和基于周期谱的功率谱密度，图8给出了减振平台振动基于AR模型和基于周期谱的功率谱密度，图9给出了被试产品（惯性平台系统）振动基于AR模型和基于周期谱的功率谱密度。图7～9中，红色曲线为基于AR模型的功率谱密度，黑色曲线为基于周期谱的功率谱密度。从图中可以看出，基于周期谱的功率谱密度曲线噪声较大，而基于AR模型的功率谱密度曲线相对平滑。

图7 橇体航向振动基于AR模型与基于周期谱的功率谱密度Fig.7 Azimuth vibration PSD of the vibration damper plate based on AR model vs. periodic spectrum

图8 减振平板航向振动基于AR模型与基于周期谱的功率谱密度Fig.8 Azimuth vibration PSD of the sled based on AR model vs. periodic spectrum

图9 被试产品航向振动基于AR模型与基于周期谱的功率谱密度Fig.9 Azimuth vibration PSD of the product based on AR model vs. periodic spectrum

5.2 振动功率谱密度传递函数对比

基于AR模型的橇体、减振平板和产品之间的航向振动传递功率谱密度曲线如图10所示，具体包括：

1）把航向的减振平板基于AR模型的振动谱密度数据与橇体振动基于 AR模型的谱密度数据相比后的传递函数幅值；

2）把航向的惯性测量系统振动基于AR模型的谱密度数据与减振平板振动基于AR模型的谱密度数据相比后的传递函数幅值；

3）把航向的惯性测量系统振动基于AR模型的谱密度数据与橇体振动基于AR模型的谱密度数据相比后的传递函数幅值。

与图6结果对比可以看出，采用修正后的基于AR模型的功率谱密度与基于周期谱的功率谱密度基本重合，但其具有可连续平滑的优势。

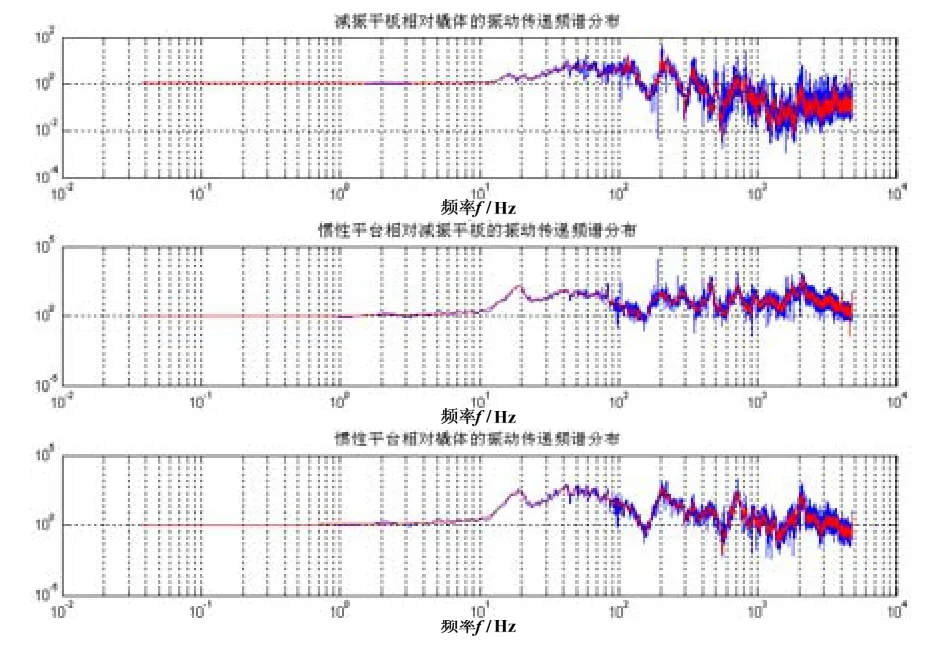
图10 橇体、减振平板和产品之间的航向振动传递功率谱密度曲线Fig.10 Azimuth vibration delivery PSD among the sled, the vibration damper plate and the product

6 结 论

本文针对火箭橇试验中的三维振动数据特点，分别给出不同的振动传递特性描述和处理方法，包括振动谱图例对比、振动谱比值对比和基于AR模型幅值修正的传递函数描述方法。通过对各部分数据进行比较，验证了数据处理方法的正确以及描述惯性测量系统火箭橇试验振动传递特性的有效性。总之，本文提出的方法对惯性测量系统进一步开展火箭橇试验时减振方案设计及其优化奠定了良好的基础。

（References）：

[1]Zhang Jian-hua, Jiang Shou-shan. Definition of boundary conditions and dynamic analysis of rocket sled and turntable[J]. Advances in Mechanical Engineering, 2011,52(54): 261-266.

[2]Zhang Jian-hua, Jiang Shou-shan. Rigid-flexible coupling model and dynamic analysis of rocket sled[J]. Advance Materials Research, 2012, 346: 477-454.

[3]刘璠, 魏宗康, 刘建波, 等. 一种惯性测量装置火箭橇试验误差分离方法[J]. 中国惯性技术学报, 2014, 22(1):131-134.Liu Fan, Wei Zong-kang, Liu Jian-bo, et al. Error separation based on rocket sled test of inertial measurement device[J]. Journal of Chinese Inertial Technology, 2014,22(1): 131-134.

[4]段宇鹏, 魏宗康, 刘建波, 等. 惯性测量装置火箭橇试验外测数据融合方法[J]. 中国惯性技术学报, 2013,21(4): 553-556.Duan Yu-peng, Wei Zong-kang, Liu Jian-bo, et al. Data fusion method based on rocket sled test of inertial measurement device[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 553-556.

[5]段宇鹏, 魏宗康, 刘建波. 一种 GPS最优选星及伪距定位方法[J]. 中国惯性技术学报, 2013, 21(2): 209-213.Duan Yu-peng, Wei Zong-kang, Liu Jian-bo, et al. Optimal satellite selection and pseudo range positioning of GPS[J].Journal of Chinese Inertial Technology, 2013, 21(2): 209-213.

[6]刘建波, 魏宗康, 景建斌, 等. 惯性测量装置火箭橇试验过载曲线设计方法[J]. 中国惯性技术学报, 2012,20(1): 117-121.Liu Jian-bo, Wei Zong-kang, Jing Jian-bin, et al. Overload curve design based on rocket sled test of inertial measurement device[J]. Journal of Chinese Inertial Technology, 2012, 20(1): 117-121.

[7]Song Ning-fang, Cai Qing-zhong, Yang Gong-liu, et al.Analysis and calibration of the mounting errors between inertial measurement unit and turntable in dual-axis rotational inertial navigation system[J]. Measurement Science & Technology, 2013, 24(11): 1933-1951.

[8]刘建波, 魏宗康. 石英加速度计误差系数显著性分析[J]. 中国惯性技术学报, 2011, 19(5): 615-620.Liu Jian-bo, Wei Zong-kang. Error coefficients’ significant analysis of quartz accelerometer[J]. Journal of Chinese Inertial Technology, 2011, 19(5): 615-620.

[9]Rahmatalla S, Hudson K, Ye Liu, et al. Finite element modal analysis and vibration-waveforms in health inspection of old bridges[J]. Finite Elements in Analysis &Design, 2014, 78(1): 40-46.

[10]Zhu Xiao-hua, Liu Yun-hai, Tong Hua, et al. Analysis of reamer failure based on vibration analysis of the rock breaking in horizontal directional drilling[J]. Engineering Failure Analysis, 2014, 37(37): 64-74.

[11]Ghasemloonia A, Rideout D G, Butt S D, et al.Vibration analysis of a drillstring in vibration-assisted rotary drilling: finite element modeling with analytical validation[J]. Journal of Energy Resources Technology,2013, 135(3): 364-392.

[12]Cong Fei-yun, Chen Jin, Guan-ming Dong, et al. Spectral kurtosis based on AR model for fault diagnosis and condition monitoring of rolling bearing[J]. Journal of Mechanical Science and Technology, 2012, 26(2): 301-306.

[13]Ye Liu, Huang Zhi-ping, Su Shao-jing, et al. AR model whitening and signal detection based on GLD algorithm in the non-Gaussian reverberation[J]. Applied Acoustics,2012, 73(10): 1045-1051.

Vibration delivery characteristics based on rocket sled testing of inertial measurement system

WEI Zong-kang, HUANG Yun-long
(Beijing Institute of Aerospace Control Devices, Beijing 100854, China)

In the rocket sled test for an inertial measurement system, the inertial measurement system should be installed onto a vibration damper plate, which is fixed on the sled via metal dampers, according to related testing requirements. The vibration and pulse signals of the sled as well as the vibration damper plate and the inertial measurement system are measured and recorded in real time by vibration sensors. After the sled testing, the recorded data are read out, and then its vibration order, vibration delivery and damping effect are analyzed. A new method for describing the vibration delivery characteristics of inertial measurement system rocket sled testing is put forward, which includes the diagram comparison of vibration spectrums, the specific value comparison of vibration spectrums as well as the transfer function description based on AR model magnitude modification. Data comparison from related aspects verifies that the correctness of data processing method is and the effectiveness of the describing method for the vibration delivery characteristics in rocket sled testing of inertial measurement system.

inertial measurement system; rocket sled test; vibration delivery characteristics; AR model

U666.1

A

1005-6734(2016)05-0666-06

10.13695/j.cnki.12-1222/o3.2016.05.019

2016-07-25；

2016-09-29

国防基础科研项目（B0320080021）；民用航天专业技术预先研究项目（D010101）

魏宗康（1973—），男，研究员，从事导航、制导与控制专业研究。 E-mail: weizongs@yahoo.cn