基于最优PID和LQG算法的空间望远镜大口径快摆机构控制系统仿真

张茜丹，魏传新，尹达一

（1. 中国科学院大学，北京 100039；2. 中国科学院上海技术物理研究所，上海 200083）

基于最优PID和LQG算法的空间望远镜大口径快摆机构控制系统仿真

张茜丹1,2，魏传新1,2，尹达一1,2

（1. 中国科学院大学，北京 100039；2. 中国科学院上海技术物理研究所，上海 200083）

空间望远镜在观测时会受到不确定性扰动，这些扰动的特性为幅值小，频带宽，控制难，而且望远镜平台的振动成分大部分在10 Hz以内。为了减小这些低频振动造成的干扰，对空间望远镜的大口径FSM系统进行控制器设计使其能够对低频扰动具有良好的抑制作用，选择的控制算法为在ITAE指标最优情况下的PID算法和带有积分作用的LQG算法。利用Simulink对系统搭建模型，仿真结果表明：FSM系统在PID控制器作用下的响应时间为0.4 s, 在LQG控制器作用的响应时间为0.04 s，且都无稳态误差。利用OICETS卫星的振动功率谱密度数据对系统的抑制能力进行验证，在低频段0～10 Hz范围内：跟踪模式时，系统在PID控制器作用下，抑制能力为14.5 dB，系统在LQG控制器作用下，抑制能力为32.5 dB；瞄准模式时，系统在PID控制器作用下，抑制能力为10.3 dB，系统在LQG控制器作用下，抑制能力为23.6 dB。经过比较，该大口径FSM系统在LQG控制器作用下的系统性能明显优于在最优PID控制器作用下。

大口径快摆机构控制系统；扰动抑制；PID算法；LQG算法

在空间进行天文观测可以摆脱大气影响，具有较低的背景噪声而且观测波长范围广，望远镜的角分辨率接近衍射极限，所以空间天文望远镜已成为天文观测的重要手段。空间望远镜口径越大，聚光能力越强，分辨率越高，所以大口径空间望远镜可以获得更清晰的图像和更全面的信息。空间望远镜在轨运行时工作环境复杂，受到多种微振动影响，不同频率和振幅的振动会对像质产生不同的影响[1]。为了实现空间望远镜预期的探测精度，保证系统的分辨率不下降，图像性能不退化，这就要求空间望远镜具有极高的稳像能力。

目前国内尚无在轨运行的大口径空间望远镜，为了实现空间望远镜的大视场观测，系统可以在观测目标光源与接收探测器之间通过控制大口径快速摆动镜（Fast Steering Mirror，FSM），在一定摆角范围内以一定速度调整光轴的稳定，实现光学系统的高速精确指向、跟踪和图像稳定。由于FSM具有大口径，大惯量，如果要想取得高的定位精度和良好的动态性能，无论是采用开环控制还是闭环控制，都需要与一定的控制算法相结合。通过对快摆镜结构的频响特性进行测量与分析，建立数学模型，采用可靠的控制算法，可提高系统的跟踪和响应能力。

1 空间望远镜平台扰动分析

在FSM系统设计初期，首先要分析扰动的来源以及特性[2]。空间望远镜受到的扰动来源分别是航天器所处空间环境带来的扰动，外部扰动源和内部扰动源。外部扰动源主要是望远镜平台振颤带来的扰动，内部扰动源主要与望远镜自身进行的某些特定操作有关。其中部分扰动来源如表1所示。望远镜平台振颤是FSM系统最大扰动源，所以了解望远镜平台振动频谱特性对于稳像系统而言是必要的。

对于特定的望远镜平台，在设计初期很难给出其本身的振动数据，所以需要参考已经成功发射的卫星振动数据，根据这些经验数据开展系统仿真估计。

Sudey和Sculman在1984年发表了由美国航空航天局（NASA）发射的LANDSAT-4卫星振动功率谱密度（Power spectral density，PSD）数据[3]。Wittig在1990年发表了由欧洲航天局（ESA）发射的OLYMPUS通信卫星PSD数据[4]。欧洲航天局SILEX计划采用式(1)作为卫星平台振动 PSD 函数[4]，为图 1中的ESAspec曲线。首先根据式(1)在实验室对 ARTEMIS飞船进行了振动测试[5]，卫星发射后，对ETS-VI卫星做了在轨测量[6]，测量数据为图1中ETS-VI曲线。

表1 望远镜平台扰动来源Tab.1 Disturbance source of telescope platform

日本科学家先在实验室对OICETS通信卫星的振动情况做了最坏的预测[7]，并在卫星发射之后对其振动情况做了测试。对比实验室与在轨数据发现，卫星在轨的振动程度比在实验室预测的更严重[8]。图1所示为典型的卫星平台振动功率谱密度[9]。LANDSAT和OLYMPUS使用相同的加速度计测量，LANDSAT的振动频率最高达128 Hz，OLYMPUS卫星的振动频率最高达500 Hz。ETS_VI的振动数据是由位于其快摆镜上的角位移测量装置测得的，频率最高可达250 Hz。OICETS卫星由加速度计分别测试了跟踪和瞄准模式下1 Hz到1024 Hz的振动数据。

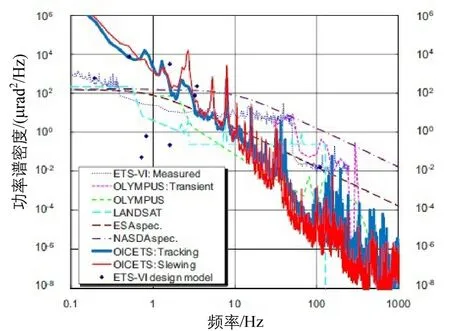
图1 典型的卫星平台振动功率谱密度Fig.1 Vibration power spectrum density of typical satellite platform

空间飞行器与有效载荷交界处的振动均方根值可以由式(2)计算得到：

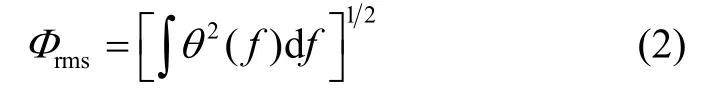
对OICETS卫星振动数据进行计算，在表2中可以看到振动在每个频率段的分布，大部分的振动成分都在10 Hz以下。由这些数据可以看出，振动显示出低频高幅，高频低幅的特性。通常情况下低频振动包括太阳电池阵列由于共振或热瞬态影响引起的偏转及偏航机动等，这类扰动频率较低，一般是几Hz量级。而高频振动一般振动幅度在微弧度量级，带宽 1～2 kHz，机械装置、电机和其他硬件都可以产生这类扰动。总的可以将空间卫星平台的振动概括为幅值小、频带宽、控制难。对于高频段（10 Hz以上）的振动，通常利用隔离系统进行隔离，这种被动隔振的方法对于高频振动有良好的隔振效果；对低频段（10 Hz以下）振动，在空间望远镜主光学系统后端与成像探测器之间设计精密稳像系统。其中精密稳像系统的主体为大口径FSM，通过驱动大口径FSM在特定摆角范围内的运动来消除振源对负载的扰动影响，可以高精度的补偿平台姿态变化、振颤等引起的星象模糊，最终实现望远镜光学系统的高速精确跟踪[10]、指向及成像稳定。

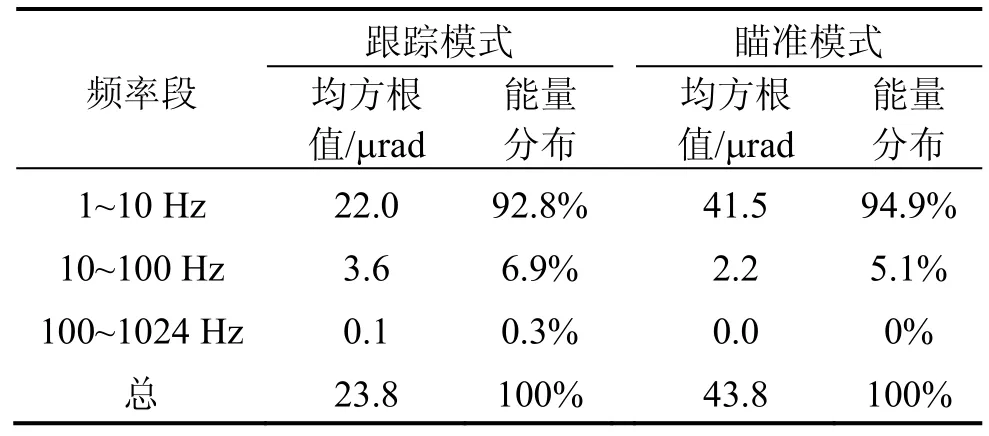
表2 振动频率分布情况Tab.2 Distribution of vibration frequency

2 大口径FSM系统分析

对于FSM系统设计控制器，系统所用的FSM主要由驱动器、支撑架和镜体三部分组成，镜体口径为600mm。选择输出带宽大、精度高的压电陶瓷制动器（PZT）作为系统的驱动机构[11]；选择柔性铰链来支撑镜面，具有精度更高，谐振频率更高，没有摩擦，无需润滑等优点[12]。FSM系统框图如图2所示。

FSM系统中，粗级控制系统的输入为期望视轴位置R，输出为YF，它们之间的控制残差为E。

图2 FSM系统原理图Fig.2 Schematic of motor system

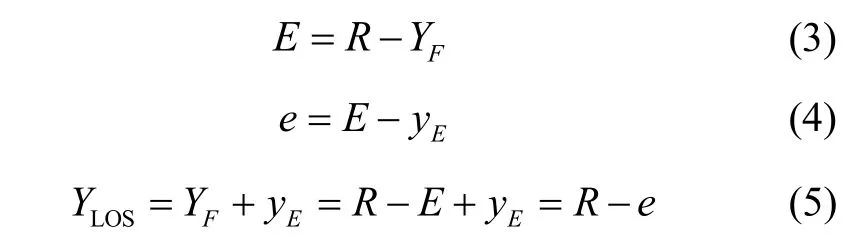
以粗级控制系统的残差E作为精级控制系统的输入，采用合适的控制算法对FSM进行控制，使其输出的补偿残差yE与粗级控制系统的残差E之间的差异e比E小得多。这样补偿残差yE与粗级控制系统的输出YF进行累加，可以得到与期望视轴位置R误差更小的视轴指向YLOS。由式(4)可知，FSM的补偿残差决定了视轴稳定精度。

通过对 FSM 系统进行系统辨识，输入是驱动器PZT的工作电压U，输出是FSM的转动角度θ。得到FSM绕一个轴平动时的状态方程[13]，如式(6)所示：

3 大口径FSM系统的控制器仿真

对于FSM系统控制器的设计，选择Matlab中控制工具箱与Simulink仿真系统相结合的方法，针对式(6)所示的FSM系统，设计适合的控制器，给出在控制器作用下的系统特性以及系统对扰动抑制的仿真结果。

3.1 最优PID控制器仿真

PID控制器在工业界应用最广泛[14]。将最优控制器设计与数值最优化问题结合起来，将Matlab语言的寻优能力与Simulink的系统仿真结合起来，可以解决PID控制器参数的确定问题。

连续PID控制器的典型形式为

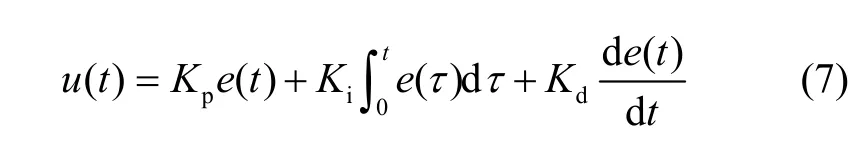
Laplace变换形式可以写成：

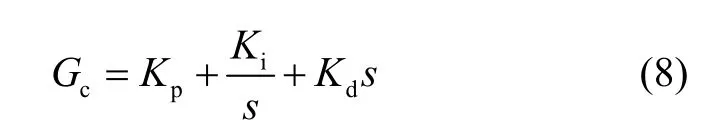
式中：KP、Ki和Kd分别是对系统误差信号e(t)及其积分、微分量的加权。在实际应用中，由于纯微分环节不能直接使用，通常用带有滤波作用的一阶环节来近似描述，所以设计的PID控制器的最终形式如式(9)所示：其中，Tf是滤波时间常数。

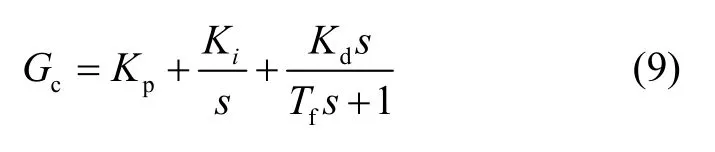
经过Simulink建立模型和Matlab寻优，得到在ITAE指标最优情况下的PID控制器。ITAE是一种最优化指标，其定义为

基于 ITAE指标的最优控制，可以实现控制系统的目标函数最小。通过对时间的加权方式使得无法控制的初始时刻的误差加权变小，使得系统能够保证调节时间变短，但调节的动态过程却会更稳定[15]。得到PID控制器为

系统在该PID控制器的作用下，闭环阶跃响应和开环频率响应如图3所示。

由PID控制系统的闭环阶跃响应图可以得到系统的响应时间为0.4 s，无稳态误差；由开环伯德图可以得到，系统幅值裕度为9.73 dB，相角裕度为89，系统稳定。

图3 在PID控制器作用下的系统特性Fig.3 System performance with PID controller

3.2 LQG控制器仿真

LQG是对已知的控制对象用式(12)表示：

dω和nω分别是扰动和量测噪声，通常假设它们为不相关的零均值白噪声过程。LQG控制问题就是求取式13能够最小化的最优控制信号u(t)。

设计 LQG控制器一般分为两个步骤[16]。第一步需要得到一个线性二次调节器（LQR），在不考虑dω和nω的情况下寻找得到一个最优控制器，即

需要注意的是，式中要求x可量测并可用于反馈，但实际情况有些状态变量不能直接测量，所以需要第二步寻求状态x的最优估计，这个最优状态估计由Kalman滤波器给出，并且与Q和R无关。用代替x就可获得LQG问题的解，即

根据上述方法设计的 LQG控制器不具有积分作用，所以在设计状态反馈调节器之前，利用图4所示结构给控制对象 FSM 添加一个积分器使系统无稳态误差。

图4 带积分作用的LQG控制器Fig.4 LQG controller with integral action

根据上述结构对FSM设计带有积分作用的LQG控制器，如式(16)所示：

式中：Ki为积分器增益；Kx为最优增益矩阵；L为Kalman滤波器的增益矩阵。带入具体数值可得LQG控制器如式(17)所示：

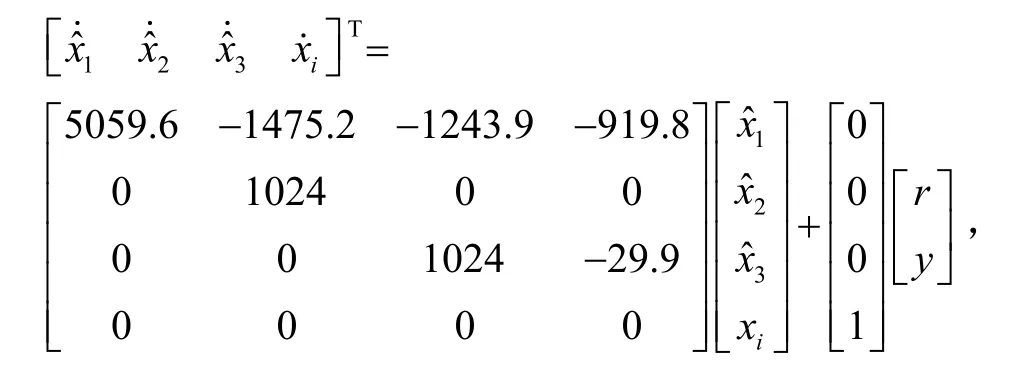
系统在该 LQG控制器的作用下，闭环阶跃响应和开环频率响应如图5所示。

由 LQG控制系统的闭环阶跃响应图可以得到系统的响应时间为0.04 s，无稳态误差；由开环伯德图可以得到，系统带宽为43.8 Hz，系统幅值裕度为3.28 dB，相角裕度为78.03，系统稳定。

图5 在LQG控制器作用下的系统特性Fig.5 System performance with LQG controller

3.3 系统对扰动的抑制仿真结果

闭环控制系统的扰动抑制曲线如图6所示，由图中可以看出：在PID控制器的作用下，系统对扰动的抑制能力主要在10 Hz以下；在LQG控制器作用下，系统的抑制能力可以达到40 Hz，而且抑制能力比PID控制器的抑制能力强。这是因为系统的状态变量受到扰动影响，LQG控制器中的Kalman状态观测器可以处理系统与观测中的扰动问题，使状态估计误差的协方差最小，而PID控制器并没有这个功能，所以PID控制器在克服扰动影响方面比LQG控制器差些。

经过 FSM 系统抑制后的残余功率谱密度可由式(18)计算：

式中：E(f)为FSM系统的误差传递函数；S(f)为空间望远镜受到振动的PSD函数。选取图1中OICETS卫星振动数据，计算得到残余功率谱密度θremains后，再根据式(2)进行计算，计算结果如表3所示。

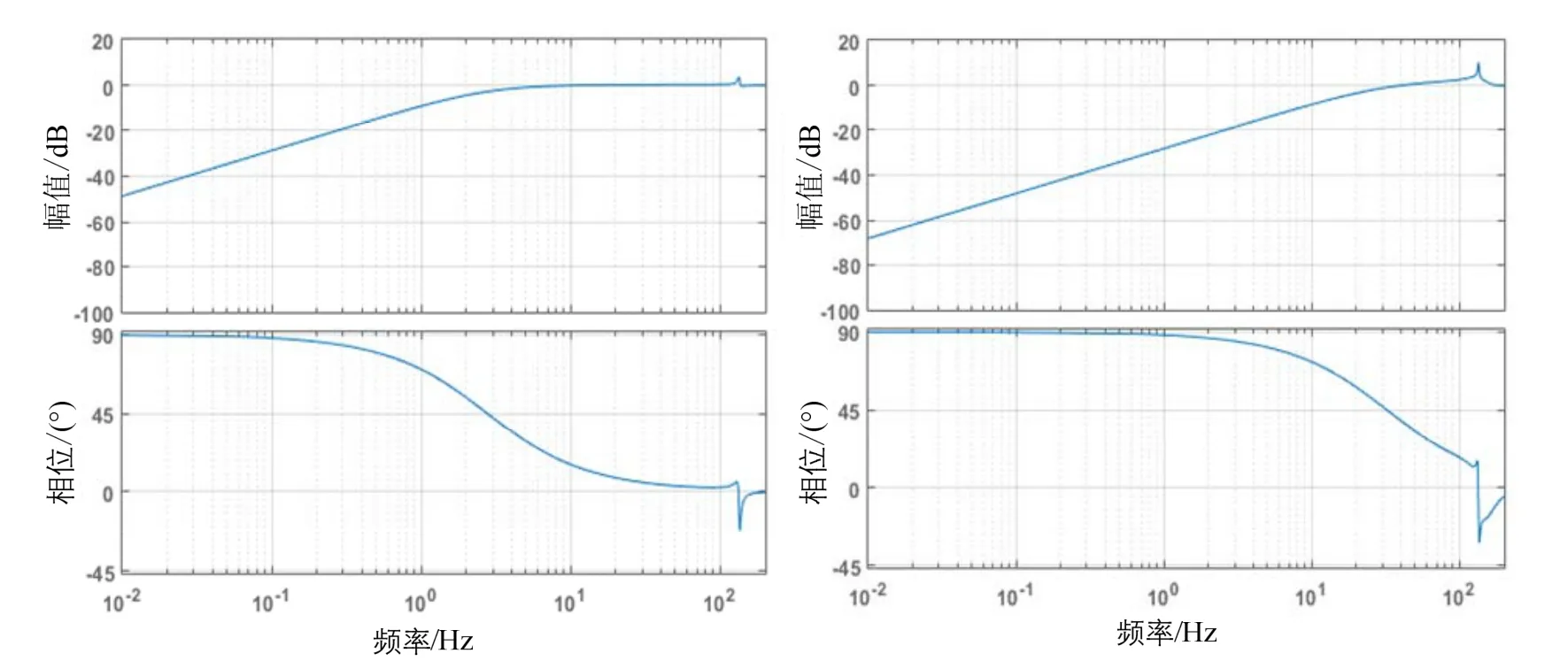
图6 系统分别在PID控制器和LQG控制器作用下的抑制特性曲线Fig.6 Curves of system error rejection with PID controller and LQG controller

根据图6和表3可以看出，跟踪模式和瞄准模式振动数据在0～10 Hz范围内的PSD值的均方根值分别为22μrad和42μrad，经过大口径FSM系统以后，振动被抑制：在PID控制器的作用下，抑制后PSD值的均方根值分别为4.1μrad和12.6μrad，抑制效果分别为14.5 dB和10.3 dB；在LQG控制器的作用下，抑制后PSD值的均方根值分别为0.53μrad和2.75μrad，抑制效果分别为32.5 dB和23.6 dB。

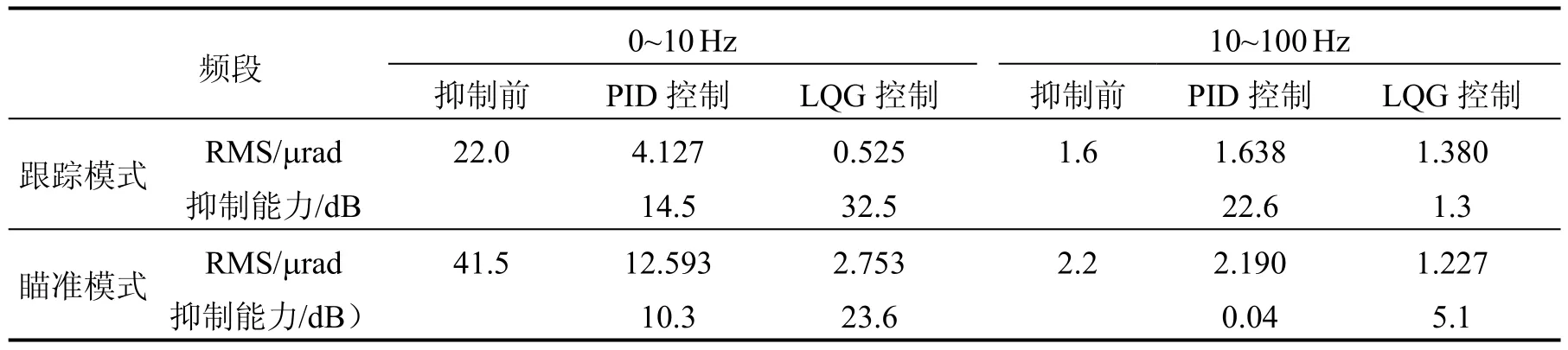
表3 系统抑制前后数据Tab.3 Data before and after system suppressed

4 结 论

大口径 FSM 系统对于抑制空间望远镜低频扰动有着关键作用，本文分别采用最优PID算法和带积分作用的LQG算法对空间望远镜的大口径FSM系统设计控制器，选择OICETS卫星振动数据作为扰动输入对所设计的控制器作用进行验证。仿真结果表明，系统在PID控制作用下的响应时间为0.4 s, 在LQG控制作用下的响应时间为0.04 s，且都无稳态误差。在低频段0～10 Hz的范围内，所设计的FSM系统在完成系统跟瞄任务的同时，可以对该频段扰动有很好的抑制作用。跟踪模式时，系统在PID控制器作用下，抑制能力为14.5 dB，系统在LQG控制器作用下，抑制能力为32.5 dB；瞄准模式时，系统在PID控制器作用下，抑制能力为10.3 dB，系统在LQG控制器作用下，抑制能力为23.6 dB。该大口径FSM系统在LQG控制下系统性能明显高于在ITAE指标最优情况下的PID控制。

（References）：

[1]谭天乐, 朱春艳, 朱东方, 等. 航天器微振动测试、隔离、抑制技术综述[J]. 上海航天, 2014, 31(6): 36-51.Tan Tian-le, Zhu Chun-yan, Zhu Dong-fang, et al. Overview of micro-vibration testing, isolation and suppression technology for spacecraft[J]. Aerospace Shanghai, 2014,31(6): 36-51.

[2]曹小涛, 孙天宇, 赵运隆, 等. 空间大口径望远镜稳像系统发展现状及趋势[J]. 中国光学, 2014, 7(5): 739-748.Cao Xiao-tao, Sun Tian-yu, Zhao Yun-long, et al. Current status and development tendency of image stabilization system of large aperture space telescope[J]. Chinese Optics,2014, 7(5): 739-748.

[3]Sudey J, Schulman J R. In orbit measurements of Landsat-4 thematic mapper dynamic disturbances[J]. Acta Astronaut, 1985, 12: 485-503.

[4]Wittig M, van Holtz L, Tunbridge D E L, et al. In-orbit measurement of microaccelerations of ESA’s communication satellite OLYMPUS[C]//Proc. SPIE, 1990, 1218:205-214.

[5]Marchante E M, Munoz L. ARTEMIS satellite microvibrations testing and analysis activities[C]//Proc. 48th International Astronautical Congress. Torino, Italy, 1997.

[6]Toyoshima M, Araki K. In-orbit measurements of short term attitude and vibrational environment on the Engineering Test Satellite VI using laser communication equipment[J]. Opt. Eng., 2001, 40(5): 827-1832.

[7]Jono T, Toyoshima M, Takahashi N, et al. Laser tracking test under satellite microvibrational disturbances by OICETS ATP system[C]//Proc. SPIE: Acquisition, Tracking, and Pointing XVI. 2002, 4714: 97-104.

[8]Kamiya T, Ogura N, Lkebe K, et al. On-orbit evaluation of OICETS microvibration[C]//Proc. 51st Space Sciences and Technology Conference. Japan Society of Aeronautical Space Sciences, Sapporo, 2007, 3E02: 1-6.

[9]王站. 颤振对星载TDICCD相机成像质量的影响分析[D]. 北京: 中国科学院大学, 2014.Wang Zhan. Platform jitter effect on image quality of spaceborne TDICCD Camera[D]. Beijing: University of Chinese Academy of Sciences, 2014.

[10]凡木文, 黄林海, 李梅, 等. 压电倾斜镜的高压驱动及高速控制[J]. 光学精密工程, 2015, 23(10): 2803-2809.Fan Mu-wen, Huang Lin-hai, Li Mei, et al. High-voltage drive and control for piezoelectric fast steering mirror[J].Optics and Precision Engineering, 2015, 23(10): 2803-2809.

[11]史少龙. 空间望远镜精密稳像控制关键技术研究[D].北京: 中国科学院大学, 2014.Shi Shao-long. Research on control technology of precision image stabilization system in space telescope[D].Beijing: University of Chinese Academy of Sciences, 2014.

[12]Guo Quanfeng, Li Wei, Dong Jihong, et al. Space focusing mirror assembly with flexure hinges[C]//Proc. SPIE. 2014,9283: 928306.

[13]史少龙, 尹达一, 龚惠兴. 大口径快摆镜机构系统辨识及控制参数优化[J]. 中国惯性技术学报, 2014, 22(2);161-166.Shi Shao-long, Yin Da-yi, Gong Hui-xing. Large-aperture fast steering mirror system identification and controller parameter optimization[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 161-166.

[14]Li H W. Study on the servo system of large telescope based on the internal model PID control strategy[C]//Proceedings of the 10th International Conference on Electronic Measurement and Instruments. Chengdu, China,2011: 68-72.

[15]Maurya K, Bongulwar M R, Patre B M. Tuning of fractional order PID controller for higher order process based on ITAE minimization[C]//2015 Annual IEEE India Conference.

[16]Tahir1 F, Ohtsuka T. Using inverse linear quadratic method for systematic tuning of performance index in nonlinear model predictive control[C]//SICE Annual Conference. Akita University, Akita, Japan, 2012.

Large-aperture fast-steering mirror control system of space telescope based on optimal PID and LQG algorithms

ZHANG Xi-dan1,2, WEI Chuan-xin1,2, YIN Da-yi1,2
(1. University of Chinese Academy of Sciences, Beijing 100039, China;2. Shanghai Institute of Technical Physics of the Chinese Academy of Sciences, Shanghai 200083, China)

The observation by space telescope is subject to uncertain disturbances with small vibration swing and wide frequency bandwidth. These disturbances are hard to be controlled, and most of them are within 10 Hz. In order to reduce these low-frequency disturbances, a controller with large-aperture fast-steering mirror system is designed. A PID algorithm at the condition of optimal integrated time absolute error (ITAE)criterion and a LQG algorithm with integral action are used respectively in designing the controller. A simulation model based on Simulink platform is built, and the simulation results show that the PID controller and the LQG controller have good performances in dynamic response and steady-state response. Meanwhile they can effectively suppress the low-frequency disturbances. The response time is 0.4 s and 0.04 s when the system is controlled by the PID and the LQG respectively, and the system is without steady state error in both situations. The vibration power spectrum density data of OICETS satellite verify the suppression ability of the system. In low-frequency range of 0-10 Hz: under the tracking mode, the disturbance restrain ability of the systems with PID controller and with LQG controller are 14.5 dB and 32.5 dB, respectively; while under targeting mode, the disturbance restrain ability of the systems with PID controller and with LQG controller are 10.3 dB and 23.6 dB, respectively. The comparison results indicate that the LQG controller has a better performance than the optimal PID controller in large-aperture FSM system.

large-aperture fast steering mirror; disturbance suppression; PID algorithm; LQG algorithm

U666.1

A

1005-6734(2016)05-0677-05

10.13695/j.cnki.12-1222/o3.2016.05.021

2016-04-26；

2016-06-16

国家自然科学基金资助项目（40776100）

张茜丹（1991—），女，博士研究生，从事空间高精度稳像控制算法方面的研究。E-mail: zh_xidan@163.com

联 系 人：尹达一（1976—），男，博士生导师。E-mail: yindayi@mail.sitp.ac.cn