不完美维护活动干预下的设备剩余寿命估计

胡昌华，裴 洪，王兆强，张正新，周绍华

（火箭军工程大学 302教研室，西安 710025）

不完美维护活动干预下的设备剩余寿命估计

胡昌华，裴 洪，王兆强，张正新，周绍华

（火箭军工程大学 302教研室，西安 710025）

剩余寿命估计是保障设备安全性和可靠性的关键技术。现有文献在研究维护活动干预下的设备剩余寿命估计问题时，通常仅考虑维护活动对退化水平或退化速率的单一影响，忽略了维护活动对两者的双重影响。鉴于此，提出了一种考虑不完美维护活动影响的性能退化建模与剩余寿命估计方法，融合了维护活动对设备退化水平和退化速率的双重影响。首先基于扩散过程分阶段建立存在不完美维护活动干预下的随机退化模型，然后基于设备的状态监测数据和维护数据对模型参数进行极大似然估计和Bayesian更新，最后在首达时间的概念下，推导得到了剩余寿命的解析概率分布。实验结果表明，所提出方法能够大大提高存在不完美维护活动影响设备的剩余寿命估计精度。

不完美维护；剩余寿命估计；扩散过程；首达时间

随着现代科学技术的迅猛发展，工程设备朝着复杂化和智能化的方向发展，从而对设备的可靠性提出了更高的要求。尤其在航空航天和武器系统等领域，由于设备失效引发的事故会造成不可估量的人员伤亡和财产损失[1]。为确保工程设备安全稳定运行，预测与健康管理（Prognostics and health management,PHM）成为当前研究的热点问题。剩余寿命（Remaining useful life, RUL）估计作为PHM的关键环节，近年来得到研究者们的广泛关注，涌现出了大量的研究成果[2-4]。

现有的 RUL估计方法分为基于失效物理的方法和数据驱动的方法[5]。由于实际设备的复杂程度通常较高，往往难以对其退化机理进行准确建模，使得数据驱动的方法成为当前研究中的主流方法[3]。现有数据驱动的方法大致可分为传统的 RUL估计方法和基于退化建模的RUL估计方法。传统的RUL估计方法通过分析寿命数据确定设备寿命的概率分布。一方面，传统的 RUL估计方法无法刻画出设备间的个体差异性；另一方面，随着设备可靠性的不断提高，通常难以获取足够的寿命数据。基于退化建模的方法能充分利用设备的状态监测信息，如振幅、疲劳裂纹长度、电子器件参数漂移、电池容量大小、油液分析数据等，不仅能够降低实验成本，而且可有效提高RUL估计精度。Lu和Meeker较早利用随机系数回归模型描述设备退化过程，并提出了一种模型参数估计的两步法[6]。为刻画退化过程的随机性，Singpurwalla等提出采用随机过程描述设备退化过程，进而实现设备RUL的估计[7]。Si等对基于退化建模的剩余寿命估计方法进行了较为系统的综述[3]。

为简化起见，现有退化建模和RUL估计研究几乎均假定设备在寿命周期内不存在任何维护活动或维护活动为完美维护活动，而工程实际中大部分维护活动为不完美维护活动。鉴于此，对于寿命周期内存在不完美维护活动干预的设备，上述方法的适用范围受到了限制，无法实现该类设备RUL的准确估计。

根据修复程度不同可大致将维护活动分为三类：完美维护、不完美维护和小修[8]。在工程实际中，大部分维护活动均为不完美维护，即系统的退化指标通过维护活动无法恢复至全新的状态，只能恢复至修复如新和修复如旧之间的某一状态[8]，因此，相对于完美维护和小修，不完美维护更具一般性，如为钻头喷洒润滑剂，对钢厂风机进行动平衡调整，对陀螺仪漂移系数进行调整校正等等。不完美维护活动通常能够减缓设备的退化过程，进而延长设备的寿命。显然，不完美维护活动对RUL的估计有着极其重要的影响，如何在考虑不完美维护活动干预下进行退化建模和RUL估计成为当前亟需解决的难题。近年来，研究者们提出了许多不完美维护活动模型，并将不完美维护活动融入设备的RUL估计中。现有研究中，不完美维护活动的影响一般可以用虚拟年龄[9-10]和失效率[11-13]的变化进行描述。Zhou结合这两种方法提出了一种混合模型来刻画维护活动[14]。上述不完美维护模型均以最优维护策略的制定为目的，但并未涉及RUL估计的研究。You等采用拓展比例风险模型对维护活动进行了仿真分析，得到了RUL的均值和方差[15]。Shi等采用随机滤波理论将RUL估计与不完美维护策略结合，建立被监测设备不完美维修策略下的实时 RUL估计模型[16]。Wang等采用带有负跳变的Wiener过程对维护活动干预下的设备RUL进行估计，但仅考虑了维护活动对退化量（或退化水平）的影响，没有考虑对退化率（或退化速率）的影响[17]。Zhang等基于扩散过程进行寿命估计时考虑了维护活动对退化率的影响，但却没有考虑维护活动对退化量的影响[18]。

不完美维护活动对退化量和退化率都有着一定的影响，为了刻画不完美维护活动的影响，准确进行RUL估计，必须将这两个因素同时考虑进去。鉴于此，本文针对寿命周期内存在不完美维护活动干预的设备，提出了一种考虑不完美维护影响的退化建模与RUL估计方法，融入了不完美维护活动对设备退化量和退化率的双重影响。首先基于扩散过程分阶段建立存在不完美维护活动干预下的随机退化模型；然后基于状态监测数据对模型参数进行极大似然估计和Bayesian更新，进一步在首达时间的概念下，推导得到RUL的解析概率分布；最后通过陀螺仪的实例验证了本文方法的有效性和优越性。

1 问题描述

在工程实际中，通过状态监测技术能够获得设备当前的退化水平，通过比较当前退化水平与预防性维护阈值进行维护决策，当其超出预防性维护阈值时进行维护活动。预防性维护活动一方面能够使退化水平恢复至“修如新”和“修如旧”之间的某一状态，可以用残余退化量进行刻画；另一方面又会加快设备的退化速度[19]。需要指出的是，本文研究中所提到的预防性维护活动均指不完美维护活动。为了保证设备的运行可靠性和经济可承受性，工程实际中通常会限制维护活动的次数n，退化过程可以划分为n+1阶段。在第n+1阶段内，若设备的退化水平达到了预先设定的失效阈值，则意味着设备发生失效，为了避免财产损失和事故发生，此时需要对设备进行替换活动，如图 1所示。

在图1中，横坐标为设备的运行时间t，纵坐标为设备的退化量X( t)，ωp为预防性维护阈值，ω为设备的失效阈值，Ti为第i次维护时刻。监测时刻用ti,j表示，i为ti,j前经历的维护次数，i∈ N+，j为第i次维护后进行的监测次数，间进行的监测总数。显然，描述的为同一时刻。另外，由于设备运行中磨损等不可逆因素，这里假定每次维护后的残余退化量和退化率随着维护次数的增多而增加，这在实际中也较为常见。

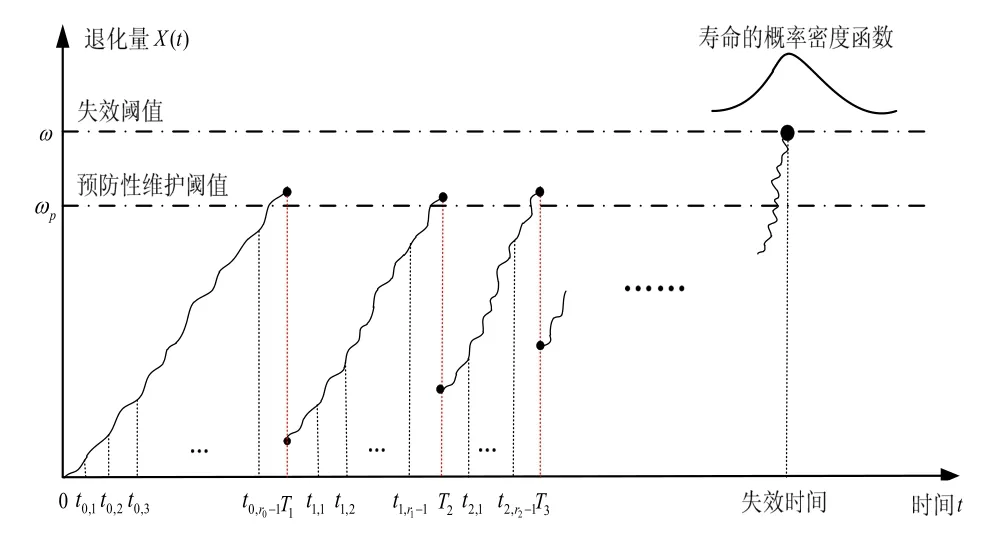
图1 维护活动干预下的设备退化轨迹Fig.1 Degradation trajectory of the equipment under intervention of maintenance activities

基于以上描述，本文主要研究以下几个问题：

1） 如何建立存在不完美维护活动干预的设备性能退化模型；

2） 如何基于设备的状态监测数据和维护数据对所构建的退化模型参数进行估计；

3） 如何在首达时间的意义下，推导RUL概率分布，实现设备RUL的估计。

2 不完美维护活动干预下的退化建模

基于扩散过程的退化模型是一类常见的随机退化模型，在机械磨损、设备腐蚀等退化过程描述中得到广泛应用[3,17,20-21]。本文采用扩散过程分阶段构建维护活动干预下的非线性随机退化模型，拟合设备的实际退化过程，经过i次维护活动后，设备退化量可以表示为

式中：X( t)为设备在t时刻的退化量；i为t时刻前设备已经历的维护次数；iη刻画第i次维护后的残余退化量系数，且，a、b为超参数；pω为预防性维护阈值，一般由工业标准和专家经验确定；为第i次维护后漂移系数，且漂移系数的参数向量，iλ刻画设备间的个体差异性，θ表征同类设备的共性。值得注意的是，iλ是随着维护次数的增加而发生变化的，且满足，其中，0λ表征第一次维护前设备间的个体差异性，ci表示第i次维护后退化率变化因子，其PDF为为ci的分布参数，且c0=1；Ti为第i次维护时刻，Bσ为扩散系数，B(·)为标准布朗运动。

通过上述分析，对于式(1)给出的随机退化过程，基于首达时间的概念，在第n+1阶段内tn,j时刻的RUL可以定义为式中：xn,j为tn,j时刻的退化观测值；n为tn,j之前经历维护活动的次数；j为第n次维护后进行监测次数；ω为失效阈值。

式中：Ω为cn的取值空间，为cn的PDF。

3 参数估计和剩余寿命估计

3.1 残余退化量系数的估计

对式(5)取对数，可得：

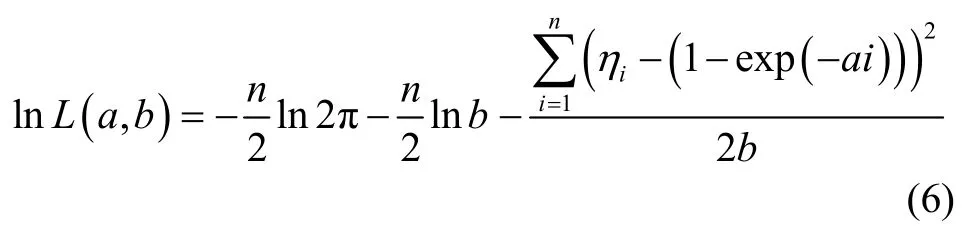
为了最大化对数似然函数，将式(6)对b求偏导，可得：

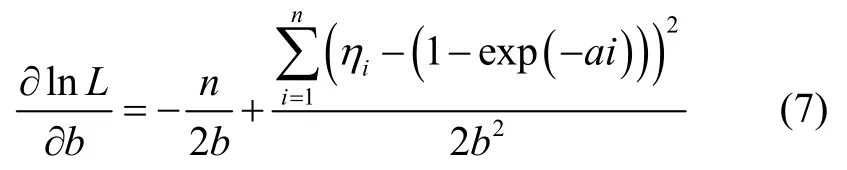
令偏导为0，可以推导出a b、的隐式关系：

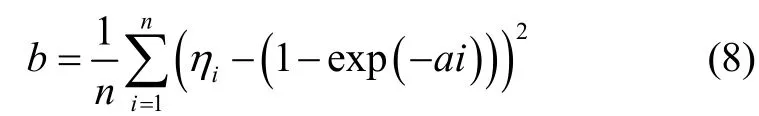
将式(8)代入式(6)表示的对数似然函数中，可以得出剖面对数似然函数lnL( a)。最大化lnL( a)可以得到参数a的极大似然估计。进一步将a的估计值代入式(8)，即可得到参数b的极大似然估计。

3.2 退化参数的估计

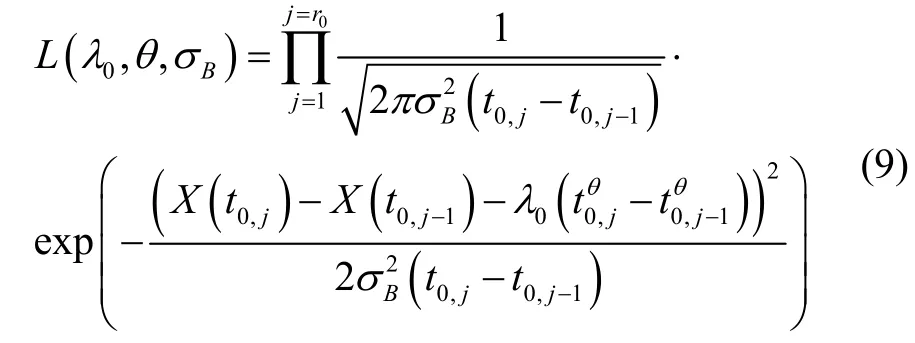
式中：r0为第一次维护前进行的监测次数；和分别表示t0,j和t0,j-1时刻监测到的退化值。

证明：基于扩散过程的基本性质有：

根据Bayesian链式法则有：

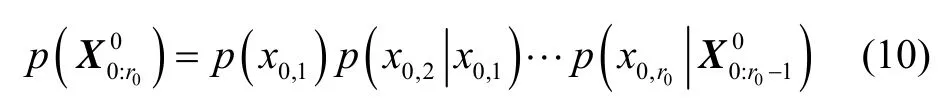
证毕。

3.3 维护参数的估计

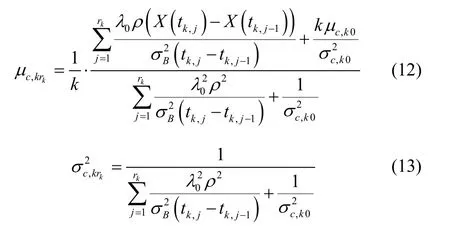
证明：根据式(1)描述的退化模型和扩散过程的基本性质，在随机参数ck给定的条件下有：

基于Bayesian链式法则，在随机参数ck给定的条件下可以确定退化数据的联合概率密度：

令ck的先验分布为，其均值为 kμc,k0，方差为能够通过k-1次维护后的参数更新得到。

根据Bayesian定理，随机参数ck的后验分布可以通过下式得到：

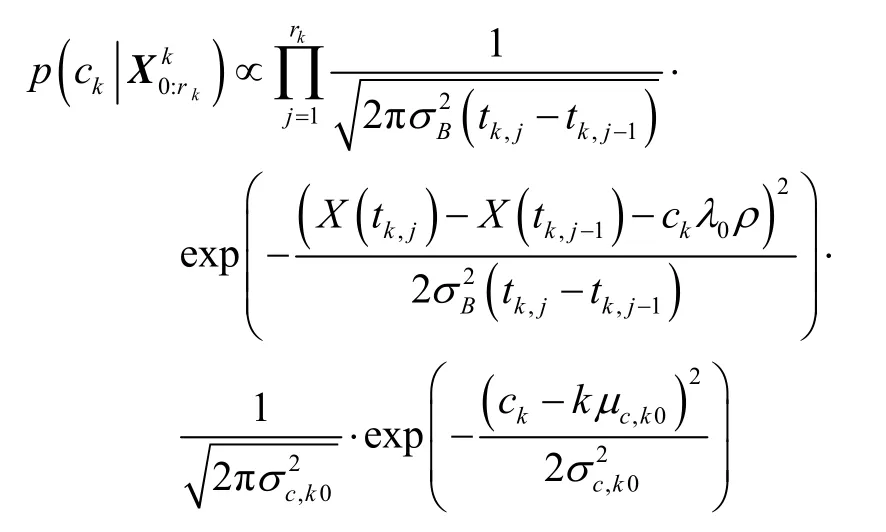
证毕。

为了进一步概括上述参数的估计过程，可得到基于极大似然估计和Bayesian推理的退化模型参数估计算法如下。

步骤 1：基于每次维护后获取的历史残余退化数据，对参数(a, b)进行极大似然离线估计；

步骤4：通过式(12)和式(13)实时对进行参数更新；若在某一时刻进行了维护活动，则此时刻的更新结果可作为下一阶段更新的初始值；

3.4 剩余寿命的估计

根据式(2)描述的RUL，在随机参数cn为给定，基于文献[21]，可以推导出tn,j时刻RUL的条件PDF的解析表达式：

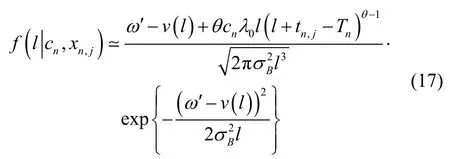
考虑cn为随机性，基于式(3)可以推导出RUL的PDF的解析表达式，为此需首先给出如下引理。

引理 1[20]若，且，则：

基于上述引理，可推导得到设备在tn,j时刻 RUL的PDF的解析形式表达式。

定理3 对于式(1)给出的随机退化过程，基于首达时间的概念，设备在第n+1阶段内tn,j时刻RUL的PDF的解析表达式为

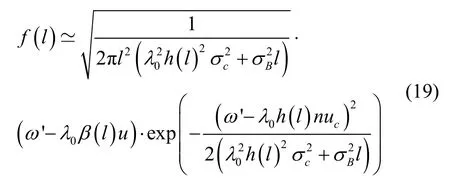
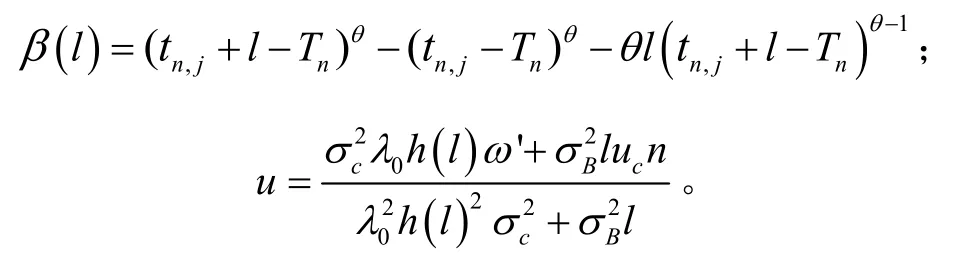
证明：利用引理1的结论，将式(12)、(13)和(17)代入式(3)，得：

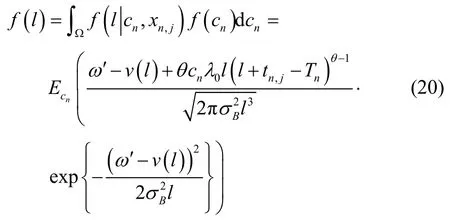
式(20)的表示形式与引理 1相一致，可以直接得出定理3描述的结论。

证毕。

将前面估计得到的参数代入式(19)，即可实现RUL的估计。

4 实验研究

陀螺仪作为战略导弹惯性导航系统的核心设备，其性能好坏直接影响着制导精度。在实际工程中，陀螺仪不可避免地受到内部转轴磨损和外部环境变化的综合影响，陀螺仪的漂移系数呈现出增大的趋势。当陀螺仪的漂移系数超出预先设定的预防性维护阈值后，安装在惯导系统底部的陀螺漂移硬件补偿电路通过调整陀螺仪力矩器线圈上的电流，能够对陀螺漂移的常值项和一次项进行补偿，从而提高陀螺仪的精度。陀螺仪漂移系数的校正可理解为广义上的维护活动，通常需协调生产厂家在使用单位进行此类维护活动，由于工程中的维护活动大都是不完美的，因而维护后的残余退化量和退化率是逐次增大的。当维护效果无法满足陀螺仪的使用要求时，将对陀螺仪进行更换处理，因此维护次数是有限的。

下面采用本文提出的方法对某型导弹惯性导航系统中液浮陀螺仪的RUL进行估计。在部队实际中，通常约每隔3个月对陀螺仪进行一次通电测试，每次通电测试活动持续时间为2.5 h。通过与部队协调，获取了两组同型号陀螺仪的一次项漂移数据，如图2所示。陀螺仪1的漂移数据主要用于对式(1)所定义的模型参数进行估计，陀螺仪2的漂移数据主要用于对维护参数进行更新并对陀螺仪的RUL进行估计，图中的通电时间指的是陀螺仪的工作时间。退化过程中预防性维护阈值ωp=0.30(°)/h，失效阈值ω= 0.37(°)/h，该失效阈值是在导弹设计阶段通过大量试验确定的，在实际工程中被严格执行，退化过程共经历3次校正维护。从图2可以直观地看出，陀螺仪1共有115组漂移数据，实际使用寿命为277.5 h的通电时间，陀螺仪2共有113组漂移数据，实际使用寿命为282.5 h的通电时间。陀螺仪的漂移系数是逐渐增大的，当漂移系数超过预防性维护阈值时，考虑到陀螺仪的稳定性和可靠性要求，需要对陀螺仪进行调整校正，即预防性维护活动。陀螺仪经历了预防性维护活动后，漂移系数未回归到 0，存在着一定的残余量且退化速率得到了进一步加快，意味着预防性维护活动是不完美维护活动，对退化量和退化速率均有着一定的影响，预防性维护的效果随着维护次数增加逐渐减弱。根据工程实践经验，陀螺仪所经历预防性维护的次数一般设定为3次。

图2 维护活动干预下陀螺仪的漂移数据Fig.2 Drift data of gyroscope under intervention of maintenance activities

根据第3节中参数估计算法，利用陀螺1的漂移数据对模型参数进行估计，参数的估计结果如表1所示。

表1 退化参数的估计结果Tab.1 Estimation results of degradation parameters

为了验证本文所提出的维护活动干预下 RUL估计方法的有效性，将本文所提出的同时考虑维护活动对退化量和退化率影响的方法记为M1，将不考虑维护活动对退化率影响的方法记为M2。

为了便于分析，经过 3次维护后，选择时刻集｛260,262.5,265,267.5, 270,272.5,275,277.5,280｝ 作为RUL的估计时刻，分别采用两种方法对陀螺仪 2的RUL进行估计，陀螺仪的 RUL期望可表示为则两种方法下的RUL期望值及相对误差如表2所示。

表2 两种方法的RUL期望值及相对误差Tab.2 Expected values and relative errors of RULs by the two methods

从表2可以看出：方法M2估计的RUL期望与实际RUL之间偏差很大，无法准确估计陀螺仪的RUL；方法M1估计的RUL期望与实际RUL之间偏差较小，能够有效反映陀螺仪的健康状况，因而在对考虑维护活动干预下的陀螺仪进行RUL估计时，需要考虑维护活动对退化量和退化率的双重影响。

为直观比较两种方法的差异，下面绘制出两种方法在各估计时刻的RUL的PDF曲线，并绘制出相应的RUL期望值，如图3和图4所示。

图3 方法M1估计的陀螺仪的RULFig.3 Gyroscope’s RUL estimated by method M1

图4 方法M2估计的陀螺仪的RULFig.4 Gyroscope’s RUL estimated by method M2

通过比较图3和图4可以看出：方法M1估计的RUL期望更加接近实际 RUL，随着退化数据不断获取，RUL的PDF曲线越来越高，说明RUL估计的不确定性越来越小；方法M2估计的RUL期望严重偏离了实际RUL，主要原因是没有考虑维护活动对退化率的影响，高估了陀螺仪的RUL，这在实际工程中可能会造成灾难性事故。

为进一步定量比较RUL估计的效果，引入RUL估计的均方误差指标：

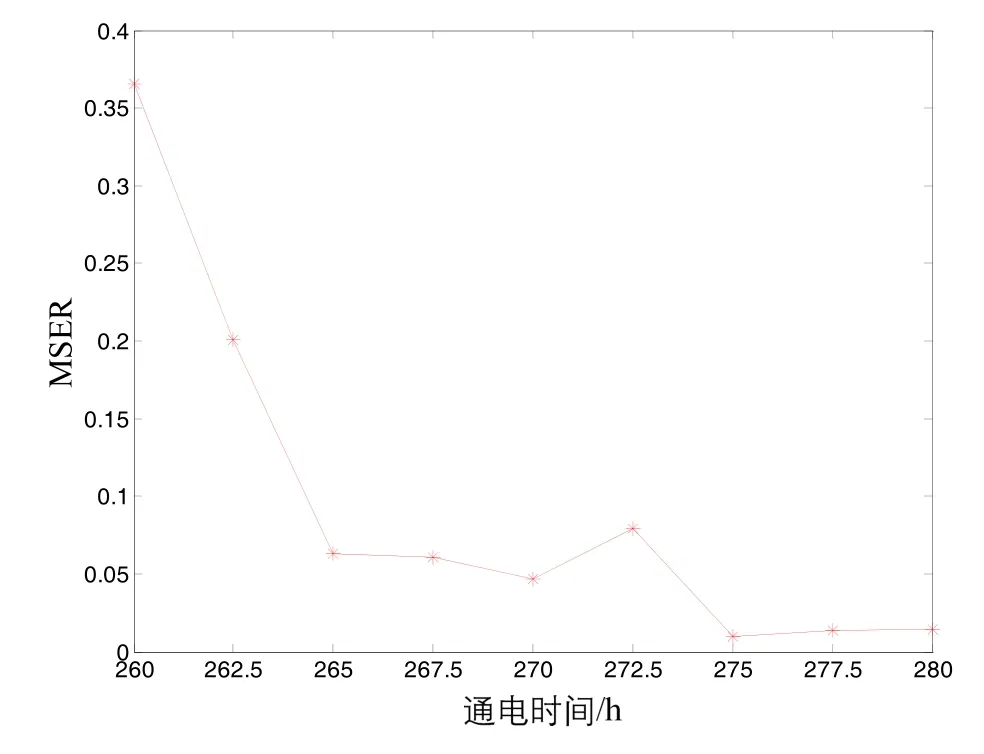
图5 方法M1在估计时刻的均方误差Fig.5 MSE at estimation time by method M1

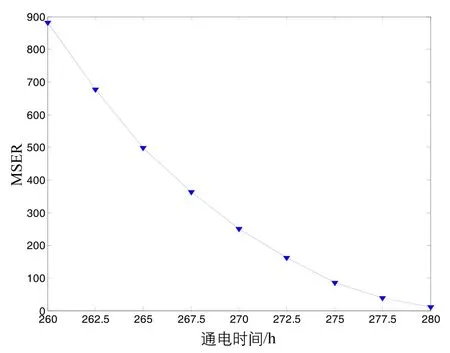
图6 方法M2在估计时刻的均方误差Fig.6 MSE at estimation time by method M2

5 结 论

本文针对寿命周期内存在不完美维护活动的设备，提出了一种同时考虑不完美维护活动对退化量和退化率影响的退化建模和RUL估计方法，给出了参数估计的方法，并推导得到了RUL的PDF的解析表达式。最后，通过陀螺仪的实例对本文方法进行了验证。实验研究表明：1）本文提出的方法能够实现最后一个阶段内设备RUL的准确估计，对设备的替换决策具有指导性作用；2）相对于以往文献中的RUL估计方法，本文提出的方法，不仅考虑了维护活动对退化量的影响，而且考虑了维护活动对退化率的影响，大大提高了RUL的估计精度，保证了均方误差均小于0.4，具有潜在的工程应用价值。

（References）：

[1]周东华, 魏慕恒, 司小胜. 工业过程异常检测、寿命估计与维修决策的研究进展[J]. 自动化学报, 2013, 39(6):711-722.Zhou Dong-hua, Wei Mu-heng, Si Xiao-sheng. A survey on anomaly detection, life prediction and maintenance decision for industrial processes[J]. Acta Automatica Sinica, 2013, 39(6): 711-722.

[2]李瑞, 汪立新, 刘刚, 等. 基于加速退化模型的加速度计非线性特征分析及贮存寿命预测[J]. 中国惯性技术学报, 2014, 22(1): 125-130.Li Rui, Wang Li-xin, Liu Gang, et al. Nonlinear characteristic analysis and storage life forecast for accelerometer based on accelerate degradation model[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 125-130.

[3]Si X S, Wang W B, Hu C H, et al. Remaining useful life estimation — A review on the statistical data driven approaches[J]. European Journal of Operational Research,2011, 213(1): 1-14.

[4]李明福, 胡昌华, 周志杰, 等. 基于退化数据的贮存设备最优检测策略[J]. 系统工程与电子技术, 2015, 37(5):1219-1223.Li Ming-fu, Hu Chang-hua, Zhou Zhi-jie, et al. Optimal inspection policy of storage equipment based on the degradation data[J]. Systems Engineering and Electronics,2015, 37(5): 1219-1223.

[5]Pecht M G. Prognostics and health management of electronics[M]. New Jersey: John Wiley Publishing Company, 2008.

[6]Lu C J, Meeker W Q. Using degradation measures to estimate a time-to-failure distribution[J]. Technometrics,1993, 35(2): 161-174.

[7]Singpurwalla N D. Survival in dynamic environments[J].Statistical Science, 1995, 10(1): 86-103.

[8]Pham H, Wang H. Imperfect maintenance[J]. European Journal of Operational Research, 1996, 94(3): 425-438.

[9]Malik M. Reliable preventive maintenance scheduling[J].AIIE Transactions, 1979, 11(3): 221-228.

[10]Yeh R H, Chang W L, Lo H C. Optimal threshold values of age and two-phase maintenance policy for leased equipments using age reduction method[J]. Springer Science, 2010, 181(1): 171-183.

[11]Kvam P H, Singh H, Whitaker L R. Estimating distributions with increasing failure rate in an imperfect repair model[J]. Lifetime Data Analysis, 2002, 8(8)：53-67.

[12]Pongpech J, Murthy. Optimal periodic preventive maintenance policy for leased equipment[J]. Reliability Engineering and System Safety, 2006, 91(7): 772-777.

[13]Nakagawa T, Mizutani S. A summary of maintenance policies for a finite interval[J]. Reliability Engineering and System Safety, 2009, 94(1): 89-96.

[14]Zhou X, Xi L, Lee J. Reliability-centered predictive maintenance scheduling for continuously monitored system subject to degradation[J]. Reliability Engineering and System Safety, 2007, 92(4): 530-534.

[15]You M Y, Meng G. Residual life prediction of repairable systems subject to imperfect preventive maintenance using extended proportional hazards model[J]. Journal of Process Mechanical Engineering, 2012, 226(1): 50-63.

[16]石慧, 曾建潮. 考虑非完美维修的实时剩余寿命预测及维修决策模型[J]. 计算机集成制造系统, 2014, 20(9):2259-2266.Shi Hui, Zeng Jian-chao. Predicting of remaining useful life and maintenance decision model considering imperfect preventive maintenance[J]. Computer Integrated Manufacturing Systems, 2014, 20(9): 2259-2266.

[17]Wang Z Q, Hu C H, Wang W B, et al. A simulation-based remaining useful life prediction method considering the influence of maintenance activities[C]//2014 IEEE Conference on Prognostics and Health Management (PHM). 2014: 284-289.

[18]Zhang M M, Olivier G, Xie M. Degradation-based maintenance decision using stochastic filtering for systems under imperfect maintenance[J]. European Journal of Operational Research, 2015, 245(3): 531-541.

[19]Van P D, Voisin A, Levrat E, et al. Remaining useful life based maintenance decision making for deteriorating systems with both perfect and imperfect maintenance actions[C]//2013 IEEE Conference on Prognostics and Health Management (PHM). 2013: 1-9.

[20]Si X S, Wang W B, Hu C H, Zhou D H. Remaining useful life estimation based on a nonlinear diffusion degradation process[J]. IEEE Transactions on Reliability,2012, 61(1): 50-67.

[21]Wang Z Q, Hu C H, Wang W B, et al. An additive wiener process-based prognostic model for hybrid deteriorating systems[J]. IEEE Transactions on Reliability, 2014, 63(1):208-222.

Remaining useful lifetime estimation for equipment subjected to intervention of imperfect maintenance activities

HU Chang-hua, PEI Hong, WANG Zhao-qiang, ZHANG Zheng-xin, ZHOU Shao-hua
(Unit 302, Rocket Force University of Engineering, Xi’an 710025, China)

The estimation of equipment’s remaining useful life (RUL) is a key technique to ensure the equipment’s safety and reliability. In studying the influence of maintenance activities on RUL estimation, the current literatures usually assumed that maintenance activities could only have influence on degradation level or degradation speed, but not on both. Aiming at this problem, a degradation modeling and RUL estimation method is proposed by combining the double influences of the imperfect maintenance activities on degradation level and degradation speed. A stochastic degradation model is established based on diffusion process by stages, taking into account the influence of imperfect maintenance activities. The parameters in the degradation model are estimated by maximum likelihood estimation and Bayesian updating method based on the condition monitoring data and the maintenance data of the equipment, and then the analytical probability distribution of RUL is derived based on the concept of first hitting time. Experiment results show that the proposed method could greatly increase the RUL estimation precision for the equipment subjected to intervention of imperfect maintenance activities.

imperfect maintenance; remaining useful life estimation; diffusion process; first hitting time

TP202+.1

A

1005-6734(2016)05-0688-08

10.13695/j.cnki.12-1222/o3.2016.05.023

2016-06-16；

2016-09-02

国家自然科学基金（61573365，61603398，61374120）

胡昌华（1966—），男，教授，博士生导师，从事故障诊断与容错控制，装备预测与健康管理研究。

E-mail: hch6603@263.net