机床导轨滚转角测量误差分析

齐静雅,王昭,黄军辉,余宝,高建民

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安)



机床导轨滚转角测量误差分析

齐静雅1,王昭1,黄军辉1,余宝1,高建民2

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安)

为研究激光外差干涉法滚转角测量中反射器入射角误差对测量灵敏度的影响,利用琼斯矩阵,建立了一种新的测量光路数学模型。新模型在原有模型的基础上考虑了高反镜入射角误差的影响,基于多层介质膜作用机理,量化了高反镜入射角误差引起的反射光变化,进而推导出高反镜入射角误差对滚转角测量灵敏度的影响。结果表明:测量系统的放大倍数随高反镜入射角不同而变化,并在入射角为36°时取得理论最大值720倍,达到高反镜正常角度入射时放大倍数的6倍;实验验证当高反镜入射角为38°时,系统放大倍数达到346倍,若采用分辨率为0.01°的相位计,滚转角的测量分辨率可达0.1″。实验结果验证了理论分析的正确性,并且提供了一种通过改变高反镜入射角来提高滚转角测量灵敏度的思路。

滚转角;高反镜;入射角;测量灵敏度;机床导轨

几何误差检测是数控机床误差补偿技术的关键环节。在三轴数控机床导轨的21项几何误差中,滚转角是目前较难测量的一项。目前基于偏振态的激光外差干涉测量方法研究较多,其原理是基于敏感元件对激光偏振态的敏感性,通过敏感元件的滚转改变激光的偏振态,从而改变拍频信号的相位,由相位计获得相位变化量反推得敏感元件的滚转角[1-8]。文献[5]利用偏振片作为敏感元件,理论放大倍数可达到60倍,此方法的放大倍数较小,测量精度不高。文献[6]利用相位延迟量为178°的波片作为敏感元件,理论放大倍数可达142倍,这里所用波片为非标准波片,需特殊制造。文献[7]使用1/2波片作为敏感元件,并且利用直角棱镜将光路折返,使光束两次通过1/2波片,提高了测量系统的灵敏度,实验验证放大倍数达到了124倍。在之前的工作中,我们发现了直角棱镜作为反射元件造成的相位损失对测量系统的放大倍数有一定的影响,并提出了基于高反膜相长干涉原理的解决方案,使用两个相互垂直的高反镜代替直角棱镜,默认高反镜的入射角为45°[8]。但是,在实际测量中,安装、调节误差的存在使高反镜入射角存在误差,此误差对测量结果的影响程度尚不明确。文献[9]分析了入射角误差在±1°内时反射光的相位变化,认为可忽略不计,本文对其在更大范围内产生的影响进行了完善的分析。

本文基于文献[8]提出的高反镜折返光路系统,利用琼斯矩阵计算建立了相应的数学模型,基于多层介质膜作用机理,分析了高反镜入射角误差引起的高反镜反射光变化,并代入数学模型中得到了高反镜入射角误差对滚转角测量系统放大倍数的影响,通过实验验证了高反镜入射角误差为一定值时,测量系统的灵敏度有所提高。

1 滚转角测量原理

1.1 测量原理

本文所用的测量系统如图1所示。双频氦氖激光器发出正交线偏振光,经分光片分为两束,其中由分光片反射的部分作为参考光,经过检偏器1,被光电探测器1接收后形成参考信号;由分光片透射的部分作为测量光,首先经过1/4波片椭偏化,再经过固定在导轨滑块上的敏感元件1/2波片,经过两个互相垂直的高反镜将光路折返后,再次通过1/2波片后经过检偏器2,最后被光电探测器2接收形成测量信号。当导轨滑块带动1/2波片发生滚转时,测量光的偏振态变化,导致测量信号相对于参考光的相位差发生变化,通过相位计检测相位差变化量即可求得1/2波片即导轨的滚转角。

图1 滚转角测量系统简图

1.2 数学模型

以双频氦氖激光器出射的正交线偏振光电矢量E1和E2的偏振方向为x轴和y轴、激光传播方向为z轴建立坐标系,其中1/4波片快轴与x轴的夹角为θ,1/2波片快轴与x轴的夹角为α,检偏器透光轴与x轴的夹角为45°,则激光束、1/4波片、1/2波片、检偏器和高反镜的琼斯矩阵依次为[8]

式中:rjp和rjs分别为高反镜j反射光的p分量与s分量的幅值反射系数;δjp和δjs分别为高反镜j反射光的p分量与s分量的相位变化量,其大小都与高反镜j的入射角有关。在理想情况下,高反镜1和高反镜2的入射角为45°,此时r1p=r2p≈r1s=r2s≈1,δ1p=δ2p=0,δ1s=δ2s=π。

光电探测器接收到的测量信号为

Em=PH(-α)M2M1H(α)QE0

(1)

将各琼斯矩阵代入式(1),得测量信号的交流分量为

Im(·)=kmcos[(ω1-ω2)t+(φ1-φ2)+ψ]

(2)

式中:km为测量信号光强值;ψ为测量信号的相位变化量

ψ=tan-1(tanθtan4α)+tan-1(cotθtan4α)

(3)

参考信号交流分量与式(2)类似,其相位为式(2)中相位的前两项,因此两信号的相位差即为ψ,相位差ψ与滚转角α的关系如图2所示。求相位差ψ的导数可得曲线的斜率值,在斜率值最大处的局部区域,相位差ψ与滚转角α的关系近似线性,此区域即作为测量的灵敏区,最大的斜率值即为测量系统的放大倍数。

图2 理论相位差ψ与滚转角α的关系图

2 高反镜入射角误差影响分析

2.1 高反镜作用机理

高反镜反射模型如图3所示,其作用机理是基于光波的相长干涉[8]。镀制过程为在基底材料(G)上镀一层高折射率材料薄膜(H),之后镀制低折射率材料薄膜(L),并以此重复叠加,与空气(A)的接触层为高折射率材料。镀制模型为GH(LH)TA,T为镀制的L的层数。当入射角为45°时,反射光的s分量相位变化为π,p分量相位变化为0。

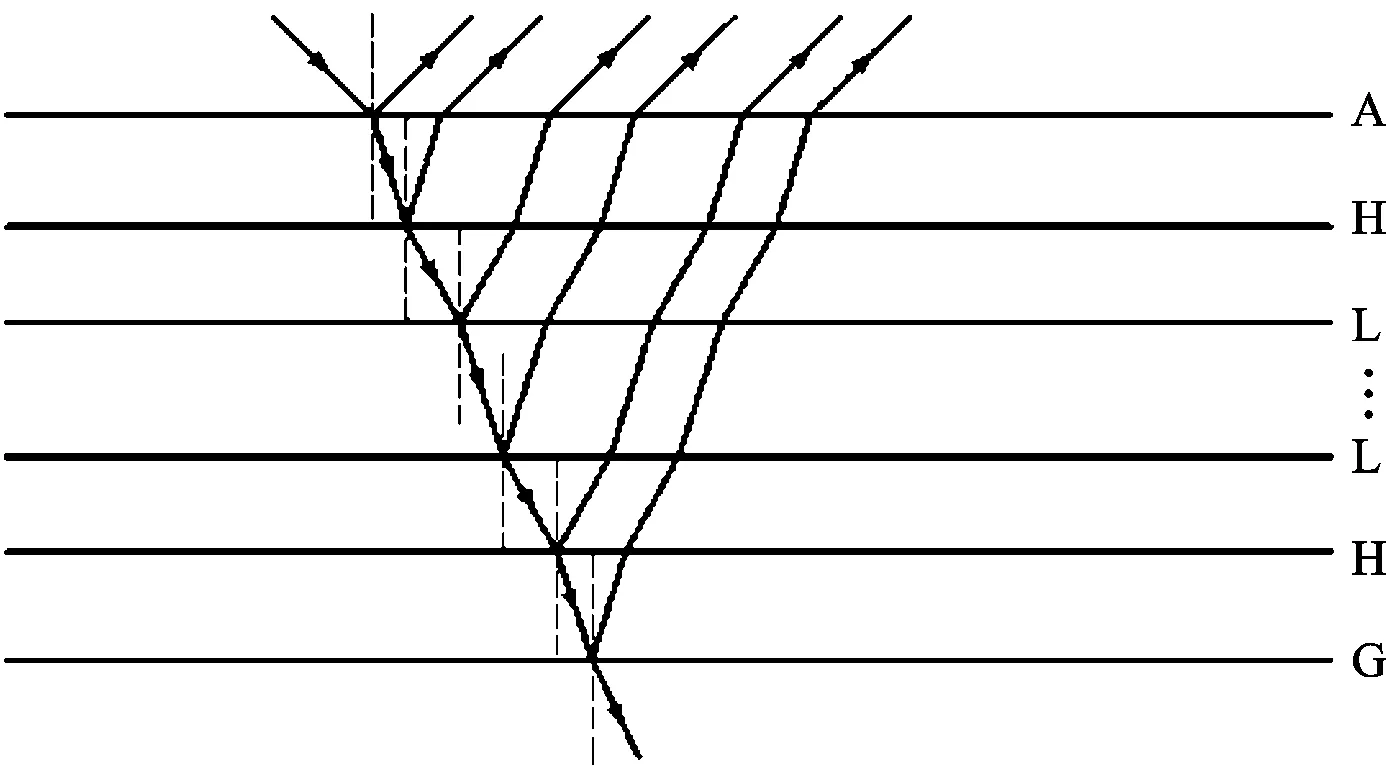
图3 高反镜反射模型

2.2 高反镜入射角误差对滚转角测量的影响

高反镜各个膜层厚度是按照45°角入射设计的,在实际操作中保证入射角为严格45°是比较困难的,当入射角存在误差时,光在各膜层的折射角变化导致光程差变化,使高反镜反射光的p分量与s分量都发生变化。

计算边界上场量之间的线性关系[10],s分量的表达矩阵为

(4)

式中:EI和HI分别为空气介质中通过界面上一点沿固定方向传播的电场波和磁场波的总和;EN和HN分别为基底介质中通过界面上一点沿固定方向传播的电场波和磁场波的总和;H为高折射率材料的特征矩阵;L代表低折射率材料的特征矩阵。

由式(4)整理得s分量的反射系数为

(5)

式中:pN为入射角和基底材料K9折射率nG的函数;p1为入射角和空气折射率nA的函数。

以二氧化钛作为高折射率材料、二氧化硅作为低折射率材料,将折射率nG=1.516 3、nA=1、nH=2.34、nL=1.457以及T=10代入式(5),取r(s)的幅值和相位,可得rs、δs与高反镜入射角o的关系如图4a、4b所示。同理,可得rp、δp与高反镜入射角o的关系,如图4c、4d所示。

假设高反镜1的入射角为o1、高反镜2的入射角为o2,由于两高反镜互相垂直,有o1+o2=90°,如图5所示。

两高反镜入射角分别为o1和90°-o1时的琼斯矩阵元素rjp、rjs、δjp和δjs可在图4中得出,将此时的琼斯矩阵M1、M2代入式(1),当1/4波片夹角θ=2°时,得到参考信号与测量信号的相位差ψ,求导并取最大值得到系统放大倍数与高反镜1入射角o1的关系如图6所示。由图6可知,曲线以o1=45°左右对称,当o1取36°或54°时,放大倍数取得最大值720倍。

2.3 高反镜反射率

高反镜的反射率较低会导致信号的信噪比降低,增大测量结果的不确定度,因此有必要对两高反镜的反射率进行计算。当偏振光入射时,反射比R与s分量和p分量的反射比Rs、Rp有以下关系[11]

R=Rssin2γ+Rpcos2γ

(6)

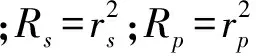
(a)rs与o的关系

(b)δs与o的关系

(c)rp与o的关系

(d)δp与o的关系图4 rs、δs、rp和δp与高反镜入射角o的关系图

图5 高反镜1、高反镜2的入射角

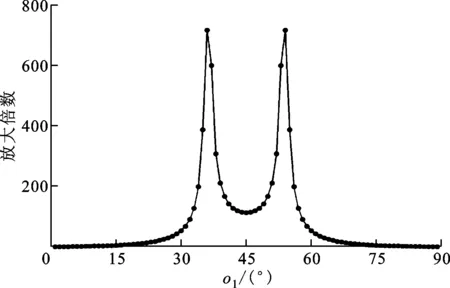
图6 系统放大倍数与高反镜1入射角o1的关系图

图7 不同入射角下高反镜反射比与入射波方位角的关系图

3 实验验证

图8 实验平台

基于上述分析,搭建如图8所示的实验平台进行实验验证。所用光源为双频激光器,频差为730 kHz,两高反镜固定在分辨率为0.1°、转动轴平行于x轴的精密转台上,通过转动转台可调节高反镜入射角大小。1/2波片固定在精密波片架上,其转动模拟导轨滚转角变化,波片架转动分辨率为1.7′。实验时调节θ=2°,用CH6000A相位计观察参考信号与测量信号的相位差ψ,相位计分辨率为0.01°。由于当高反镜1入射角o1=36°时,滚转角α在灵敏区内的光强较小,相位计接收的测量信号不稳定,故调节转台使o1=38°。转动1/2波片直到最大的放大倍数出现,其局部相位差ψ与滚转角α的关系如图9所示,线性拟合得到系统放大倍数可达到346倍,与理论分析结果相吻合,此时系统测量分辨率可达0.1″。此实验验证了高反镜入射角误差对滚转角测量影响的理论分析,而且提供了一种通过改变高反镜入射角来增大滚转角测量精度的思路。

图9 实验测得相位差ψ与滚转角α的关系图

4 结 论

本文主要分析了高反镜入射角误差对反射光的影响,进而造成对滚转角测量系统测量灵敏度的影响,并进行了实验验证。结果表明:测量系统的放大倍数随高反镜入射角不同而变化,并在入射角为36°时取得最大值720倍,达到高反镜正常角度入射时放大倍数的6倍;实验验证当高反镜入射角为38°时,系统放大倍数达到346倍,采用分辨率为0.01°的相位计,滚转角的测量分辨率可达0.1″,提供了一种通过改变高反镜入射角来增大滚转角测量精度的思路。

[1] 侯文玫, 钟朝阳, 乐燕芬, 等. 高精密滚转角测量干涉仪 [J]. 机械工程学报, 2014, 50(22): 22-27. HOU Wenmei, ZHONG Chaoyao, LE Yanfen, et al. High precision roll angle interferometer [J]. Journal of Mechanical Engineering, 2013, 47(5): 99-103.

[2] 陶卫, 浦昭邦. 光栅楔形平板及其在转角测量中的应用 [J]. 光电子·激光, 2002, 13(4): 371-374. TAO Wei, PU Zhaobang. Grating wedge disk and its application in the measurement of rotating angle [J].

Journal of Optoelectronics: Laser, 2002, 13(4): 371-374.

[3] 钟丽红, 王昭, 汤善治, 等. 机床滚转角测量中敏感元件倾斜引起的误差分析 [J]. 西安交通大学报, 2013, 47(5): 99-103. ZHONG Lihong, WANG Zhao, TANG Shanzhi, et al. Measurement error analysis for machine tool error measurement due to inclined half wave plate [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 99-103.

[4] TANG Shanzhi, WANG Zhao, GAO Jianmin, et al. Measurement method for roll angular displacement with a high resolution by using diffraction gratings and a heterodyne interferometer [J]. Review of Scientific Instruments, 2014, 85: 045110.

[5] JIANG H, YIN C. Sensitivity enhanced roll angle measurement [J]. Opt Eng, 2000, 39(2): 516-519.

[6] WU Chien-ming, CHANG Yi-tsung. Roll angle displacement system with microradian accuracy [J]. Sensors and Actuators: A, 2004, 116: 145-149.

[7] LIU Zhongyao, LIN Dejiao, JIANG Hong, et al. Roll angle interferometer by means of wave plates [J]. Sensors and Actuators: A, 2003, 104: 127-131.

[8] 李朝辉, 王昭, 黄军辉, 等. 滚转角测量中直角棱镜相位损失及解决方法 [J]. 西安交通大学学报, 2014, 48(9): 112-116. LI Zhaohui, WANG Zhao, HUANG Junhui, et al. Phase loss of right-angle prism in roll angle measurement and its solution [J]. Journal of Xi’an Jiaotong University, 2014, 48(9): 112-116.

[9] 李朝辉, 王昭, 黄军辉, 等. 直角棱镜的保偏反射膜设计及分析 [J]. 中国激光, 2015, 42(3): 1-5. LI Zhaohui, WANG Zhao, HUANG Junhui, et al. Design and analysis of the polarization-preserving films for rectangular prism [J]. Chinese Journal of Lasers, 2015, 42(3): 1-5.

[10]唐晋发, 顾培夫, 刘旭, 等. 现代光学薄膜技术 [M]. 杭州: 浙江大学出版社, 2006: 107.

[11]郁道银, 谈恒英. 工程光学基础教程 [M]. 北京: 机械工业出版社, 2007: 193.

(编辑 荆树蓉)

Error Analysis on the Roll Angle Measurement of Machine Tool’s Guideway

QI Jingya1,WANG Zhao1,HUANG Junhui1,YU Bao1,GAO Jianmin2

(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. State Key Laboratory for Manufacturing System Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To evaluate the influence of incident angle error of the reflector on the roll angle measurement of machine tool’s guideway, a new mathematical model was established by Jones matrix method. The new model takes the influence of the incident angle error of high-reflectivity mirror into consideration based on the existing model. The reflected light of the mirror with different incident angles was analyzed based on the action mechanism of multiple dielectric films. Then the influence of incident angle error of reflector on the roll angle measurement was calculated. Results showed that the measurement gain coefficient varied with the incident angle and a maximum value of 720 was obtained when the incident angle was 36-deg, a 6-fold increase compared with previous results. In the experimental setup, we measured a gain coefficient of 346 at the 38-deg incident angle to the mirror. A roll angle measuring resolution 0.1-arcsec was attained using a phase meter with a resolution of 0.01-deg. The theoretical analysis of the new model was verified, which also provides a measuring sensitivity enhancement approach by carefully controlling the incident angle of the mirror.

roll angle; high-reflectivity mirror; incident angle; measuring sensitivity; machine tool’s guideway

2016-02-24。 作者简介:齐静雅(1991—),女,博士生;黄军辉(通信作者),男,讲师。 基金项目:国家自然科学基金资助项目(61405156)。

时间:2016-06-08

10.7652/xjtuxb201609005

TH741

A

0253-987X(2016)09-0031-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160608.1034.002.html