包含函数Γ(x)的对数完全单调函数及不等式
2016-12-21李晶晶孙梅
李晶晶,孙梅
(西北大学数学学院,陕西西安710127)
包含函数Γ(x)的对数完全单调函数及不等式
李晶晶,孙梅
(西北大学数学学院,陕西西安710127)
基于欧拉Gamma函数的奇特性质,利用函数的单调性理论以及一些简单函数的积分表达式与级数展开式证明了函数fα(x),α∈R和函数s(x)的对数完全单调性,并利用该性质得出了一个比原有结论更精确的不等式以及一个双边不等式.
完全单调性;对数完全单调性;Gamma函数;充分条件
1 引言
欧拉Gamma函数是一种非常重要的特殊函数,在数学的许多分支以及物理,工程等学科中都有着十分重要的重要作用.欧拉Gamma函数定义为:
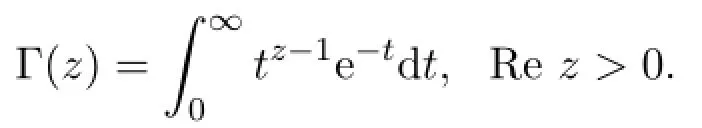
函数

作为函数Γ(z)的对数的导数,被称为digamma函数.对于i∈{0}∪N,导函数ψ(i)(z)被称为polygamma函数,其中N表示所有正整数的集合.特殊地,函数ψ′(z)和ψ′′(z)被称为trigamma函数和tetragamma函数.
称函数f在区间I上完全单调,如果f在区间I上存在各阶导数且满足:
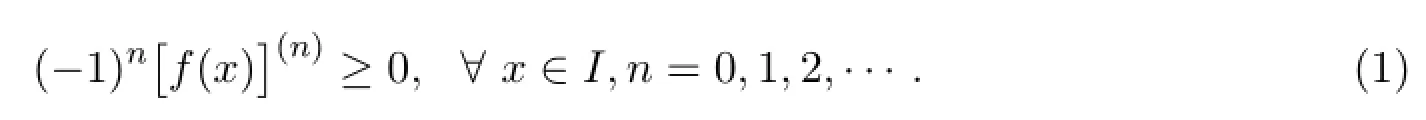
如果不等式(1)严格成立,则称函数f在区间I上严格完全单调[1-4].
称函数f在区间I上对数完全单调,如果它的对数lnf在区间I上存在各阶导数且满足:
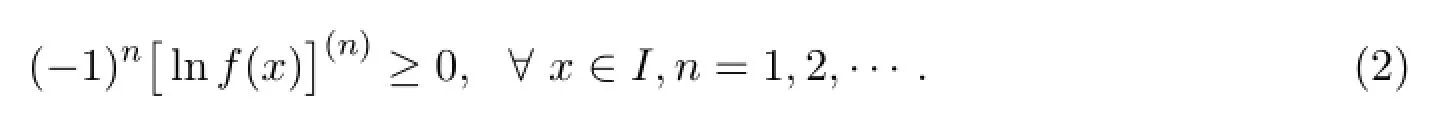
如果不等式(2)严格成立,则称函数f在区间I上严格对数完全单调[1-4].
2 引理
为了证明主要结论,先给出下面的引理.

3 主要结论






4 结束语
本文利用函数的单调性理论,指数函数的级数展开式以及一些简单函数的积分表达式证明了函数fα(x),α∈R和函数s(x)的对数完全单调性,利用该性质,由定理3.1和定理3.2分别得出比(10)式更加精确的不等式(9)和一个双边不等式.通过查阅资料,还了解到q-gamma函数的一些相关概念及其与Gamma函数的关系,在今后的工作中可以考虑研究其完全单调单调性,并得出一些很好的结论.
[1]Guo S.Some classes of completely monotonic functions involving the gamma function[J].J.Pure Appl. Math.,2006,30(4):561-566.
[2]Mitrinović D S,Pečarić J E,Fink A M.Classical and New Inequalities in Analysis[M].London:Kluwer Academic Publishers,1993.
[3]Schillin R L,Song R,Vondrač Z.Bernstein Functions:Theory and Applications.de Gruyter Studies in Mathematics 37[M].2nd ed.Berlin:Walter de Gruyter,2012.
[4]Widder D V.The Laplace Transform[M].Princeton:Princeton University Press,1946.
[5]Chen Chaoping,Qi Fen.Completely monotonic function associated with the Gamma functions and proof of Wallis’inequality[J].Tamkang Journal of Mathematics,2005,36(4):303-307.
[6]Chen Chao ping.Complete monotonicity and logarithmically complete monotonicity properties for the gamma and psi functions[J].Mathematical Analysis and Applications,2007,336(2):812-822.
[7]Qi Feng,Guo Baini,Chen Chaoping.Some completely monotonic functions involving the gamma and polygamma functions[J].Aust.Math.Soc.,2006,80(1):81-88.
[8]Qi Feng,Chen Chaoping.A complete monotonicity property of the gamma function[J].Journal of Mathematical Analysis and Applications,2004,296(2):603-607.
Logarithmically completely monotonic functions and inequalities involving the function Γ(x)
Li Jingjing,Sun Mei
(College of Mathematics,Northwest University,Xi′an710127,China)
Based on unique properties of the gamma function,this paper proves the logarithmically complete monotonicities of the function fα(x),α∈R and the function s(x)by the monotonicity theory,the integral representations and the series expansions of some simple functions.Using the property,it concludes a inequalities that is more accurate than the original conclusion and a two-side inequality.
completely monotonicity,logarithmically completely monotonicity,Gamma function,sufficient condition
O174.6
A
1008-5513(2016)02-0182-08
10.3969/j.issn.1008-5513.2016.02.009
2015-12-10.
陕西省自然科学基金(2010JM1017).
李晶晶(1989-),硕士生,研究方向:特殊函数论.
2010 MSC:33B15
