推理“三助手”

●黄琴 张兴筑

推理“三助手”

●黄琴 张兴筑

不断提出问题是学生数学思维发展的必经过程，数学学习就是在问题的驱动下，利用图形和符号不断进行推理的过程，问题、图形和符号与推理密不可分。

一、创设问题情境，使推理有根据

问题情境的创设可以激发学生的深入思考，使学生的思维活动向着纵深方向发展。

执教人教版《数学》九年级上册《一元二次方程根与系数的关系》的巩固训练环节，笔者出示思考题：设x1、x2是一元二次方程2x2+3x-1=0的两个根，求代数式的值。刚开始学生的普遍做法是：先解一元二次方程2x2+3x-1=0，求得，再把x1、x2的值代入原式求值。计算过程比较麻烦。这时有一位学生提出：“老师，这道题有没有其他简便的方法？”笔者借机让学生仔细观察原式，找出特点。学生思考后发现原式能化成，只要能求出x1+x2和 x1x2的值，就可以求出原式的值。x1+x2和x1x2的值又是多少呢？这就巧妙地联系了这节课的重点教学环节：一元二次方程根与系数关系的求解。根据之前的学习经验，结合题设，学生很容易求出x1+x2和x1x2的值，再将数值代入转化后的代数式即可得解。

以上教学中，教师设计一系列的数学问题，通过观察、发现、猜想、验证等思维活动，让学生自己去思考、探究，巧妙运用已学知识“一元二次方程根与系数关系”得出问题解决的简便路径。。

二、巧用图形，使推理更直观

图形直观形象，而且根据图形能提炼出很多有价值的东西。教学过程中，教师巧妙地运用图形，可以使学生的思路更清晰、推理更直观。

执教人教版《数学》九年级上册《实际问题与一元二次方程》的导入环节，笔者出示思考题：某县实验中学有一个长30米，宽20米的矩形绿地，扩建校园时，准备把绿地的长、宽各增加x米。设增加的面积为y平方米，求出y与x之间的函数关系式。刚开始学生没有画图，用的是代数加减法，因为增加的面积＝新矩形的面积－原矩形的面积，所以y＝(x+ 30)(x+20)-30×20=x2+50x。笔者在肯定学生的算法后，在黑板上画出如下图所示图形，让学生运用几何割补法推导出图中阴影部分的面积。学生的思路顿时被打开了。有的说：连接CE、CM和CP。因为S阴影=SΔCBE+SΔCEM+SΔCMP+SΔDCP，所以。有的说，延长BC交PM于点N。因为S阴影=S矩形BEMN+S矩形DCNP,所以S阴影=x(x+20)+30x=x2+50x。有的说：延长DC交EM于点F。因为S阴影=S矩形PDFM+S矩形CBEF，所以S阴影=x(x+30)+20x= x2+50x。还有的说：连接CM，因为S阴影=S梯形CBEM+S梯形PDCM，所以。

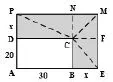
从上例可以看出，在没有图形的背景下，学生的思维难于打开，推理方法单一；有了图形，学生可以进行多重推理。

三、借助符号，使推理更简捷

符号可以简约有效地表示数、数量关系及其变化规律。借助符号，能使推理更加简便快捷。

同样是执教《实际问题与一元二次方程》，在巩固训练环节，笔者出示思考题：甲、乙两人同时在同一粮店购买粮食两次（假设两次购买粮食的单价不同），甲每次购买粮食100千克，乙每次购买粮食用去100元。若规定谁两次购买粮食的平均单价低，谁的购粮方式就合算。据此推断甲、乙两人的购粮方式中哪一个更合算？这道推理题，光靠文字语言，很难把道理说清楚，因为两次购买粮食的单价都不知道。此处需要借助符号语言，将两次购买粮食的单价分别用不同的字母来表示，再进行推理就容易很多。具体来说，可设甲、乙两人第一次购买粮食的单价为x元/千克，第二次购买粮食的单价为y元/千克，再设甲两次购买粮食的平均单价为M元/千克,乙两次购买粮食的平均单价为N元/千克。则，所以。因为x＞0，y＞0且 x≠y，所以M-N＞0，M＞N。由此推断出乙的购粮方式更合算。

推理贯穿于数学学习的始终，推理能力的形成和提升需要一个长期的、循序渐进的过程。教学中教师要引导学生抓住问题、图形和符号等影响推理的关键因素，逐步增强学生们问题意识、数形结合意识和符号意识。

（作者单位：房县实验中学）