一热孔弹塑性完全耦合作用下的井底岩石应力分布

祝效华, 刘伟吉

(西南石油大学机电工程学院,四川成都 610500)



一热孔弹塑性完全耦合作用下的井底岩石应力分布

祝效华, 刘伟吉

(西南石油大学机电工程学院,四川成都 610500)

井底待破碎岩石所处的应力状态作为影响其破碎的关键因素而直接影响着钻井效率,建立综合考虑上覆岩层压力、水平地应力、液柱压力以及孔隙压力和地层温差完全耦合作用下井底岩石的三维物理模型,借助有限元软件进行求解,研究在不同液柱压力、不同井深、不同温差以及不同渗透系数作用下井底岩石应力分布的数值解。结果表明:液柱压力、井深以及温差越大,井底表面岩石最大主应力越大;渗透系数减小,井底表面最大主应力先增大后减小;在井眼轴向方向,在距离井底表面以下一定距离之后,液柱压力和井深越大,岩石最大主应力越小;温差对岩石最大主应力没有影响。

热孔弹塑性; 井底应力; 完全耦合; 数值解; 破碎机制

随着勘探开发不断向深部地层发展,岩石的可钻性越来越差,机械钻速也大幅度下降[1]。井底待破碎岩石所处的应力状态作为影响其破碎的关键因素而直接影响着钻井效率,因此研究井底应力分布情况对于正确认识井底岩石破碎机制和提高钻井效率有重要作用。近年来,针对井底应力分布的研究较多,并且也得出了一些有用的结论[2-15];但是针对热孔弹塑性完全耦合作用下井底岩石应力分布的研究还较少。研究热孔弹塑性完全耦合作用下井底岩石应力的分布情况更符合实际的井底工况,对于正确认识井底岩石破碎机制和提高钻井效率很有必要。笔者建立综合考虑上覆岩层压力、水平地应力、液柱压力以及孔隙压力和地层温差完全耦合作用下井底岩石的三维物理模型,借助有限元软件进行求解,研究井底岩石应力分布情况。

1 热孔弹性理论

地层温度随地层深度的增加而增加,钻井液从地面到井底的过程中温度不断升高,但还是低于地层温度,因此对井底有冷却作用,井底岩石骨架和孔隙介质都会收缩;如果液柱压力和孔隙压力存在差值,在井底会发生钻井液和孔隙流体的相互渗透。钻井液与地层的传热和渗透过程示意图如图1所示。

假设:孔隙流体流动满足Darcy定律;孔隙流体充满整个孔隙,流体不可压缩,不考虑相变的影响;耦合方程组中的能量方程以热传导方程为基础,考虑了饱和介质的热传导作用,岩石与流体的热交换假定为瞬时完成;液体黏度不随温度变化,岩石密度和流体密度也不随温度变化,岩石的孔隙度与岩石渗透率是常数,不随岩石骨架应力变化而变化。

热孔弹性完全耦合作用下的控制方程组为

其中

ρscs=(1-n)ρmcm+nρfcf, ks=(1-n)km+nkf.

式中,p为孔隙压力,MPa;T为温度,℃;α为Biot系数;Km为岩石骨架体积模量;Kf为孔隙流体和体积模量,MPa;ks、kf和km分别为岩石、孔隙流体和岩石骨架的热传导系数,J/(m·s·℃);fj为体积力;k为岩石渗透率,m2;μ为流体黏滞系数,Pa·s;cm和cf分别为岩石骨架和流体的比热容,J/(g·℃);ρm和ρf分别为岩石骨架和流体的密度,kg/m3;εv为体积应变;n为岩石孔隙度;βs、βm和βf分别为饱和岩石、岩石骨架和流体的热膨胀系数,℃-1;λ和G为与弹性模量相关的常数;v为Darcy流速。

2 岩石塑性屈服准则

岩土材料采用Drucker-Prager塑性准则,将偏应力视为材料破坏原因,同时反映了体积应力对材料强度的影响。根据Drucker-Prager强度准则,认为中间主应力对岩土的破坏有影响,克服了Mohr-Coulomb准则的不足[16-18]:

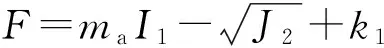
其中

I1=σ1+σ2+σ3,

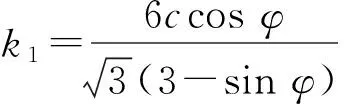
式中,I1和J2分别为第一应力不变量和应力偏量第二不变量;φ为内摩擦角; c为内聚力;σ1、σ2和σ3分别为柱坐标系下的3个主应力。

3 有限元模型的建立与验证

3.1 有限元模型的建立

建立热孔弹塑性完全耦合作用下井底岩石的三维物理模型,模型为边长2 m的正方体,井眼半径为108 mm,深度为1 m,模型示意图如图2所示。模型包含14 403个热孔完全耦合作用的三维实体单元,每个单元有8个节点,计算的基本变量有位移、温度和孔压,单元内部各点的位移、温度和孔压通过一阶差值方式间接得到。在井眼轴线方向岩石受上覆岩层压力σz的作用;在径向方向受最大主应力σH和最小主应力σh的作用,在本文计算中两个水平主应力相等,由侧压系数和上覆岩层压力计算可得;井底和井壁受液柱压力pw作用,井底岩石三维模型在z方向有位移约束;岩石内部有孔隙压力pf;除此之外,由于在井底钻井液与地层初始温度有差异,存在一定的温差,假设地层的温度梯度为3 ℃/100 m;井壁为渗透边界,井筒内的钻井液和地层孔隙流体可以自由流通,也就是说井壁处的孔隙压力和钻井液液柱压力相等;由于钻头破碎岩石形成新井底的过程很快,所以井筒内钻井液和井底岩石孔隙流体发生流通的时间很短暂,假设为5 s。为了方便,取轴向路径和径向路径进行分析,如图2中红色线条所示。

图2 井底岩石受力示意图

其中,岩土材料的物理参数如下:弹性模量E为25 406 MPa;泊松比u为0.302;拉梅常数λ为14 806.4 MPa;渗透系数K为1×10-10m·s-1;孔隙度n为0.1;岩石密度ρm为2 500 kg/m3;岩石骨架热膨胀系数βm为1.5×10-5℃-1;岩石骨架热传导系数km为3.08 J/(m·s·℃);岩石骨架比热容cm为896 J/(g·℃);Biot系数α为1;孔隙流体热传导系数kf为0.58 J/(m·s·℃);孔隙流体比热容cf为4 200 J/(g·℃);孔隙流体热膨胀系数βf为2×10-4℃-1;孔隙流体密度ρf为1 000 kg/m3;流体比重γw为1×104N/m3;流体黏滞系数μ为0.001 Pa·s;剪切模量G为9 756 MPa;内聚力c为26.13 MPa;摩擦角φ为24.47°。

3.2 有限元模型的验证

根据线性孔隙弹性理论,在井壁可渗透的情况下,可求得井眼计算模型中距井眼轴线r处的有效应力为

ξ=α(1-2u)(1-u).

式中,σr、σθ和σz分别为径向、周向和轴向的有效应力;σH和σh分别为最大水平主应力和最小水平主应力;δ为与渗透性有关的系数,当井壁有渗流时为1,无渗流时为0;p(r)为距井壁r处的孔隙压力;pw为液柱压力;pp为初始孔隙压力;ri为井眼半径。

为了验证所建有限元模型的正确性,在不考虑温度影响的情况下对通过数值仿真得出的结果和解析方法得出的结果进行对比,在距井底0.8 m处井壁的径向应力和周向应力的数值解和解析解如图3所示。由图3可知,两者的计算结果相似度很高,验证了该数值计算模型的正确性,在该模型的基础上加上地层的初始温度和钻井液的温度,然后使用该方法继续对相关问题进行研究。

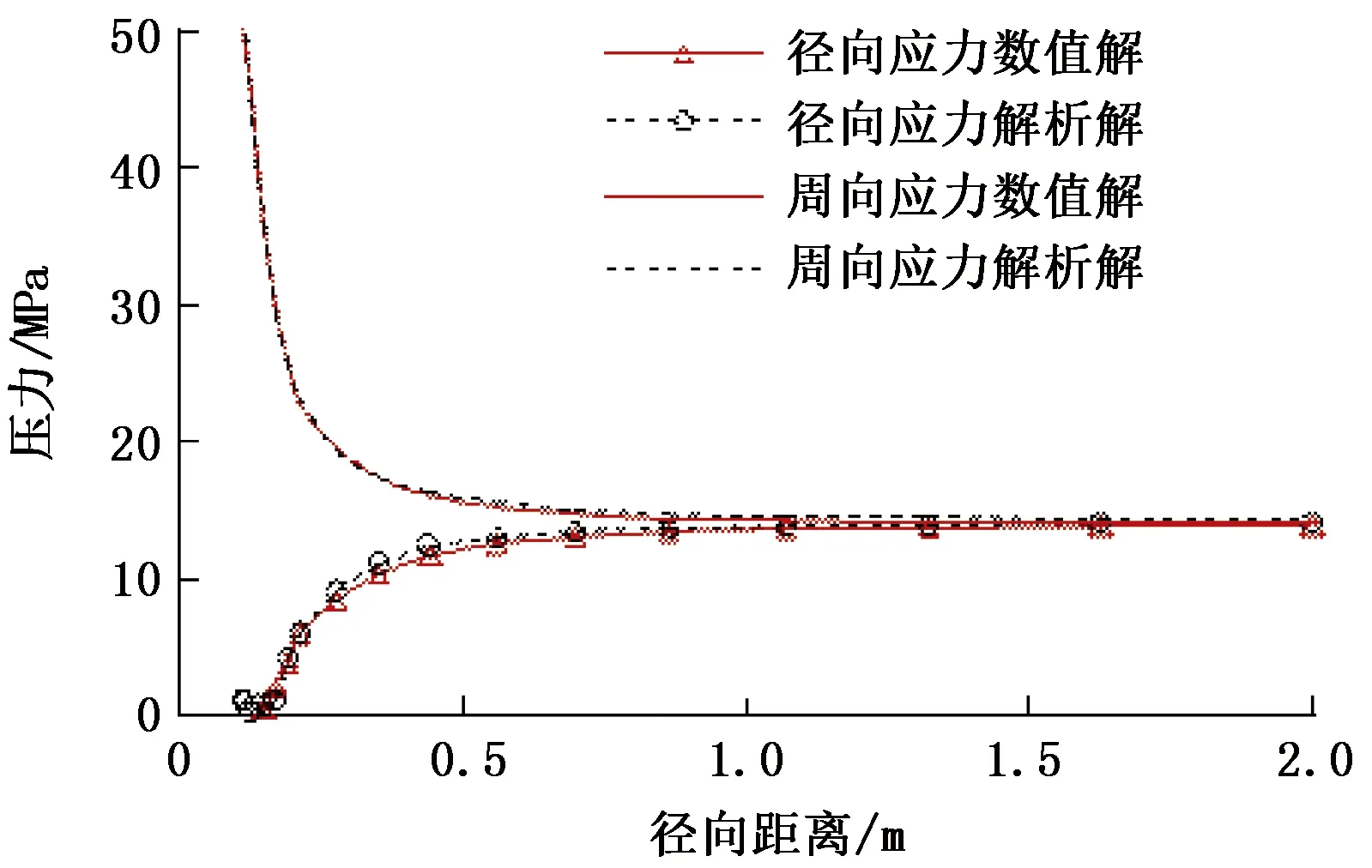
图3 数值解和解析解对比

4 结果分析

4.1 孔隙压力和温度分布

由于钻头破碎岩石形成新井底的过程很快,所以井筒内钻井液和井底岩石孔隙流体发生流通的时间很短暂,假设为5 s。岩土材料的各项物理参数如上述所示,钻井液压力为20 MPa,上覆岩层压力为75 MPa,钻井液温度为60 ℃,地层初始温度为90 ℃。井壁和井底周围孔隙压力和温度的分布如图4所示。由图4可知,井壁处的孔隙压力和温度分别为20 MPa和60 ℃,与模型中施加的孔隙压力边界和温度边界相等。

图4 孔隙压力和温度分布

4.2 液柱压力对井底应力的影响

钻头破岩形成井眼之后,钻井液液柱压力代替所破碎的岩石对井底表面起压持作用。钻井液会与地层孔隙流体发生渗流并且渗流过程与时间有关,从而影响井底周围的孔隙压力;并且钻井液温度和初始地层温度存在差别,会发生热传导效应,对于下部地层钻井液温度一般低于地层温度,温度的变化也影响井底周围孔隙压力的变化。本文中地层初始温度为90 ℃、钻井液温度为60 ℃,井眼半径为108 mm,上覆岩层压力为75 MPa,上覆岩层压力由岩石密度和井深计算得到。

井底岩石受到上覆岩层压力、水平地应力、液柱压力、孔隙压力以及温差等因素的综合影响,其应力情况变现得非常复杂。井底岩石在不同液柱压力作用下的应力分布如图5所示。由图5(a)可知,随着液柱压力的增大井底岩石表面最大主应力增大,远离井眼轴线岩石应力减小,在井底面与井壁的交界处最小,并且呈现出压应力;井底面最小主应力分布如图5(a)中虚线所示,气体钻井中,井底岩石中心部分都表现为拉应力,其他部分为压应力;随着液柱压力的增大拉应力区域变小,压应力区变大,最后井底岩石最小主应力都呈现出压应力。由此可见,井底待破碎岩石按照应力状态分为3个区域,分别为三向拉伸区(有时为单向压缩区,位于井眼中部)、两向压缩区(位于井眼中部靠井壁一侧)和三向压缩区(位于井底面与井壁交界处);由此对应的破碎难易程度为极易破碎区、易破碎区和难破碎区,应该采取相关的应对措施。

图5(b)为井眼轴向方向上井底岩石最大主应力分布。由图5(b)可知,液柱压力越大,井底岩石表面最大主应力也就越大,随着远离井底表面这种规律发生变化;当距井底表面一定距离后(本文中计算值为20 mm),液柱压力越小其对应的岩石最大主应力越大。出现上述现象的主要原因是井底表面孔隙压力的影响,在高渗透地层,由于井底表面可以看作是自由流通的面,井底表面的孔隙压力随着液柱压力的增大而增大,而井底岩石骨架承受的压应力随着孔隙压力的减小而增大,岩石骨架承受的拉应力随着孔隙压力的增大而增大,所以孔隙压力的增大有利于井底岩石的破碎,但井底孔隙压力增大的同时液柱压力也随之增大,使井底岩石强度和塑性都增大,并且液柱压力的增大使钻井液对井底岩石的压持力增大,这些因素都制约着井底岩石的高效破碎。在井底面与井壁交界处的岩石最不容易被破碎,应该采取相应的措施。在气体钻井中,井底岩石在轴向方向的最大主应力呈先增大后减小的趋势,最大主应力在井底面为5.17 MPa,在距井底表面40 mm处出现最大值11.5 MPa;而在钻井液钻井中,井底岩石在轴向方向所受的最大主应力呈下降趋势。

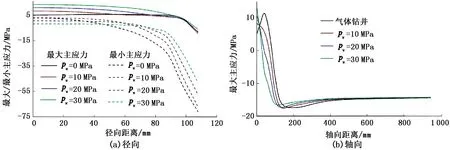
图5 不同液柱压力下井底面径向和轴向方向最大/小主应力分布

4.3 地层深度对井底应力的影响

不同地层深度下井底最大、最小主应力分布如图6所示,压差为10 MPa,温差为30 ℃。随着井深的增加,井底面最大主应力增大,这主要是由于随着井深的增加,在钻井液密度不变的情况下井底处的液柱压力增加,使井底表面孔隙压力增大,岩石骨架承受的拉应力增大,如图6(a)中实线所示。最小主应力在井眼中心地带基本不变,在靠近井壁处随井深的增加压应力增加,且井深越深压应力越大,如图6(a)中虚线所示。由图6(b)可知,最大主应力在轴向方向呈下降趋势,最后稳定在某个值,并且在距井底表面以下一定距离之后,井深越小对应的岩石最大主应力反而越大。

不同井深情况下(以气体钻井为例,温差为30 ℃)井底岩石沿井眼轴线方向最大主应力分布如图7所示。在气体钻井中井筒内的压力约为0 MPa,井底面和井壁的孔压边界条件也为0 MPa。由图7可知,随着井深的增加最大主应力沿轴向方向的变化从逐渐减小到稳定(1 km井深),变化状态为先增大后减小再稳定(2、3、4 km井深);随着井深的增加井底表面的最大主应力变化不大,在井底表面以下一定距离范围内的岩石最大主应力随着井深的增大而增大。

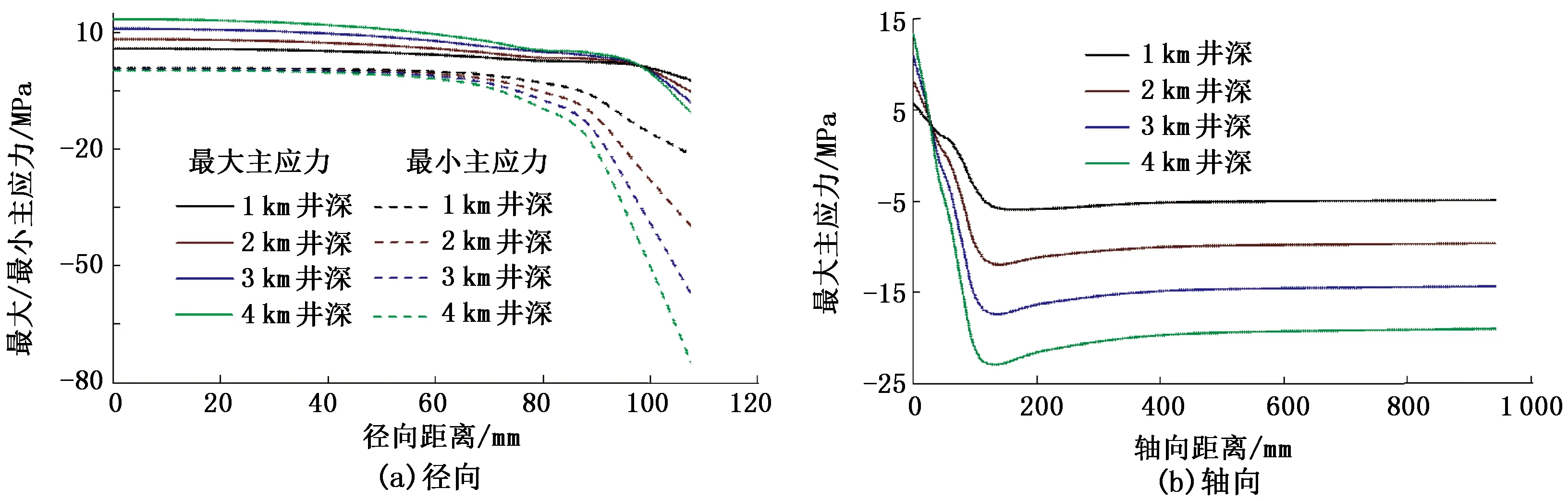
图6 不同井深下径向和轴向方向最大/小主应力分布

图7 不同井深下沿轴向方向井底岩石最大主应力分布

4.4 不同温差对井底应力的影响

钻井液从地面流入到井底的过程中,其温度随地层温度的升高而升高,但仍低于地层温度,二者间存在温差。不同温差下最大主应力的分布如图8所示。由图8可知,温差越大井底最大主应力越大,有利于井底岩石的破碎;温差对井底岩石应力的影响只表现在距离井底表面以下一定距离范围内的岩石,这与岩石骨架、孔隙流体的热传导系数以及热传导时间等因素有关。

图8 不同温差下井底径向和轴向方向最大主应力分布

4.5 渗透系数对井底应力的影响

渗透系数是指孔隙流体通过孔隙骨架的难易程度。在气体钻井中,当温差为30 ℃时,不同渗透系数下井底表面和井底岩石沿径向和轴向方向上的最大主应力分布如图9所示。由图9可知,随着渗透系数减小,井底表面岩石最大主应力先增大后减小,渗透系数1×10-7mm/s为转折点;在井眼轴向方向,随着渗透系数减小,井底岩石最大主应力先增大后减小。

图9 不同渗透系数下井底径向和轴向方向最大主应力分布

5 结 论

(1)在渗透地层,井底表面岩石的孔隙压力和井筒内液柱压力相同,并且随着时间的推移液柱压力的影响越来越广;孔隙压力的增大使岩石骨架应力减小对岩石破碎有利,孔隙压力减小使岩石骨架应力增大对破岩不利;当液柱压力变大时,井底岩石表面最大主应力变大,虽然有利于岩石破碎,但是液柱压力变大使岩石强度和塑性以及对岩屑的压持力都增大,不利于岩石破碎;在液柱压力小的情况下(以气体钻井为例),虽然在井底表面最大主应力要小于有液柱压力的情况,但是在距井底表面以下一定距离之后其最大主应力明显大于有液柱压力的情况,并且岩石强度和压持力较小,脆性较大,对于井底岩石的大块破碎有利。

(2)井底待破碎岩石按照应力状态分为三向拉伸区(有时为单向压缩区,位于井眼中部)、两向压缩区(位于井眼中部靠井壁一侧)和三向压缩区(位于井底面与井壁交界处周围),由此对应的破碎程度为极易破碎区、易破碎区和难破碎区。

(3)在相同压差的情况下,井深越大井底表面岩石最大主应力越大;在井眼轴向方向上,在距离井底表面以下一定距离后,井深越大对应的岩石最大主应力反而越小。在相同液柱压力下(以气体钻井为例),随着井深的增加,最大主应力沿轴向方向的变化为先增大后减小再稳定;并且随着井深的增加井底表面的最大主应力变化不大,但在井底表面以下一定范围内的岩石最大主应力变大,并且表现为拉应力。

(4)温差越大井底表面最大主应力越大,有利于井底岩石的破碎,温差对井底岩石应力的影响只表现在距离井底表面以下一定距离范围内的岩石,这与岩石骨架、孔隙流体的热传导系数以及热传导时间等因素有关;井底岩石最大主应力随着渗透系数的减小呈先增大后减小的趋势,渗透系数存在一个临界值。

[1] 李根生,史怀忠,沈忠厚,等.水力脉冲空化射流钻井机制与试验[J].石油勘探与开发,2008,35(2):239-243. LI Gengsheng, SHI Huaizhong, SHEN Zhoughou, et al. Mechanisms and tests for hydraulic pulsed cavitating jet assisted drilling[J]. Petroleum Exploration and Development, 2008,35(2):239-243.

[2] RUMZAN I, SCHMITT D R. The influence of well bore fluid pressure on drilling penetration rates and stress dependent strength[J]. Rock Mechanics in the National Interest, 2001,1:911-917.

[3] 彭烨,沈忠厚,樊胜华.基于开挖方法的井底应力场有限元模型[J].石油学报,2006,27(6):133-136. PENG Ye, SHEN Zhoughou, FAN Shenghua. Finite element model for analyzing stress field of bottom hole based on excavating method[J]. Acta Petrolei Sinica, 2006,27(6):133-136.

[4] 林铁军,练章华,刘健,等.空气钻井井斜问题与地层倾角的规律探讨[J].钻采工艺,2007,30(3):7-9. LIN Tiejun, LIAN Zhanghua, LIU Jian, et al. Discussion on the rule of well deviation and tratigraphic dip in air drilling[J]. Drilling & Production Technology, 2007,30(3):7-9.

[5] 王敏生,唐波.井底应力场对气体钻井井斜的影响[J].岩土力学,2009,30(8):2436-2441. WANG Minsheng, TANG Bo. Effects of stress field in bottom hole on borehole deviation during gas drilling[J]. Rock and Soil Mechanics,2009,30(8):2436-2441.

[6] 朱化蜀,余瑞青,王滚,等.气体钻井地层剪切应力井斜规律研究[J].天然气技术与经济,2011,5(1):28-30. ZHU Huashu, YU Ruiqing, WANG Gun, et al. Law of well deviation caused by formation shear stress in gas drilling[J]. Natural Gas Technology and Economy, 2011,5(1):28-30.

[7] 朱化蜀,余瑞青,廖忠会,等.气体钻井井斜有限元岩石应力分析[J].天然气工业,2009,29(5):72-74. ZHU Huashu, YU Ruiqing, LIAO Zhonghui, et al. Finite element analysis on rock stress status during gas drilling deviation[J]. Natural Gas Industry, 2009,29(5):72-74.

[8] ZHANG H, ZHANG H, GUO B, et al. Analytical and numerical modeling reveals the mechanism of rock failure in gas UBD[J]. Journal of Natural Gas Science and Engineering, 2012,4(3):29-34.

[9] 李士斌,窦同伟,董德仁,等.欠平衡钻井井底岩石的应力状态[J].石油学报,2011,32(2):329-334. LI Shibin, DOU Tongwei, DONG Deren, et al. Stress state of bottom hole rocks in underbalanced drilling[J]. Acta Petrolei Sinica, 2011,32(2):329-334.

[10] 李玮,闫铁,毕雪亮,等.欠平衡井底附近岩石应力状态分析[J].科学技术与工程,2012,20(21):5139-5143. LI Wei, YAN Tie, BI Xueliang, et al. Sdudy of rock stress state near the bottom to underbalance drilling[J]. Science Technology and Engineering,2012,20(21):5139-5143.

[11] 仉洪云,高德利,郭柏云.气体钻井井底岩石热应力分析[J].中国石油大学学报(自然科学版),2013,37(1):70-74. ZHANG Hongyun, GAO Deli, GUO Boyun. Thermal stress analysis on bottom hole rock in gas drilling[J]. Journal of China University of Petroleum(Edition of Natural Science),2013,37(1):70-74.

[12] 常德玉,李根生,黄中伟,等.井底压差对垂直井井底应力场的影响研究[J].岩土力学,2011,32(2):356-362. CHANG Deyu, LI Gensheng, HUANG Zhongwei, et al. Study of effect of bottom hole differential pressure on vertical well bottom hole stress field[J]. Rock and Soil Mechanics,2011,32(2):356-362.

[13] 常德玉,李根生,黄中伟,等.考虑三向地应力差时不同钻井条件下井底应力场研究[J].岩土力学,2011,32(5):1546-1552. CHANG Deyu, LI Gensheng, HUANG Zhongwei, et al. Study of bottom hole stress field with differential pressure of 3D in-situ stress under different drilling conditions[J]. Rock and Soil Mechanics, 2011,32(5):1546-1552.

[14] 常德玉,李根生,沈忠厚,等.深井超深井井底应力场[J].石油学报,2011,32(4):697-703. CHANG Deyu, LI Gensheng, SHEN Zhonghou, et al. The stress field of bottom hole in deep and ultra-deep wells[J]. Acta Petrolei Sinica, 2011,32(4):697-703.

[15] CHANG D, LI G, SHEN Z, et al. A study on the effect of bottom-hole differential pressure on the rock stress field[J]. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 2014,36(3):275-283.

[16] ZHU Y W, CAI Y Q, XU H. ABAQUS and analyses of rock engineering [M]. Hong Kong: The Chinese Book Publishing House, 2005.

[17] CAI M F, HE M C, LIU D Y. Rock mechanics and engineering [M]. Beijing: Science Press, 2002.

[18] 陈勉,金衍,张广清.石油工程岩石力学[M].北京:科学出版社,2008.

(编辑 李志芬)

A coupled thermo and poro-elastoplasticity analysis of stress distribution in bottom-hole rocks during drilling

ZHU Xiaohua, LIU Weiji

(SchoolofMech-ElectricalEngineeringinSouthwestPetroleumUniversity,Chengdu610500,China)

The stress distribution in bottom-hole rocks plays a key role on drilling efficiency. In this study, a fully coupled numerical simulation model was established, and the effects of overburden pressure, horizontal in-situ stresses, drilling fluid pressure, pore pressure and temperature on the stress distribution in bottom-hole rocks were investigated. The simulation results show that the maximum principle stress of the bottom-hole rock increases with the increasing of drilling fluid pressure, well depth and temperature difference, and it firstly increases and then decreases with the decrease of the permeability coefficient of the rock formation. In the axial direction of the well and under the bottom-hole surface, the maximum principle stress of the rocks decreases with the increase of drilling fluid pressure and well depth, while the temperature difference has little influence on it when the distance from the bottom hole surface reaches a certain value.

thermo and poro-elastoplasticity; bottom-hole rock stress; fully coupled; numerical solution; fragmentation mechanism

2015-10-26

国家自然科学基金项目(51222406,51674214)；四川省科技计划国际合作项目(2016HH0008)；四川省青年科技创新研究团队项目(2014TD0025)

祝效华(1978-)，男，教授，博士，博士生导师，研究方向为管柱力学和钻井提速。E-mail:zxhth113@163.com。

1673-5005(2016)05-0072-07

10.3969/j.issn.1673-5005.2016.05.008

TE 242

:A

祝效华,刘伟吉. 热孔弹塑性完全耦合作用下的井底岩石应力分布[J]. 中国石油大学学报(自然科学版),2016,40(5):72-78.

ZHU Xiaohua, LIU Weiji. A coupled thermo and poro-elastoplasticity analysis of stress distribution in bottom-hole rocks during drilling[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(5):72-78.