一微地震逆时聚焦定位算法的模拟实验研究

李 萌, 陶 果, 王 华, 李军孝

(中国石油大学油气资源与探测国家重点实验室,北京 102249)



一微地震逆时聚焦定位算法的模拟实验研究

李 萌, 陶 果, 王 华, 李军孝

(中国石油大学油气资源与探测国家重点实验室,北京 102249)

微地震事件的位置可由波动方程逆时聚焦获得,然而在实际应用中稀疏或有缺陷的观测系统会对定位结果产生较大影响,导致定位结果可能存在偏差及假象。提出以峰值信噪比和定位椭球半轴长作为定量评价定位结果清晰度与精度的新标准。通过地面与井下监测的模拟算例综合考察波形加载方式、成像条件、接收器密度、覆盖范围及多震源对定位结果的影响,并以此指导实际的微地震数据采集方案。模拟实验结果表明,混合逆时聚焦可调整定位精度与计算量,是一种较为灵活的波形加载方式;多尺度互相关成像条件具有较高的精度与分辨率,可满足实际定位需求;逆时聚焦定位结果的分辨率与精度分别取决于接收器密度与覆盖范围;由于多震源的互相干涉,分辨多震源需要更苛刻的采集条件。

微地震; 逆时聚焦定位; 峰值信噪比; 成像条件; 多震源

近年来,微地震监测被广泛地应用于油藏监测、煤矿开采、地热开发和非常规油气藏压裂增产等领域[1]。通过微地震事件的空间和时间分布可以估算地下的应力变化、渗流通道及诱导裂缝的几何产状,以此优化生产开发方案或进行地质灾害预警[2-3]。传统的地震定位方法需要拾取清晰可靠的初至[4-5],对信号的信噪比要求较高,然而实际采集的微地震数据普遍具有强噪声干扰,限制了这类定位方法的应用。适用于低信噪比数据的偏移类微地震定位方法[6-8]在最近十年成为了研究热点。其中具有代表性的工作包括McMechan[9]和Drew[10]借鉴逆时偏移原理,利用有限差分或相移法进行波场的逆时延拓,并认为使波场幅度达到最大的网格点与时间步长对应为震源的位置和起震时刻。随后,逆时聚焦定位算法得到了诸多改进和发展。Artman[11]利用纵、横波波场的互相关成像同时得到了震源的位置及能量辐射特性。Witten与Artman[12]基于噪声和信号逆时延拓波场的差异建立合适的阈值模型提高定位成像的质量。Haldorsen 等[13-14]利用反褶积提高了逆时聚焦定位结果的分辨率。Zhu[15]对逆时延拓的波场进行振幅补偿使得该算法的使用假设从弹性介质拓宽到了黏弹性介质。Nakata[16]和Sun[17]将接收器阵列分成几个子阵列,分别对各个子阵列逆时延拓的波场进行互相关叠加,提高了定位成像的分辨率。Li[18]将双树复小波变换与逆时聚焦定位相结合,增强了算法的抗噪性与分辨率。在实际应用中受稀疏或有缺陷观测系统的影响,逆时聚焦定位算法的结果往往存在偏差或假象。另外,逆时聚焦定位算法的诸多改进方案有各自的优缺点及适用范围,对定位结果会产生较大影响。笔者提出以峰值信噪比(peak signal to noise ratio)和定位椭球半轴长作为定量评价定位结果清晰度与精度的新标准,对微地震逆时聚焦定位算法进行系统的模拟实验研究,定量考察不同的波形加载方式和成像条件对定位结果的影响,并从中选取一种符合实际定位需求的算法实现形式,综合考察接收器密度和覆盖范围对定位结果的影响并以此指导实际的微地震数据采集方案。

1 微地震逆时聚焦定位原理

1.1 逆时聚焦定位算法

波场互易原理和波动方程在非耗散介质中的时不变性为逆时聚焦定位算法的前提,即震源到接收器的格林函数与接收器到震源的格林函数完全相同[15]。该算法以实际观测的波形数据作为震源子波逆时加载在各个接收器,通过有限差分或相移法等数值方法重构逆时传播的波场,再施加一定的成像条件即可获得震源的位置。常规的成像条件是比较不同时刻的波场幅度,使波场幅度达到最大的时刻和位置为推定震源的起震时刻与震源位置[7]。

以2维弹性波方程为例,逆时传播的波场可表示为

(1)

式中,d为实际观测到的波形数据;T为总的记录时间;x和z为空间坐标;λ和μ为拉梅系数;ρ为介质密度;u为逆时外推的波场。震源的位置(x0,z0)和起震时刻t0可由下式得出:

(x0,z0,t0)=max[u(x,z,t)].

(2)

为了得到完整的震源信息,逆时加载的波形应包含整个有效事件。另外,由于速度模型存在一定误差,为了保证逆时传播的能量能够最终收敛,波动方程逆时延拓的时长可选为实际加载波形长度的2倍。图1为接收器布置在地表(z=0)不同时刻的逆时波场快照。当波场传播到震源的起震时刻(t=0 ms)时,波场能量会聚焦到真实的震源位置。受实际采集条件的限制,震源附近完整的采样信息难以得到,导致逆时定位的最终结果为一个椭圆而非一个点。该椭圆的半轴长给出了逆时聚焦定位的精度,提供了评价逆时聚焦定位结果的标准和依据。

1.2 逆时聚焦定位结果的评价标准

利用峰值信噪比、定位椭球半轴长σ以及与理论震源位置的定位误差作为定量评价逆时聚焦定位结果质量的标准。峰值信噪比(RPSN)是衡量定位结果是否清晰的度量,其值越高,逆时聚焦定位结果越清晰,越容易分辨震源的位置。峰值信噪比RPSN的具体定义由下式给出:

(3)

式中,x为空间坐标,在3维情况下x为(x,y,z);N为定位结果I中所有点的个数;Dn为I的一个子集,它由数值小于某个阈值的所有点构成,即n(x)=I(xx∈Dn),本文中所采用的阈值为峰值的一半。

3维逆时聚焦定位结果为一个椭球,该椭球在水平及垂直切片上投影的半轴长σx、σy和σz可以作为该算法的定位精度。半轴长越大,说明定位结果的精度越低。

图1 逆时延拓的波场在不同时刻的波场快照

逆时聚焦定位在垂直方向的概率密度分布函数pz的计算公式为

(4)

式中,Ixz为成像函数在x-z平面的切片;Nz和Nx分别为z和x方向的空间采样点数。

垂直方向的定位精度σz为

σz=[max(zc)-min(zc)]/2.

(5)

除峰值信噪比RPSN和定位精度σ外,反演震源位置与理论震源位置的绝对误差为衡量定位结果质量的第3个参数:Error=x-x0。

图2 逆时聚焦定位椭球与定位精度示意图

2 波形加载方式与成像条件对逆时聚焦定位结果的影响

2.1 波形加载方式

与逆时偏移类似,在逆时聚焦定位算法中常规的波形加载是一次完成的[6]:

(6)

式中,u为逆时传播的波场;Nr为接收器总数;Ri为第i个接收器的波形。这种加载方式将各个接收器产生的外推波场的累加值作为最终的逆时波场。

Nakata[16]对每个接收器的波场进行独立的逆时传播,将这些子波场的乘积作为最终的逆时波场:

(7)

Sun[17]将以上两种方式进行组合,得到了混合的波形加载方式:

(8)

式中,n为接收器局部累加的个数,其本质是公式(6)和(7)的组合。核心思想是先将接收器阵列分为几个子阵列,对每个子阵列中的接收器波形进行累加,再将所有子阵列波场的乘积作为最终逆时传播的波场。为了方便描述,公式(6)～(8)所代表的加载方式分别简称为累加逆时聚焦(SRTM)、乘积逆时聚焦(MRTM)和混合逆时聚焦(HRTM)。

图3为数值试验的纵波速度模型,纵横波速度比为1.8,密度为2.4 g/cm3,接收器位于地表,震源位于模型中间。通过2维四阶交错有限差分[19-21]获得正向和反向传播的波场,模型为201 m×201 m×201 m,网格间距为1 m,时间采样间隔为10-4s,震源为Ricker子波,主频100 Hz,记录时长为0.3 s。

图4(a)～(c)为SRTM、MRTM和HRTM的定位结果。由于接收器分布比较稀疏,SRTM的结果在距离接收器较近的区域有明显的成像噪声,另外

还存在较强的旁瓣干扰,该旁瓣可能来自震源附近散射能量的叠加,而MRTM仅在震源附近有较强的能量分布,HRTM的结果则处在SRTM和MRTM之间。为了定量评价定位结果的质量,3种波形加载方式的峰值信噪比、定位精度以及与理论震源位置的定位误差分别如图4(d)～(f)所示。

图3 速度模型

图4 SRTM、MRTM和HRTM的逆时聚焦定位结果及对应的峰值信噪比、定位精度和定位误差

由图可知MRTM的峰值信噪比最高、定位精度最小,说明该方法的定位结果最清晰且定位精度最高,HRTM次之,SRTM最低。但是,SRTM同时加载所有接收器的波形,所以只需一次逆时传播,而MRTM是各个接收器独立加载,总共需要Nr次逆时传播,与之类似,HRTM总共需要Nr/n次。由此可见,HRTM是一种较为灵活的、能够权衡定位精度与计算量的波形加载方式。

2.2 成像条件

常规逆时聚焦定位的成像条件需要在一定的时窗范围内搜索逆时延拓波场的幅度极值。然而,稀疏的观测阵列使得接收器附近的逆时波场具有较大的幅度,难以确定真实震源的位置,因此需要探索更为合适的成像条件。Steiner[22-23]提出以逆时延拓波场的模在时间上的积分作为成像条件,以此来消除时间轴,得到只与坐标相关的定位结果。该成像能量最大的网格点为推定震源的位置,使震源附近波场能量最大的时刻即为起震时刻:

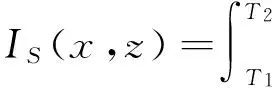
(9)

(x0,z0)=max(I), t0=max(I(V)).

(10)

式中,|u|为逆时波场的模;T1和T2为起始时刻和终止时刻;I为成像函数;V为震源位置附近的邻域。

Artman[11]将逆时传播的远场波场分离为纵、横波,定位结果为纵波和横波波场乘积在整个时间上的积分:

IPS=∫tP(x,z,t)S(x,z,t).

(11)

式中,IPS为最终的定位成像结果,纵横波波场可通过位移场的散度和旋度求得[24-25]。

为了提高逆时聚焦定位的分辨率及抗噪性,Li[18]基于双树复小波变换,将实际接收到的波形数据进行多尺度展开,并在不同尺度上分别进行逆时聚焦定位,最终的定位结果为有效尺度结果的乘积:

(12)

(13)

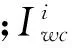
采用与2.1节相同的模型设置,对比上述3种成像条件的结果。为便于描述,用I_S、I_PS、I_M代表公式(9)、(11)、(13)所对应的成像条件。

图5(a)～(c)和图5(d)～(f)分别为垂直点力源和水平点力源的I_S、I_PS和I_M的逆时聚焦定位结果。

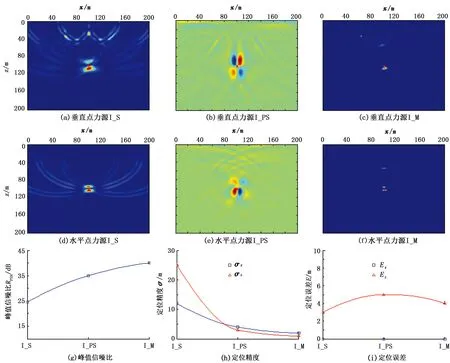
图5 垂直和水平点力源的I_S、I_PS、I_M的逆时聚焦定位结果及垂直点力源对应的峰值信噪比、定位精度和定位误差

对于I_S和I_M来说,成像能量最大点为震源位置,且震源性质的改变没有对定位结果产生较大影响。I_PS的定位结果则为“四片花瓣”,震源为“四片花瓣”的中点。对垂直点力源,“花瓣”主对角线方向为成像能量极小值,副对角线方向为成像能量极大值;对水平点力源,“花瓣”的左边为成像能量的正向极大值,右边为成像能量的极小值,说明I_PS不仅能给出震源位置,还能展现震源的能量辐射特性。图5(g)～(i)分别为垂直点力源3种成像条件的峰值信噪比、定位精度以及定位误差。由图可知,3种成像条件的定位结果与理论震源的误差较为接近。另外,I_M的结果有更高的分辨率和定位精度,这是多个尺度互相关的结果。

3 数据采集方案对逆时聚焦定位的影响

除了波形加载方式和成像条件,在实际应用中接收器的分布也会对逆时聚焦定位结果产生较大影响。基于3维模拟数据具体探讨接收器的密度与覆盖范围对逆时聚焦定位结果的影响,并以此作为实际数据采集方案的设计依据。试验采用与2.1节相同的层状速度模型,模型大小为201 m×201 m×201 m,网格间距为0.5 m,时间采样间隔为5×10-5s,记录时长为0.12 s,震源子波采用主频为150 Hz的雷克子波。

3.1 接收器的密度

图6为地面(图6(a)～(c))和井下(图6(d)～(f))的6种采集方案,蓝色三角为接收器,模型中间的红星为预设的震源。地面和井下采集方案的接收器个数大致相当,以此对比二者定位结果的异同。

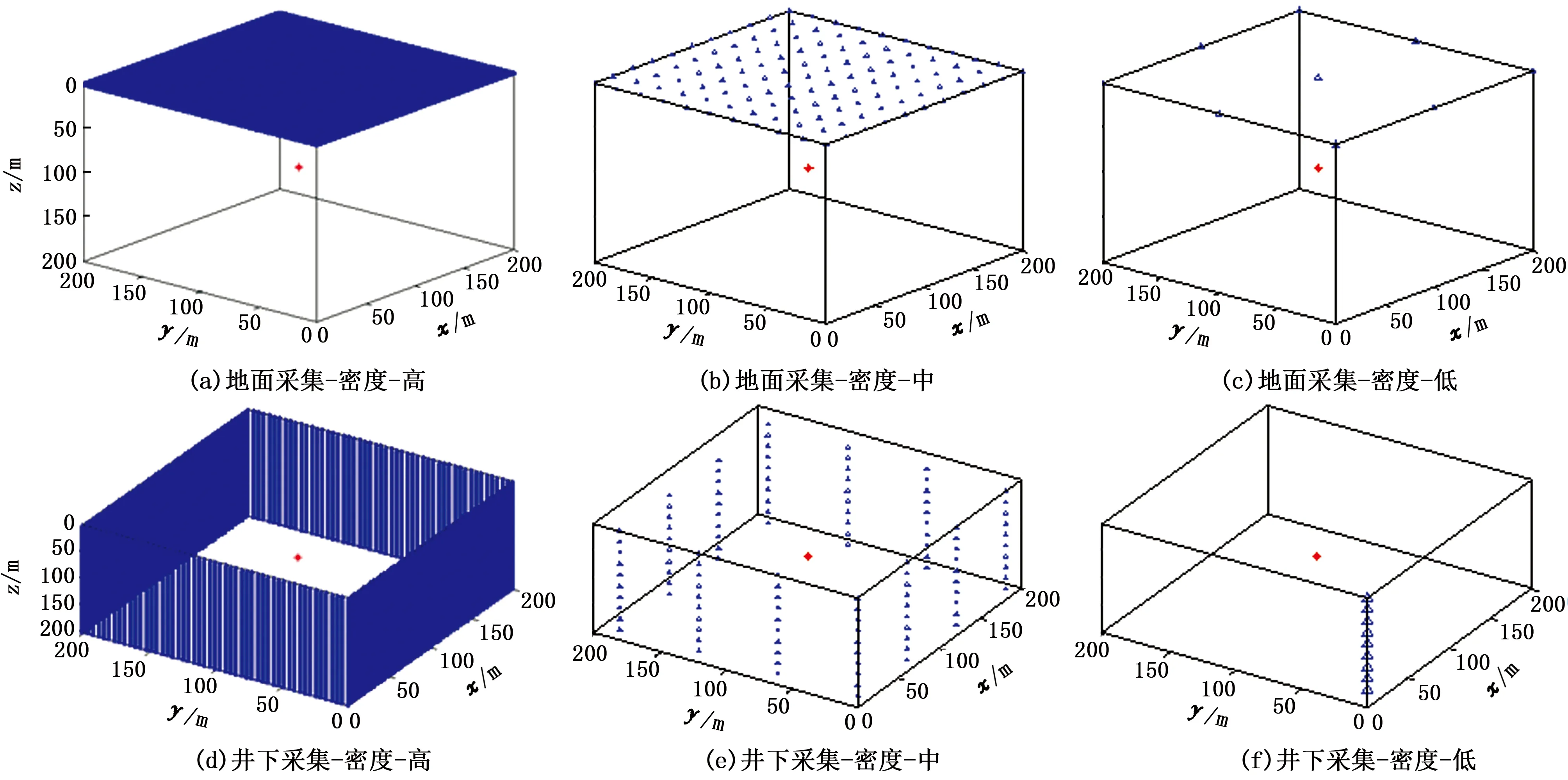
图6 地面与井下的接收器密度试验采集方案

图7和图8分别为地面和井下定位结果的x-y和x-z切片图。由图可知,随着接收器密度的降低,定位结果逐渐受到成像假象的干扰。另外,由于单垂直井监测缺少对震源方位的约束,其定位结果在x-y切片上呈现出以接收器阵列为圆心,以接收器到震源距离为半径的圆弧。图9为不同采集方案的峰值信噪比、定位精度以及与理论震源位置的定位误差。其中,xyS、xzS、yzS和xyD、xzD、yzD分别为地面和井下采集x-y切片、x-z切片和y-z切片的峰值信噪比;σx_S、σy_S、σz_S和σx_D,σy_D、σz_D分别为地面和井下采集x、y、z方向的定位精度;Errorx_S、Errory_S、Errorz_S和Errorx_D、Errory_D、Errorz_D分别为地面和井下采集x、y、z方向的定位误差。

由图可知:①由于缺乏深度约束地面采集横向切片的峰值信噪比高于x-z和y-z切片,而井下采集则正好相反。另外,地面和井下的峰值信噪比都随着接收器密度的减小而降低。②地面采集的x和y方向定位精度高于z方向,而井下采集3个方向的定位精度相差不大,这是因为多口井的方位约束提高了x和y方向的精度。另外,定位精度几乎不随着接收器密度的减小而变化。③除了单垂直井监测,地面与井下监测的定位误差不随着接收器密度的降低而增大。

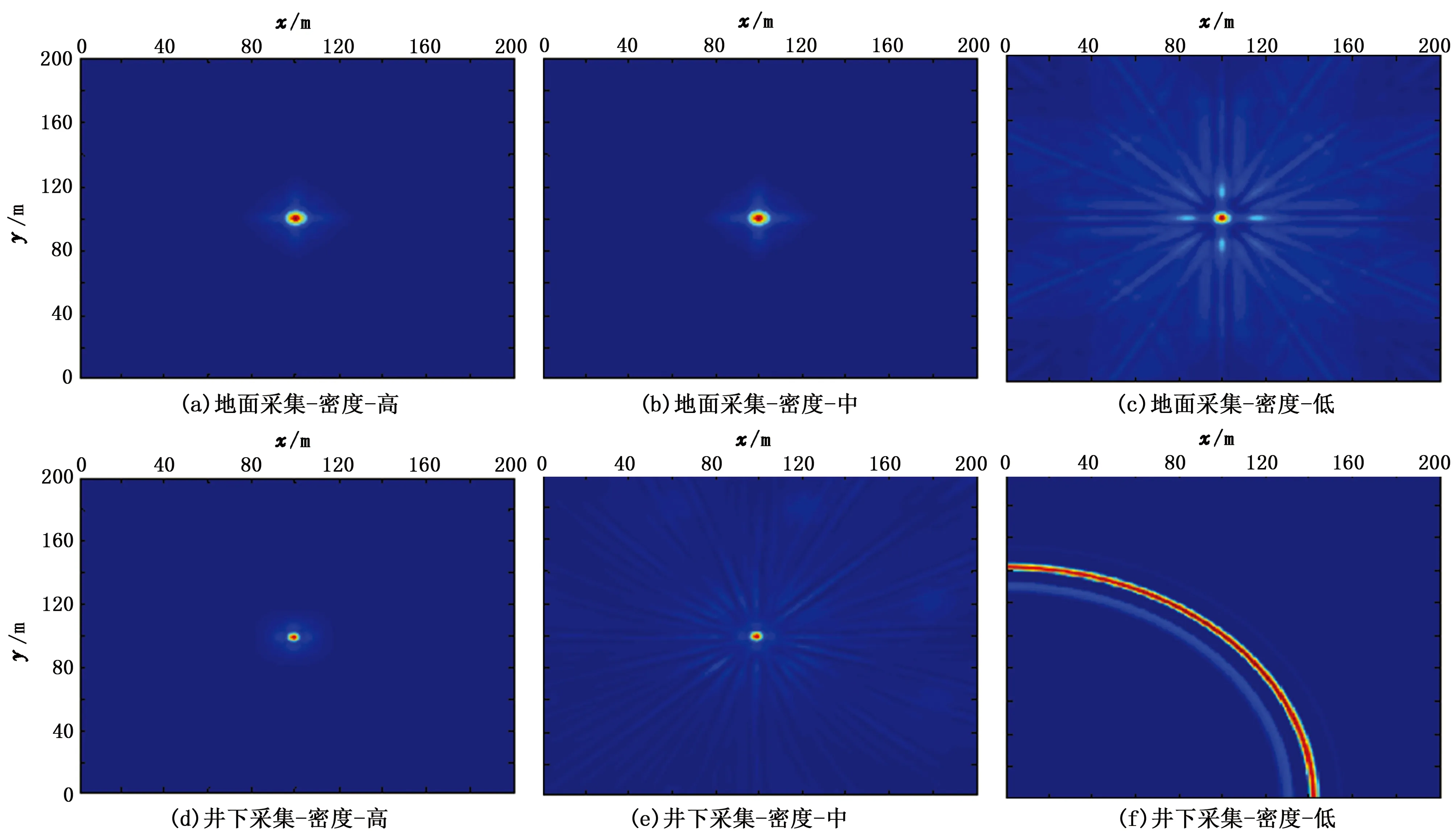
图7 地面与井下3种采集方案定位结果的x-y切片

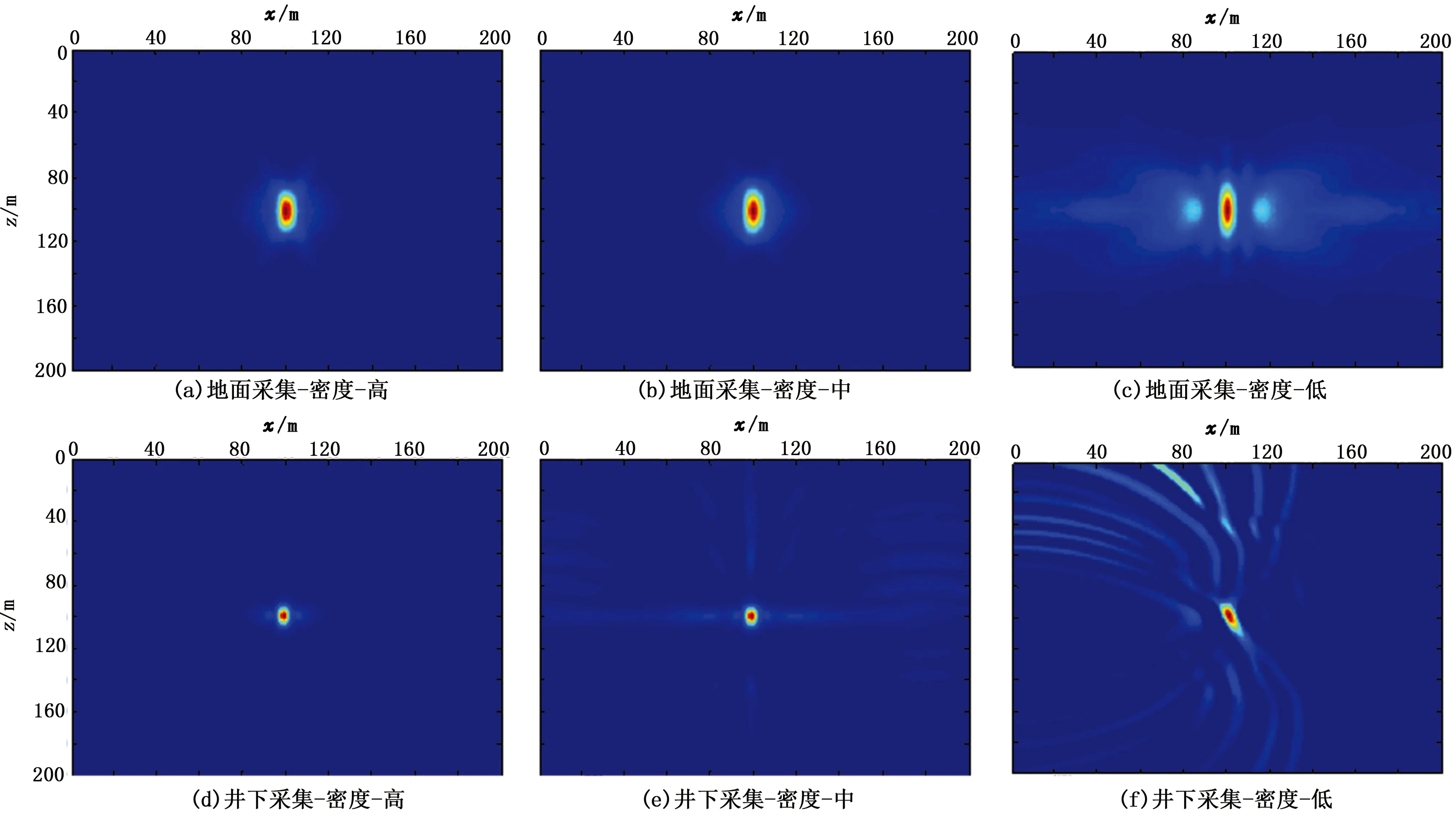
图8 地面与井下3种采集方案定位结果的x-z切片

图9 地面与井下监测的峰值信噪比、定位精度和定位误差

3.2 接收器的覆盖范围

考察接收器覆盖范围对逆时聚焦定位结果的影响。图10为地面(a)～(c)和井下(d)～(f)6种采集方案,除覆盖范围不同,其他参数保持一致。为比较地面和井下定位结果的差异,二者的接收器个数和地面覆盖范围大致对应相同。

图11～13分别为地面和井下定位结果的x-y、x-z切片和不同采集方案的峰值信噪比、定位精度及与理论震源位置的定位误差。由图可知:①对于地面采集,3个平面的峰值信噪比随着接收器覆盖面积的下降而降低;而对于井下采集,3个平面的峰值信噪比相差不多且不随着接收器地面覆盖范围的降低而产生较大的变化。②对于地面采集,3个方向的定位精度随着接收器地面覆盖面积的降低而降低;而对于井下采集,定位精度基本相同并且基本不随着接收器覆盖面积的减小而变化。这说明对多井监测来说,垂直方向的覆盖深度对定位结果的贡献更大。

图10 地面与井下的接收器覆盖范围试验采集方案

图11 地面与井下3种采集方案定位结果的x-y切片

图12 地面与井下3种采集方案定位结果的x-z方向切片

图13 地面与井下的峰值信噪比、定位精度和定位误差

4 基于逆时聚焦定位多震源的可能性分析

在实际的微地震监测中,震源往往成簇状分布,即在较短时间内产生多个距离很近的微地震事件。为了测试逆时聚集定位对多个震源的分辨率,设计如下试验(图14)。图中红星代表5×5个震源,震源的间距为一个波长(约30 m)以保证算法有足够的分辨能力,震源具有相同的起震时刻(0 s),深度位于模型中间,接收器设置与3.1节相同。

图14 地面与井下的多震源试验采集方案

图15和图16为多震源定位结果的x-y和x-z切片。由图可知:①由于单井监测缺乏x和y方向的约束能力,其x-y平面的定位结果呈现出多个圆弧(各个震源到接收器阵列的半径各不相同)。②当采集阵列理想时,逆时聚焦定位可以准确地得到各个微震事件的位置。③多震源对接收器密度要求更高,相同的接收器分布可以在单震源试验中得到准确的结果(图7(e)和图8(e)),却无法在多震源试验中取得成功(图15(e)和图16(e))，这是因为多个事件的逆时波场互相干涉叠加,对各自的定位结果造成干扰。④尽管存在较强的干扰,图14(b)中的采集方案仍然可以准确地辨别各个震源的位置，其接收器的间隔正好是微震事件的一个波长,这说明只有在接收器间隔小于微震事件一个主波长的情况下,逆时聚焦定位算法才能得到多个震源的准确位置。

图15 地面与井下采集方案的多震源定位结果x-y切片

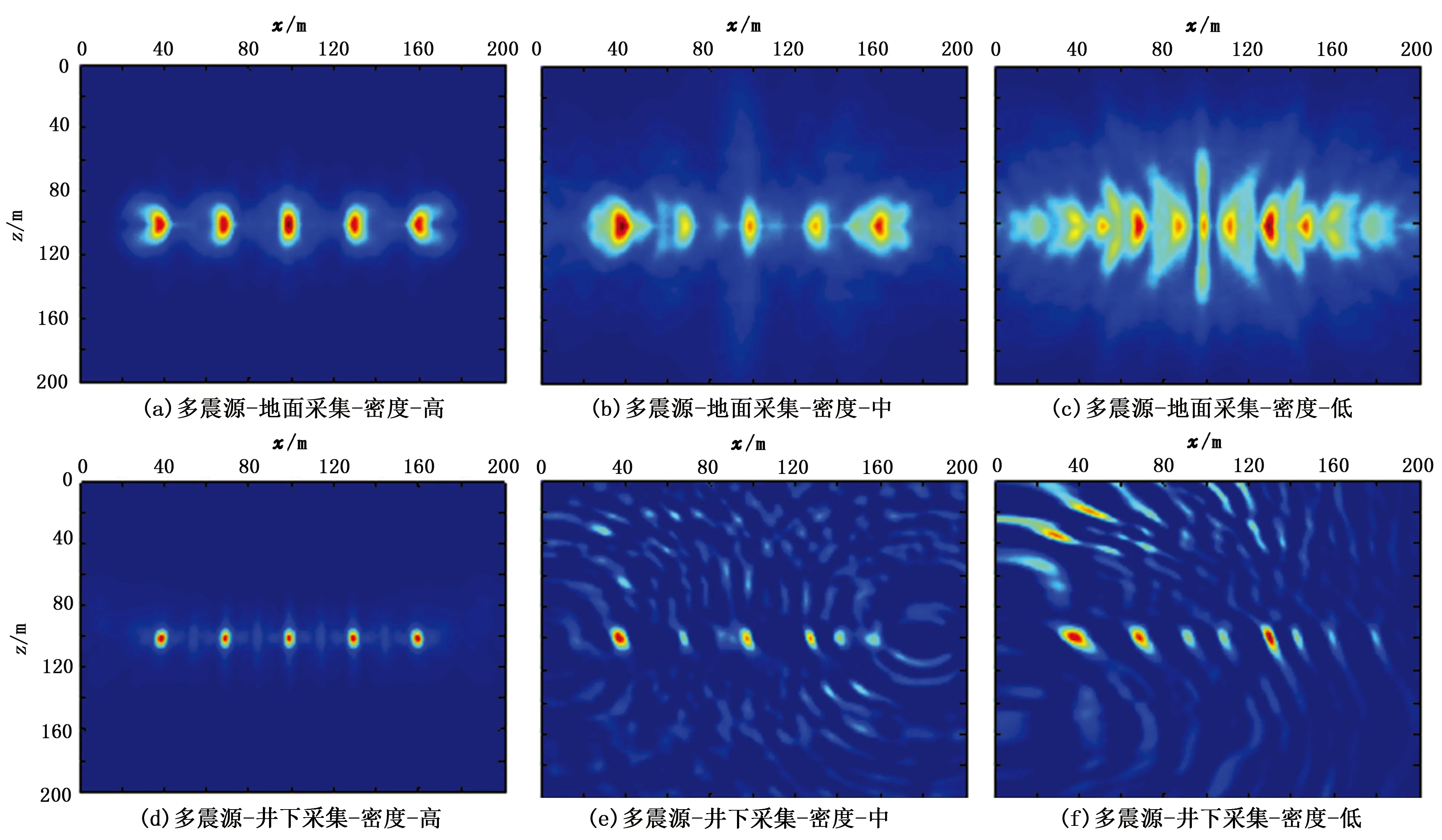
图16 地面与井下采集方案的多震源定位结果x-z方向切片

5 结果讨论

本文中基于模拟数据对微地震逆时聚焦定位进行了系统的模拟实验研究。首先,提出以峰值信噪比和定位椭球半轴长作为定量评价定位结果清晰度与精度的新标准。其次,对比了不同的波形加载方式和成像条件对定位结果的影响,得到了各自的优缺点及适用范围。最后,综合考察了地面与井下不同的接收器密度、接收器覆盖范围以及多震源对定位结果的影响，并以此指导实际微地震数据采集方案的设计。基于数值算例及分析,发现逆时聚焦定位的关键是获取震源附近足够多的采样信息。然而,3维逆时聚焦定位算法需要大量的计算量延拓逆时波场，定位过程耗时很长,该方法暂时仅适合后期的数据处理及分析而非实时定位。未来需要研究逆时聚焦定位的高性能并行算法及GPU加速实现。另外,本文中没有考虑速度模型的各向异性以及地层衰减对定位结果的影响,这也是值得未来深入研究的方向。

6 结 论

(1)混合逆时聚焦(HRTM)是一种较为灵活的,可调整定位精度与计算量的波形加载方式。

(2)纵横波能量互相关成像条件可揭示震源的辐射特性,但有很强的旁瓣干扰,不易确定震源的位置。多尺度互相关定位结果不受震源性质影响，并具有较高的定位精度与分辨率,可满足实际定位需求。

(3)接收器密度是决定定位成像结果清晰度的主要因素,而接收器覆盖面积则决定了定位精度。

(4)由于多震源的互相干涉,分辨多震源需要更苛刻的采集条件(接收器间距小于一个震源主波长)。

[1] MIYAZAWA M, VENKATARAMAN A, SNIEDER R, et al. Analysis of microearthquake data at cold lake and its applications to reservoir monitoring [J]. Geophysics, 2008,73(3):O15-O21.

[2] MAXWELL S C, RUTLEDGE J, JONES R, et al. Petroleum reservoir characterization using downhole microseismic monitoring [J]. Geophysics, 2010,75(5):A129-A137.

[3] WANG H, LI M, SHANG X F. Current developments on micro-seismic data processing [J]. Journal of Natural Gas Science & Engineering, 2016,32:521-537.

[4] GEIGER L. Probability method for the determination of ea- rthquake epicenters from arrival time only [J]. Bull St Louis Univ, 1912,8:60-71.

[5] LOMAX A, MICHELINI A, CURTIS A. Earthquake location, direct, global-search methods [M]. New York:Springer, 2009.

[6] FINK M. Time-reversed acoustics [J]. Scientific American, 1999,281(11):91-97.

[7] GAJEWSKI D, TESSMER E. Revere modeling for seismic events characterization [J]. Geophysical Journal International, 2005,163:276-284.

[8] RENTSCH S, BUSKE S, LUTH S, et al. Fast location of seismicity: a migration-type approach with application to hydralic-fracturing data [J]. Geophysics, 2007,72(1):S33-S40.

[9] MCMECHAN G. Determination of source parameters by wavefield extrapolation[J]. Geophysical Journal of the Royal Astronomical Society, 1982,71:613-628.

[10] DREW J, LESLIE D, ARMESTRONG P. Automated mi- croseismic event detection and location by continuous spatial mapping[R].SPE 95513, 2005.

[11] ARTMAN B, PODLADTCHIKOV I, WITTEN B. Source location using time-reverse imaging [J].Geophysical Prospecting, 2010,58:861-873.

[12] WITTEN B, ARTMAN B. Signal-to-noise estimates of time-reverse images [J]. Geophysics, 2011,76(2):MA1-MA10.

[13] HALDORSEN J B U, MILENKOVIC M, BROOKS N, et al. Locating microseismic events using migration-based deconvolution [C/OL]//2012 SEG Annual Meeting. Las Vegas, Nevada, November 18-23: SEG Technical Program Expanded Abstracts, SEG-2012-0248: 1-5. [2015-04-12]. http://library.seg.org/doi/pdfplus/10.1190/segam2012-0248.1.

[14] HALDORSEN J B U, BROOKS N, MILENKOVIC M. Migration-based deconvolution for high resolution locating of microseismic sources from multi-component recordings [C/OL]//2013 Fourth EAGE Passive Seismic Workshop. Amsterdam, Netherlands, March 17-20: EAGE Technical Program Expanded Abstracts, PSP05. [2015-04-10]. http://earthdoc.eage.org/publication/publicationdetails/?publication=66883.

[15] ZHU T Y. Time-reverse modelling of acoustic wave propagation in attenuating media [J]. Geophysical Journal International, 2014,197(1):483-494.

[16] NAKATA N, GREGORY C B. Reverse-time migration for microseismic sources using the geometric mean as an imaging condition [C/OL]//2015 SEG Annual Meeting. New Orleans, Louisiana, October 18-23: SEG Technical Program Expanded Abstracts, SEG-2015-5851848: 2451-2455. [2015-10-30]. http://library.seg.org/doi/pdf/10.1190/segam2015-5851848.1.

[17] SUN J, ZHU T, FOMEL S. Investigating the possibility of locating microseismic sources using distributed sensor networks[C/OL]//2015 SEG Annual Meeting. New Orleans, Louisiana, October 18-23: SEG Technical Program Expanded Abstracts, SEG-2015-5888848: 2485-2490. [2015-10-30]. http://library.seg.org/doi/pdf/10.1190/segam2015-5888848.1.

[18] LI M, TAO G, WANG B, et al. Locating microseismic events with multi-scale time reversed imaging: a synthetic case study[C/OL]//2015 SEG Annual Meeting. New Orleans, Louisiana, October 18-23: SEG Technical Program Expanded Abstracts, SEG-2015-5860203: 2496-2500. [2015-10-30]. http://library.seg.org/doi/pdf/10.1190/segam2015-5860203.1.

[19] ZHANG K, TAO G, LI J X, et al. 3D FDM modeling of acoustic reflection logging in a deviated well [C/OL]//2014 EAGE Annual meeting. Amsterdam, Netherlands, June 16-19: EAGE Technical Program Expanded Abstracts, P10 03. [2014-12-24]. http://earthdoc.eage.org/publication/publicationdetails/?publication=76504.

[20] 方刚,FOMEL S,杜启振. 交错网格Lowrank有限差分及其在逆时偏移中的应用[J]. 中国石油大学学报(自然科学版), 2014,38(2):44-51. FANG Gang, FOMEL Sergey, DU Qizhen. Lowrank finite difference on a staggered grid and its application on reverse time migration [J]. Journal of China University of Petroleum (Edition of Natural Science), 2014,38(2):44-51.

[21] 王永刚,邢文军,谢万学,等.完全匹配层吸收边界条件的研究[J].中国石油大学学报(自然科学版),2007,31(1):19-24. WANG Yonggang, XING Wenjun, XIE Wanxue, et al. Study of absorbing boundary condition by perfectly-matched layer [J].Journal of China University of Petroleum(Edition of Natural Science), 2007,31(1):19-24.

[22] STEINER B. Time reverse modeling of low-frequency tremor signals [D]. Zurich: Swiss Federal Institute of Technology Zurich, 2008.

[23] STEINER B, SAENGER E H, SCHMALLHOLZ S M. Time reverse modeling of low-frequency microtremors: application to hydrocarbon reservoir localization [J]. Geophysical Research Letters, 2008, 35:L03307.

[24] MORSE P M, FESHBACH H. Methods of theoretical physics [M]. New York: McGraw-Hill Book, 1953.

[25] AKI K, RICHARDS P. Quantitative seismology [M]. Sausalito: University Science Books, 2002.

(编辑 修荣荣)

Parametric optimization on locating microseismic events with reverse time imaging

LI Meng, TAO Guo, WANG Hua, LI Junxiao

(StateKeyLaboratoryofPetroleumResourcesandProspectinginChinaUniversityofPetroleum,Beijing102249,China)

Microseismic events can be located using reverse time imaging method, which employs the full waveform data to back propagate to its real origin based on wave equation. However, the estimated locations are strongly dependent on various implementations of the method and the sparsity of sensor geometry, which may result in unreliable location estimations. In this paper, we introduce the peak signal to noise ratio and the semi-axis of the imaged ellipse as new standards to quantitatively evaluate the accuracy and precision of the algorithm. Subsequently, we select one reliable implementation which satisfies the requirement of real data processing based on the pros and cons of various image conditions and waveform input methods. We investigate the impact of density and coverage of receiver array as well as the multiple events on the locations results using synthetic examples and use the results to guide real microseismic data acquisition. The simulated analysis shows that hybrid reverse time imaging trades off between location accuracy and computational efficiency. Multi-scale reverse time imaging condition has better location accuracy and precision, which satisfies the requirement of real-time processing in microseismic field work. In addition, the location accuracy and precision are mainly dependent on the density and coverage of the receiver array, respectively. Finally, successful location of simultaneous multiple microseismic sources requires more rigorous acquisition plans due to the interferences between different events.

microseismic; event location with reverse time imaging;peak signal to noise ratio;image conditions; multiple microseismic sources

2016-04-11

国家自然科学基金项目(41174118，41204094)；中国石油大学(北京)科研基金项目(2462015YQ0506)

李萌(1988-)，男，博士研究生，研究方向为井孔地球物理及微地震震源定位。E-mail: limengxiaoliu@sina.com。

1673-5005(2016)05-0059-13

10.3969/j.issn.1673-5005.2016.05.007

P 631.4

: A

李萌,陶果,王华,等. 微地震逆时聚焦定位算法的模拟实验研究[J].中国石油大学学报(自然科学版), 2016,40(5):59-71.

LI Meng, TAO Guo, WANG Hua, et al. Parametric optimization on locating microseismic events with reverse time imaging[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(5):59-71.